Составляет (рис. 15)

1 составляет (рис. 15)

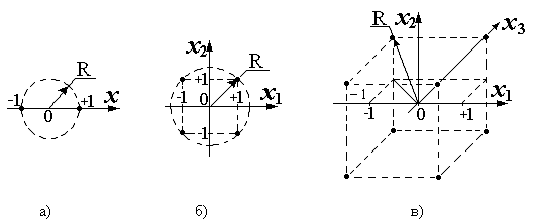
Рис. 15. Радиус окружности (сферы), на которой лежат точки плана ПФЭ 2n при диапазоне варьирования факторов от –1 до +1:

а) - n=1, ;

б) - n=2, ;

в) - n=3,

.

Таким образом, при построении РОЦКП с ядром из плана ПФЭ 2n плечо “звездных” точек определяется числом факторов

.

Раннее при определении параметров ортогонального композиционного плана второго порядка с ядром из плана ПФЭ 2n было получено

,

где - число точек плана ПФЭ,

- полное число точек композиционного плана второго порядка,

- константа преобразования элементов столбцов, соответствующих квадратам факторов.

В этом случае для РОЦКП число наблюдений в центре плана

.

Если n0 не целое, то при практическом построении плана его округляют до целого, но свойство ортогональности плана нарушается.

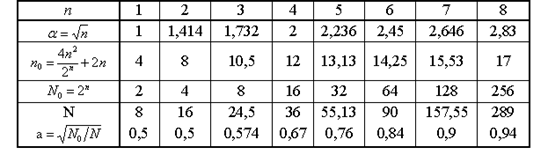
Параметры РОЦКП в зависимости от числа факторов

В [1] без вывода для РОЦКП рекомендуется принимать

.

Тогда

.

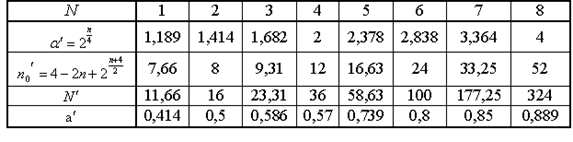
Параметры РОЦКП по [1]

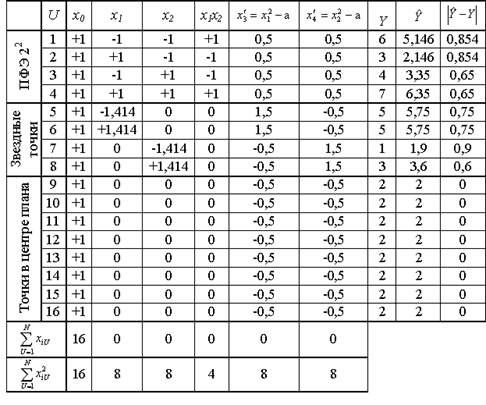
Пример рототабельного ортогонального центрально-композиционного плана для n = 2.

Параметры плана:

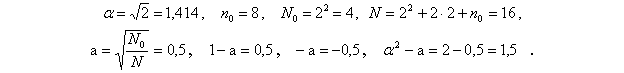
Нет необходимости проводить восемь раз (точки с 9 по 16) опыты в центре плана. Достаточно провести этот опыт один раз и записать результат во все восемь строк. Строки сокращать нельзя, так как нарушается свойство ортогональности, и коэффициенты полинома будут определены неверно.

Коэффициенты квадратичного полинома рассчитаются, как и ранее.

Использован рассмотренный ранее план ПФЭ 22 с добавленными опытами 5-16.

,

, ,

,

,

.

Полином принимает вид

.

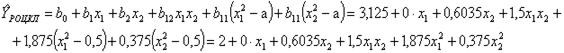Рассчитанные значения функции и расхождения с опытными данными представлены в предпоследнем и последнем столбцах плана.

Ранее для ОЦКП, при несколько отличающейся поверхности функции, был получен близкий полином в виде

.

Для n=2 число членов квадратичного полинома составляет шесть. В ОЦКП и РОЦКП необходимо провести девять отличающихся опытов при пяти уровнях варьирования факторов. Поэтому ОЦКП и РОЦКП - ненасыщенные планы. Такое число экспериментальных точек может быть использовано для построения, например, кубичных полиномов.

Лекция 9. Планы второго порядка с единичной областью планирования

Так как ОЦКП и РОЦКП - композиционные планы, то при естественной области планирования “звездные” точки могут выходить за пределы единичного гиперкуба и единичного гипершара. Для вписывания плана в область единичного гипершара необходимо изменить значение факторов путем умножения их на коэффициент

.

Так при ,

.

Значение факторов в ОЦКП и РОЦКП при переходе от естественной области планирования к единичному гипершару, при n = 2.

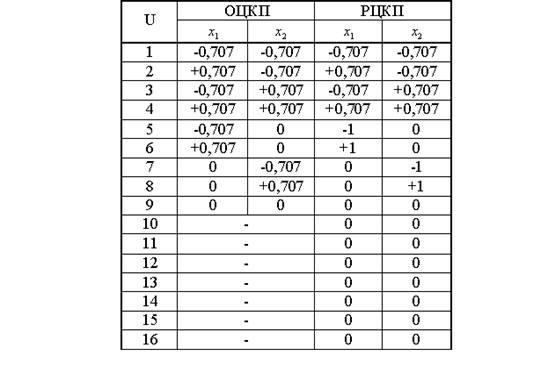
Могут использоваться рототабельные планы с точками плана в вершинах других, кроме квадрата (куба, суперкуба), правильных многогранников, вписанных в область единичного круга (шара, гипершара). В рототабельном плане на основе N0-угольника присутствуют N0 отличающихся точек на окружности, с радиусом R1=1, и n0 совпадающих точек в центре плана, с радиусом R2=0. При n=2 для квадратичного полинома при шести его членах число отличающихся точек плана должно быть не менее шести. В планах на основе пятиугольника (шестиугольника или семиугольника) присутствуют 6 (7 или 8) отличающихся точек, что меньше чем в ОЦКП и РОЦКП, у которых 9 отличающихся точек. При соответствующем выборе многоугольника можно сформировать насыщенный рототабельный план второго порядка. Значения факторов в точках плана определяются типом многоугольника.

Рототабельный план на основе правильного многоугольника при n=2.

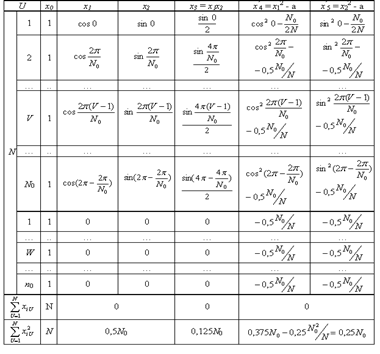
Константа преобразования элементов столбцов, соответствующих квадратам факторов, для всех подобных планов составляет

.

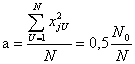Смотри, например, для столбцы i= 1 или 2 приведенного плана.

Соотношение может быть определено из уравнения выполнения условия ортогональности столбцов и

.

После несложных преобразований оно сводится к требованию

,

что выполняется при условии в таких планах

и следовательно N0=n0=0,5N .

Таким образом число точек в центре плана для всех подобных планов равно числу точек на поверхности единичного гипершара и определяется типом использованного многогранника.

Константа преобразования для всех подобных планов составляет а=0,25.

Например, в рототабельном плане при n=2 на основе правильного шестиугольника присутствуют 7 отличающихся точек: N0=6 точек на единичной окружности и n0=6 совпадающих точек в центре плана (рис. 16).

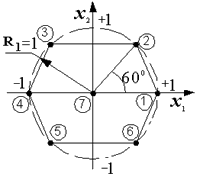
Рис. 16. Рототабельный план при n =2 на основе правильного шестиугольника

Здесь при построении плана первый фактор варьируется на пяти уровнях, а второй – на трех уровнях.

Рототабельный план при n=2 на основе шестиугольника

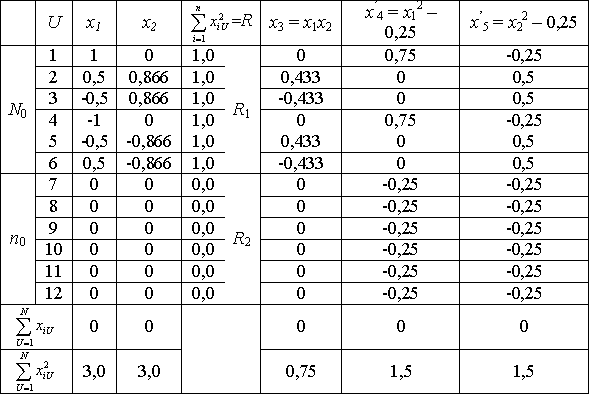
Существуют рототабельные планы, где оба радиуса не нулевые. При этом количество точек на каждой поверхности и отношение радиусов связаны.

Числа точек окружностей рототабельного плана и отношение их радиусов

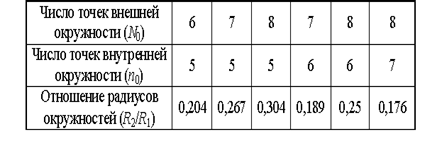
Пример такого плана при n=2, N0=8, n0=6, R2 / R1=0,25

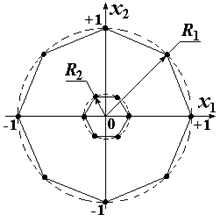
Рис. 17. Рототабельный план с двумя невырожденными окружностями.