В данной работе изложены основные принципы решения транспортной задачи, в частности ¾ задача о коммивояжере.
В работе использовано 5 источников, она содержит 29 страниц, 2 приложения, программу, написанную на языке Си.
Содержание
Реферат
Содержание
Введение
1.Постановка задачи о коммивояжере
2. Метод ветвей и границ
3. Использование верхних оценок
4. Решение с заданной точностью
Заключение
Список используемой литературы
Приложение 1
Приложение 2
Введение
Проблема оптимизации является в определенном смысле, пожалуй, самой острой проблемой современности. В любой сфере деятельности человек всегда ищет оптимальное решение.
Существует класс задач, которые не удовлетворяют принципу оптимальности, и, следовательно, для этих задач метод динамического программирования непосредственно использован быть не может. Их решение требует развития специальных способов последовательного анализа вариантов. В частности, к такому классу задач относится задача о коммивояжере (бродячем торговце).
Данная работа описывает нахождение оптимального решения задачи о коммивояжере, применяя метод ветвей и границ.
1.Постановка задачи о коммивояжере
Рассмотрим задачу о коммивояжере (бродячем торговце). Предположим, что бродячий торговец должен, покинув город, которому мы присвоим номер 1 (рис. 1), объехать еще N-1 городов и вернуться снова в город номер 1. В его распоряжении есть дороги, соединяющие эти города. Он должен выбрать свой маршрут - порядок посещения городов так, чтобы путь, который ему придется пройти, был как можно короче. Основное условие этой задачи состоит в том, что коммивояжер не имеет права возвращаться снова в тот город, в котором он однажды уже побывал. Это условие будем называть условием (a). Мы считаем, что расстояние между двумя городами - функция ![]() - определено. Разумеется, функция
- определено. Разумеется, функция ![]() может означать не только расстояние, но, например, время или издержки в пути и т. д. Поэтому в общем случае
может означать не только расстояние, но, например, время или издержки в пути и т. д. Поэтому в общем случае ![]()
![]() , а функции
, а функции ![]() естественно приписать значение ¥. Длина l пути S определяется формулой:
естественно приписать значение ¥. Длина l пути S определяется формулой:
![]() . (1)
. (1)
Сумма в выражении (1) распространена по всем индексам i и j, удовлетворяющим условию (a), т. е. условию, что каждый из индексов i и j входит в выражение (1) один и только один раз. Функция ![]() является, таким образом, аддитивной - она представима в виде суммы слагаемых, однако сама задача - задача отыскания минимума l - в силу ограничения (a) не является аддитивной и не удовлетворяет принципу оптимальности.
является, таким образом, аддитивной - она представима в виде суммы слагаемых, однако сама задача - задача отыскания минимума l - в силу ограничения (a) не является аддитивной и не удовлетворяет принципу оптимальности.

Рис.1.
Рассмотрим плоскость t, х, где t - дискретный аргумент, принимающий значения
0, 1, 2, . . . , N, соответствующие этапам путешествия бродячего торговца. Значение t=0 соответствует его начальному положению в городе номер 1, t - 1 - переходу из города номер 1 в город, который он выбрал первым для посещения, и т. д., t = N означает последний этап его путешествия - возвращение в город номер 1. Аргумент х теперь также принимает дискретные значения 1, 2,. . . , N (рис. 2). Соединим точку (0,1) с точками (1,1), (1,2), ..., (,1N) и длинам отрезков, соединяющих эти точки, припишем значения ![]() . Далее точки (1, s) - узлы, лежащие на первой вертикали, мы соединим со всеми узлами второй вертикали, длинам отрезков мы припишем значения
. Далее точки (1, s) - узлы, лежащие на первой вертикали, мы соединим со всеми узлами второй вертикали, длинам отрезков мы припишем значения ![]() и т. д. Точки (N-1, s) соединим с точкой (N, 1). В результате мы построили некоторый граф, каждая ломаная которого, соединяющая точку (0,1) с точкой (N, 1), описывает путь коммивояжера. Нашу задачу мы можем теперь сформулировать следующим образом. Среди всех ломаных, принадлежащих этому графу и соединяющих точки (0,1) и (N,1), и удовлетворяющих условию (a), найти ломаную кратчайшей длины. Условие (a) состоит теперь в том, что искомая ломаная пересекает (в узле) каждую из прямых х = i один и только один раз.
и т. д. Точки (N-1, s) соединим с точкой (N, 1). В результате мы построили некоторый граф, каждая ломаная которого, соединяющая точку (0,1) с точкой (N, 1), описывает путь коммивояжера. Нашу задачу мы можем теперь сформулировать следующим образом. Среди всех ломаных, принадлежащих этому графу и соединяющих точки (0,1) и (N,1), и удовлетворяющих условию (a), найти ломаную кратчайшей длины. Условие (a) состоит теперь в том, что искомая ломаная пересекает (в узле) каждую из прямых х = i один и только один раз.
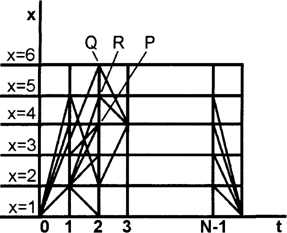
Рис. 2.
Рассмотрим узел Р, лежащий на третьей вертикали (см. рис. 2). Если бы условие (a) отсутствовало, то выбор траектории, которая соединяет точку Р с точкой (N, 1), не зависел бы от того пути, который привел нас в точку Р. В данном случае ситуация иная, и если два коммивояжера находятся в точке Р, но один из них пришел в это состояние, двигаясь вдоль траектории, проходящей через точку Q, а второй через точку R, то их состояния существенно отличаются друг от друга. Коммивояжер, который двигался по второй траектории, уже побывал в городах номер 2 и номер 5 и в будущем он уже не имеет права снова заезжать, в эти города. Что касается коммивояжера, который двигался вдоль первой траектории, то он побывал в городах номер 3 и номер 6; он не имеет права возвращаться в эти города, но зато он еще обязан посетить города номер 2 и номер 5 и т.д.
Поскольку функция ![]() определена на конечном множестве точек, то и функция
определена на конечном множестве точек, то и функция ![]() также определена на конечном множестве точек. Следовательно, задача определения минимума функции l сводится к перебору некоторого конечного множества значений этой функции, и проблема носит чисто вычислительный характер. Однако именно вычислительные трудности здесь огромны. Легко подсчитать, что число возможных вариантов (число значений функции l) равно (N-1)!. Таким образом, непосредственно перебрать и сравнить между собой все возможные пути, по которым может следовать бродячий торговец, для достаточно большого количества городов практически невозможно. Возникает проблема построения такого метода последовательного анализа вариантов, который выделял бы по возможности большое количество неперспективных вариантов и сводил задачу к перебору относительно небольшого количества "подозрительных" вариантов.
также определена на конечном множестве точек. Следовательно, задача определения минимума функции l сводится к перебору некоторого конечного множества значений этой функции, и проблема носит чисто вычислительный характер. Однако именно вычислительные трудности здесь огромны. Легко подсчитать, что число возможных вариантов (число значений функции l) равно (N-1)!. Таким образом, непосредственно перебрать и сравнить между собой все возможные пути, по которым может следовать бродячий торговец, для достаточно большого количества городов практически невозможно. Возникает проблема построения такого метода последовательного анализа вариантов, который выделял бы по возможности большое количество неперспективных вариантов и сводил задачу к перебору относительно небольшого количества "подозрительных" вариантов.
Основа этого, ныне широко распространенного метода состоит в построении нижних оценок решения, которые затем используются для отбраковки неконкурентоспособных вариантов.
Функция ![]() принимает конечное число значений
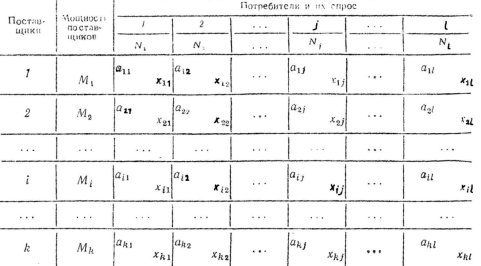
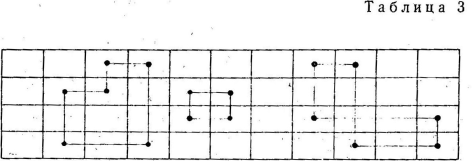
принимает конечное число значений ![]() , которые мы можем представить в виде таблицы (рис. 3). Предположим, что мы выбрали некоторый путь S
, которые мы можем представить в виде таблицы (рис. 3). Предположим, что мы выбрали некоторый путь S![]() . Его длина будет равна
. Его длина будет равна
![]() (2)
(2)
причем сумма (2) распространена по i, j так, что каждый из индексов встречается в ней один и только один раз. Величины ![]() с двумя одинаковыми индексами мы приняли равными ¥.
с двумя одинаковыми индексами мы приняли равными ¥.
Так как в каждый из вариантов s входит только один элемент из каждой строки и столбца, то мы можем проделать следующую операцию, которая здесь называется приведением матрицы. Обозначим через h![]() , наименьший элемент из строки номера i и построим новую матрицу C
, наименьший элемент из строки номера i и построим новую матрицу C![]() элементами
элементами
![]() .
.
Матрица C![]() определяет новую задачу коммивояжера, которая, однако, в качестве оптимальной будет иметь ту же последовательность городов. Между величинами
определяет новую задачу коммивояжера, которая, однако, в качестве оптимальной будет иметь ту же последовательность городов. Между величинами ![]() и
и ![]() будет существовать, очевидно, следующая связь:
будет существовать, очевидно, следующая связь:
![]()
Заметим, что в каждой из строк матрицы C![]() будет теперь, по крайней мере, один нулевой элемент. Далее обозначим через
будет теперь, по крайней мере, один нулевой элемент. Далее обозначим через ![]() наименьший элемент матрицы C
наименьший элемент матрицы C![]() , лежащий в столбце номера j, и построим новую матрицу С
, лежащий в столбце номера j, и построим новую матрицу С![]() с элементами
с элементами
![]()
Величины h![]() и
и ![]() называются константами приведения. Оптимальная последовательность городов для задачи коммивояжера с матрицей С
называются константами приведения. Оптимальная последовательность городов для задачи коммивояжера с матрицей С![]() будет, очевидно, такой же, как и для исходной задачи, а длины пути для варианта номера s в обеих задачах будут связаны между собой равенством
будет, очевидно, такой же, как и для исходной задачи, а длины пути для варианта номера s в обеих задачах будут связаны между собой равенством
![]() , (3)
, (3)
Где
![]() , (4)
, (4)
т.е. ![]() равна сумме констант приведения.
равна сумме констант приведения.
Обозначим через l * решение задачи коммивояжера, т. е.
![]() ,
,
где минимум берется по всем вариантам s, удовлетворяющим условию (a). Тогда величина ![]() будет простейшей нижней оценкой решения:
будет простейшей нижней оценкой решения:
![]() (5)
(5)
Будем рассматривать теперь задачу коммивояжера с матрицей С![]() , которую мы будем называть приведенной матрицей.
, которую мы будем называть приведенной матрицей.
Рассмотрим путь, содержащий непосредственный переход из города номера i в город номера j , тогда для пути s , содержащего этот переход, мы будем иметь, очевидно, следующую нижнюю оценку:
![]()
Следовательно, для тех переходов, для которых ![]() , мы будем иметь снова оценку (5). Естественно ожидать, что кратчайший путь содержит один из таких переходов - примем это соображение в качестве рабочей гипотезы. Рассмотрим один из переходов, для которого
, мы будем иметь снова оценку (5). Естественно ожидать, что кратчайший путь содержит один из таких переходов - примем это соображение в качестве рабочей гипотезы. Рассмотрим один из переходов, для которого ![]() , и обозначим через
, и обозначим через ![]() множество всех тех путей, которые не содержат перехода из i в j. Так как из города i мы должны куда-то выйти, то множество
множество всех тех путей, которые не содержат перехода из i в j. Так как из города i мы должны куда-то выйти, то множество ![]() содержит один из переходов i ® k, где k¹i; так как в город номера j мы должны прийти, то множество
содержит один из переходов i ® k, где k¹i; так как в город номера j мы должны прийти, то множество ![]() содержит переход т® i, где т¹ i. Следовательно, некоторый путь
содержит переход т® i, где т¹ i. Следовательно, некоторый путь ![]() , из множества
, из множества ![]() , содержащий переходы i ® k и т® i , будет иметь следующую нижнюю оценку:
, содержащий переходы i ® k и т® i , будет иметь следующую нижнюю оценку:
![]() .
.
Обозначим через
![]()
Тогда очевидно, что для любого ![]() множества путей
множества путей ![]() мы будем иметь оценку
мы будем иметь оценку
![]() (6)
(6)
Мы предполагаем исключить некоторое множество вариантов ![]() , поэтому мы заинтересованы выбрать такой переход i®j, для которого оценка (6) была бы самой высокой. Другими словами, среди нулевых элементов матрицы С
, поэтому мы заинтересованы выбрать такой переход i®j, для которого оценка (6) была бы самой высокой. Другими словами, среди нулевых элементов матрицы С![]() выберем тот, для которого
выберем тот, для которого ![]() максимально. Это число обозначим через
максимально. Это число обозначим через ![]() . Таким образом, все множество возможных вариантов мы разбили на два множества I
. Таким образом, все множество возможных вариантов мы разбили на два множества I![]() и I
и I![]() . Для путей из множества I
. Для путей из множества I![]() , мы имеем сценку (5). Для путей из множества I
, мы имеем сценку (5). Для путей из множества I![]() оценка будет следующей:
оценка будет следующей:
![]() . (7)
. (7)
Рассмотрим теперь множество I![]() , и матрицу С
, и матрицу С![]() . Так как все пути, принадлежащие этому множеству, содержат переход i®j, то для его исследования нам достаточно рассмотреть задачу коммивояжера, в которой города номеров i и j совпадают. Размерность этой задачи будет уже равна N - 1, а ее матрица получится из матрицы С
. Так как все пути, принадлежащие этому множеству, содержат переход i®j, то для его исследования нам достаточно рассмотреть задачу коммивояжера, в которой города номеров i и j совпадают. Размерность этой задачи будет уже равна N - 1, а ее матрица получится из матрицы С![]() вычеркиванием столбца номера j и строки номера i.
вычеркиванием столбца номера j и строки номера i.
Поскольку переход i®j невозможен, то элемент ![]() принимаем равным бесконечности.
принимаем равным бесконечности.
Рассмотрим случай N=3 (рис. 4, а) и предположим, что мы рассматриваем тот вариант, который содержит переход 3®2. Тогда задача коммивояжера после вычеркивания третьей строки и второго столбца вырождается в тривиальную. Ее матрица изображена на рис. 4, б). В этом случае мы имеем единственный путь, и его длина будет, очевидно, равна сумме
|
|
Итак, если в результате вычеркивания строки номера i и столбца номера j мы получим матрицу второго порядка, то задачу можно считать решенной.
Пусть теперь N > 3. После вычеркивания мы получим матрицу порядка N-1 >2. С этой матрицей (N-1)-го порядка совершим процедуру приведения. Матрицу, которую таким образом получим, обозначим через ![]() , а через
, а через ![]() - сумму ее констант приведения. Тогда для
- сумму ее констант приведения. Тогда для ![]() , мы будем иметь оценку
, мы будем иметь оценку
![]() . (8)
. (8)
На этом первый шаг алгоритма закончен. В результате одного шага мы разбили множество всех возможных вариантов на два множества ![]() , и для путей, принадлежащих этим множеством, мы получили оценки (8) и (7) (рис. 5).
, и для путей, принадлежащих этим множеством, мы получили оценки (8) и (7) (рис. 5).
|
![]()
![]()
Похожие работы
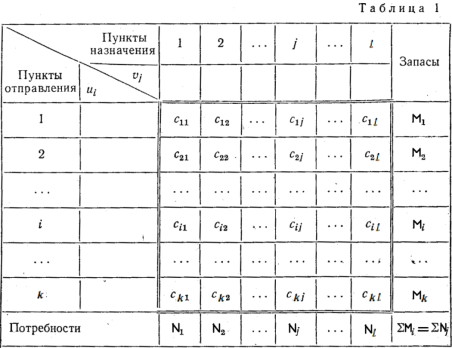
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... xij, удовлетворяющих поставленным ограничениям. Клетки с не нулевыми перевозками называются базисными, а с нулевыми – свободными. В зависимости от соотношения между запасами и заявками транспортная задача называется сбалансированной или несбалансированной. Сбалансированная ТЗ: Несбалансированная ТЗ: Для сбалансированной ТЗ ограничения принимают вид равенств, то есть получаем m+n ограничений, ...
... Аi к потребителю Bs определится как сумма значений пары соответствующих переменных: Дальнейший расчет будет выполнен с помощью венгерского метода решении транспортного алгоритма. 1.6 Решение транспортной задачи с ограниченными возможностями транспортных средств венгерским методом Предварительный этап. По исходной матрице С выполняется построение матрицы С', а затем матрицы Co, по ...
... ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение. 2. Содержательная постановка задачи Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения ...
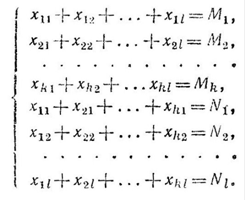

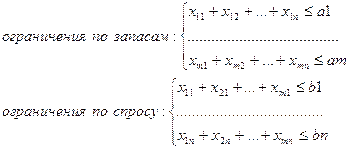

0 комментариев