Навигация
Юридический техникум Рассмотрено и одобрено ПЦК
г. Кропоткин программирования
Председатель ПЦК
Покалицына О.В.
План чтения лекции по учебной дисциплине
«Математические методы»
Раздел № 2. Линейное программирование. Тема № 2.5. Транспортная задача.
Место проведения: аудитория.
Литература:
1. Венцель Е.С. Исследование операций. Задач, принципы, методология. – М.: Наука, 1980.
2. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. – М.:ЮНИТИДАНА, 2001
Учебные вопросы и расчет времени
| №п/п | Учебные вопросы | Время, мин | Методические указания |
| 1. 2. 3. | Постановка транспортной задачи. Математическая модель транспортной задачи. Методы решения транспортной задачи. |
1. Вводная часть. Организационный момент. План занятия. Основные требования.
2. Основная часть.
1. Постановка транспортной задачи.
Важным частным случаем задачи линейного программирования является транспортная задача.
Постановка задачи: Пусть имеется m поставщиков и n потребителей. Мощность поставщиков и спросы потребителей, а так же затраты на перевозку груза для каждой пары «поставщик – потребитель» заданы таблицей.
| поставщики | потребители | В1 | В2 | … | Вj | … | Bn | Мощность поставщиков |
| A1 | С11 | С12 |
| С1j |
| С1n | a1 | |
| A2 | С21 | С22 |
| С2j |
| С2n | a2 | |
| … | … | … |
| … |
| … |
| |
| Ai | Сij | Сij |
| Сij |
| Сin | ai | |
| … | … | … |
| … |
| … |
| |
| Am | Cm1 | Cm2 |
| Cmj |
| Cmn | am | |
| Спрос потребителей | b1 | b2 |
| bj |
| bn |
| |
Найти объемы перевозок каждой пары «поставщик – потребитель» так, чтобы: мощности всех поставщиков были реализованы; спросы всех потребителей были удовлетворены; суммарные затраты на перевозку были бы максимальны.
Особенности математической модели транспортной задачи:
ü система ограничений есть система уравнений, то есть задача ЛП в каноническом виде;
ü коэффициенты при неизвестных системы ограничений равны единицы или нулю;
ü каждая переменная входит в систему ограничений два раза: один раз в систему ограничений поставок, второй раз – в систему ограничений спроса.
2. Математическая модель транспортной задачи.
Пусть хij – количество груза, перевозимого с i-го в j-й пункт.
Целевая функция: ![]()
Система ограничений:
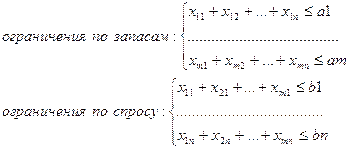
Для решения задачи составляется таблица. В клетки таблицы записывается стоимость соответствующих перевозок сij и в них же заносятся значения перевозок xij, удовлетворяющих поставленным ограничениям. Клетки с не нулевыми перевозками называются базисными, а с нулевыми – свободными. В зависимости от соотношения между запасами и заявками транспортная задача называется сбалансированной или несбалансированной.
Сбалансированная ТЗ:![]()
Несбалансированная ТЗ: ![]()
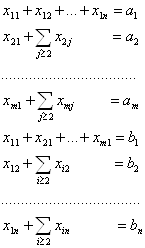
Для сбалансированной ТЗ ограничения принимают вид равенств, то есть получаем m+n ограничений, в которых все переменные линейно зависимы. В результате допустимое решение сбалансированной ТЗ может быть получено, если заполнять клетки транспортной таблицы таким образом, чтобы сумма перевозок в каждой строке ![]() должна быть равна запасам ai, а сумма перевозок в каждом столбце
должна быть равна запасам ai, а сумма перевозок в каждом столбце ![]() равна соответствующей заявке вj. Вариантов заполнения транспортной таблицы множество, поэтому искомым решением является то из допустимых решений, для которых общая стоимость перевозок будет минимальной.
равна соответствующей заявке вj. Вариантов заполнения транспортной таблицы множество, поэтому искомым решением является то из допустимых решений, для которых общая стоимость перевозок будет минимальной.
Похожие работы
... продукции второго вида. В этом случае предприятие получит прибыль денежных единиц. 2. Решить транспортную задачу распределительным методом, оценивая свободные клетки по методу потенциалов. 60 50 85 75 65 8 10 6 5 65 80 4 30 3 50 5 9 35 11 25 4 4 8 10 90 5 5 5 3 85 6 Проверим необходимое ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
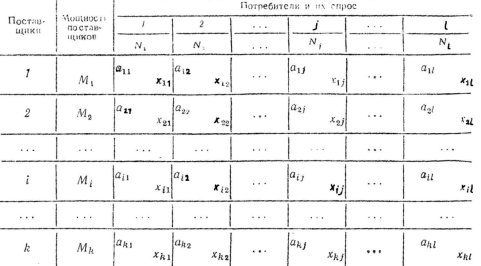
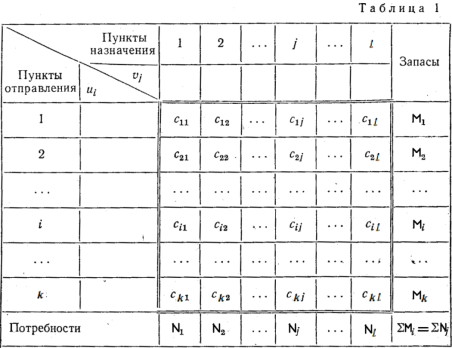
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...





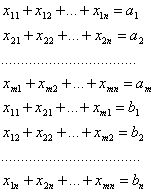


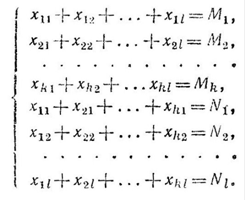

0 комментариев