Навигация
Решение задач линейного программирования транспортной задачей
![]() Федеральное агентство по образованию
Федеральное агентство по образованию
Федеральное государственное образовательное учреждение
среднего профессионального образования
Железногорский горно-металлургический колледж
КУРСОВАЯ РАБОТА
по дисциплине «Математические методы»
(230105.51)
Решение задач линейного программирования транспортной задачей
Выполнил студент гр. ПО-08
А.В. Гудов
Проверил преподаватель:
Н.А. Панасенко
2010 г.
Содержание
Введение
1. Характеристика класса задач
1.1 Общий вид решения и обобщение транспортной задачи
2. Содержательная постановка задачи
3. Математическая постановка задачи
4. Решение задачи
4.1 Математическое решение задачи
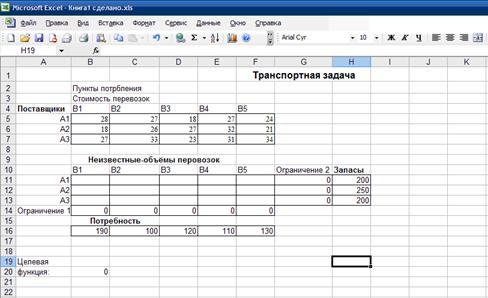
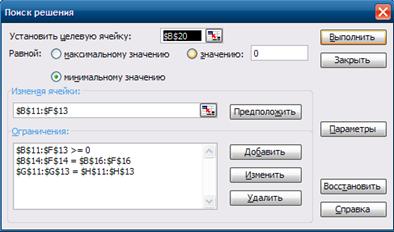
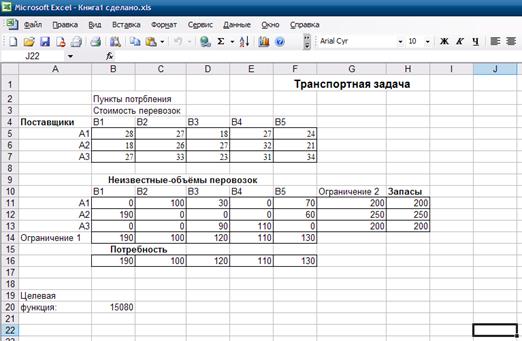
4.2 Решение задачи с помощью программы MS Excel
4.3 Листинг программы
4.4 Руководство пользователя
5. Анализ результатов
Заключение
Список используемой литературы
Введение
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Распределительные задачи связаны с распределением ресурсов по работам, которые необходимо выполнить. Задачи этого класса возникают тогда, когда имеющихся в наличии ресурсов не хватает для выполнения каждой работы наиболее эффективным образом. Поэтому целью решения задачи, является отыскания такого распределения ресурсов по работам, при котором либо минимизируются общие затраты, связанные с выполнением работ, либо максимизируется получаемый в результате общий доход. Основной целью задачи является минимизировать затраты на транспортировку продукции потребителям.1. Характеристика класса задач 1.1 Общий вид решения и обобщение транспортной задачи
Пусть требуется перевезти груз из пункта А1, А2,…,Аnв пункты В1, В2,…,Вn.
а11, а12,…,аnk- стоимость перевозки из пункта Аi в пункт Вj.
А1=100; А2=200; А3=150; В1=80; В2=90; В3=120; В4=160.
Распределить продукцию так со склада, чтобы затраты были минимальные.
Построим начальную таблицу для заполнения ячеек:
Таблица 1
Начальная таблица для заполнения ячеек
| 4 | 7 | 7 | 1 | 100 | |||||
| 80 | 20 | ||||||||
| 12 | 3 | 8 | 8 | 200 | |||||
| 70 | 120 | 10 | |||||||
| 8 | 10 | 16 | 5 | 150 | |||||
| 150 | |||||||||
| 80 | 90 | 120 | 160 | ||||||
Прежде чем начать заполнение ячеек, необходимо проверить условие:
Сумма запаса и сумма потребления были равны:
100+200+150=80+90+120+160; 450=450.
Принцип заполнения ячеек состоит в том, чтобы в выбранную ячейку заносилось минимальное число из стоящих напротив ячеек с параметрами, например: для заполнения ячейки 1-А берутся значения 80 и 100: min= (80;100). Затем меньшее число вычитается из обеих ячеек-значений.
После заполнения необходимо найти целевую функцию:
Z=80*4+20*7+70*3+120*8+10*8+150*5=3180
Получение начального опорного плана
- метод северо-западного угла
- метод наименьшей стоимости
I. Метод наименьшей стоимости:
· Определим ячейку с наименьшей стоимостью;
· Распределим как можно больше единиц в эту ячейку и вычеркнем строку или столбец, который исчерпан;
· Найдем ячейку с наименьшей стоимостью из оставшихся;
· Повторим пункт 2 и 3 пока все единицы не будут распределены.
Таблица 2
Определение ячеек методом наименьшей стоимости.
| 4 | 7 | 7 | 1 | 100 | ||||
| 100 | ||||||||
| 12 | 3 | 8 | 8 | 200 | ||||
| 90 | 110 | |||||||
| 8 | 10 | 16 | 5 | 150 | ||||
| 80 | 10 | 60 | ||||||
| 80 | 90 | 120 | 160 | |||||
Находим целевую функцию:
100*1+90*3+110*8+80*8+10*16+60*5=2350
Получили начальное решение.
II. Проверка решения на оптимальность:
- метод по камням
- метод Modi.
Проверка на оптимальность заключается в оценке пустых ячеек, используя так называемый цикл.
Метод по камням:
Камни – заполненные ячейки
· Поставим знак «+», в ячейку которую оцениваем;
· Двигаясь горизонтально или вертикально к заполненной ячейке(при этом можем пропустить заполненную или пустую ячейку которая, разрешит следующий переход к заполненной ячейке), поставим знак «-»;
· Изменяем направление и перемещаемся к другой заполненной ячейке, выбираем ту разрешит следующий переход, ставим в нее знак «+»;
· Процесс перемещения в заполненной ячейке и чередование знаков продолжаем пока не вернемся к первоначальной.
Таблица 3
Оценивание ячеек
| 1-А | |
| 1А+4 | -8 3А |
| 3D+5 | -1 1D |
| 0 | |
| 1-C | |
| 1C+7 | -1 1D |
| 3D+5 | -16 3C |
| -5 | |
Оценка пустых ячеек методами возможна при условии: число заполненных ячеек равна сумме строк и столбцов и -1:
k=R+L-1
Значение оценки показывает на сколько сократятся(увеличатся) затраты на перевозку единиц продукции если в эту ячейку переместить значение.
Выбираем из оценок наибольшее по модулю отрицательное значение. Из отрицательных выбираем наименьшее и вычитаем его из всех ячеек пути.
Таблица 4
Изменение начальной таблицы
| 4 | 7 | 7 | 1 | 100 | |||||
| 10 | 90 | ||||||||
| 12 | 3 | 8 | 8 | 200 | |||||
| 90 | 110 | ||||||||
| 8 | 10 | 16 | 5 | 150 | |||||
| 80 | 70 | ||||||||
| 80 | 90 | 120 | 160 | ||||||
Таким образом, производим решение, находя новое оптимальное решение пока все оценки пустых ячеек будут содержать только положительные значения и нули.
Метод MODI (модифицированное распределение).
Оценка пустых ячеек вычислением индексных значений строки и столбца.
Этот метод состоит из шагов:
1) Сделать начальное распределение (интуитивный подход), проверить матрицу на полноценность, в случае необходимости провести корректировку.
2) Получить номер индекса для каждой строки и столбца. Делая это используя только заполненные ячейки. Всегда есть по крайней мере одна заполненная ячейка в каждом столбце и строке.
а) начинаем, назначая ноль в первой строке
б) определить индекс столбца для любой заполненной ячейки в строке 1, используя следующие соотношения:
индекс столбца = U;
индекс строки = V;
затраты ячейки = С;
U = C-V
в) Каждое новое значение столбца позволит вычислить по крайней мере 1 новое значение строки и наоборот. Продолжайте эту процедуру пока все строки и столбцы будут заполнены индексами.
3) Получить оценки для пустых ячеек
W – оценка ячейки
W = C- (U+V)
1 – C: W = 7-(0+9) = -2
2 – A: W = 4-(1+3)= 0
4) Получение наилучшего решения
Наличие отрицательных ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение.
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... получение которого связано с большим объемом вычислительных работ. Обычно рассмотренный метод используется при вычислениях с помощью ЭВМ. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической ...
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...

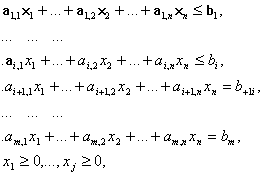
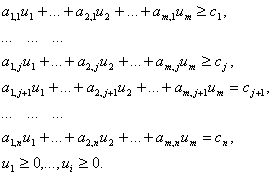







0 комментариев