Навигация
Особенности вычисления определителя матрицы
Содержание
Введение........................................................................................................... 2
1. Постановка задачи...................................................................................... 3
2. Математические и алгоритмические основы решения задачи.................. 5
2.1 Определитель матрицы............................................................................. 5
2.2 Метод Гаусса для решения систем линейных уравнений........................ 6
2.3 Метод Гаусса для вычисления определителя........................................... 8
3. Функциональные модели и блок-схемы решения задачи.......................... 9
4. Программная реализация решения задачи.............................................. 11
5. Пример выполнения программы.............................................................. 16
Заключение.................................................................................................... 18
Список использованных источников и литературы.................................... 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
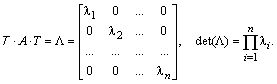
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
Пример 1.
Вычислить определитель матрицы методом A исключения Гаусса.
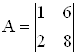 .
.
Решение:
Приведем матрицу к диагональному виду методом Гаусса.
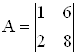 ~
~![]() .
.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
![]() .
.
Знак определяется количеством обменов строк, следовательно определитель матрицы ![]() .
.
Пример 2.
Вычислить определитель матрицы методом A исключения Гаусса.
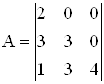 .
.
Решение:
Приведем матрицу к диагональному виду методом Гаусса.
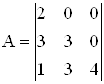 ~
~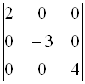 .
.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
![]() .
.
Знак определяется количеством обменов строк, следовательно определитель матрицы ![]() .
.
2. Математические и алгоритмические основы решения задачи
2.1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать ![]() или det A.
или det A.
Определение. Определителем квадратной матрицы
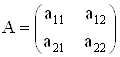
второго порядка называется число
![]() .
.
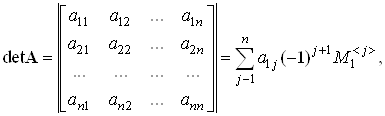
Определителем
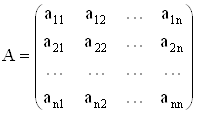
квадратной матрицы порядка n, ![]() , называется число
, называется число
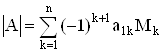
где ![]() - определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
- определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
Похожие работы
... так и ВּА, существует, так как матрицы согласованны: ·==·==; ·==·== = = АּВ=ВּА, т. е. данные матрицы коммутирующие. ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ План 1. Определители квадратной матрицы и их свойства. 2. Теоремы Лапласа и аннулирования. Ключевые понятия Алгебраическое дополнение элемента определителя. Минор элемента определителя. ...
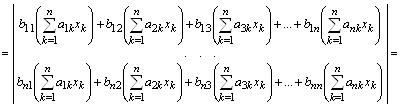
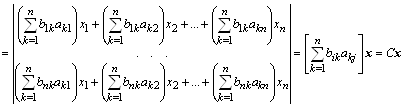
... его за прямые скобки. Оставшиеся коэффициенты упорядочены, как в матрице . Теперь для представления исходной системы уравнений в виде несложно определить векторно-матричную операцию , результатом которой является вектор с i-той компонентой, равной . Аксиоматическое построение линейной (векторной) алгебры с рассмотренными базовыми операциями позволило установить важные и полезные свойства, как ...
... – матрица проводимостей, обратная матрице сопротивлений ветвей. Если в функции fk и jk входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk и jk процессы в этой линейной или нелинейной электрической цепи ...
... и методом Крамера на примере следующей системы В этом случае матрица коэффициентов А и вектор свободных членов b имеют вид Введём матрицу A и вектор b в рабочий лист MS Excel (см. рис. 21) Рисунок 21 В нашем случае матрица А находится в ячейках B1:Е4, а вектор b -G1:G4. Сначала решать систему будем методом обратной матрицы. Поэтому необходимо вычислить матрицу, обратную A. Для ...
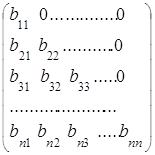
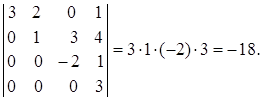
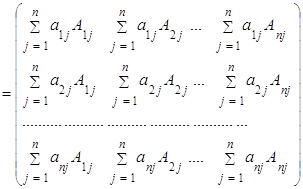
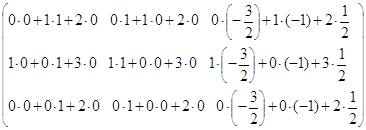
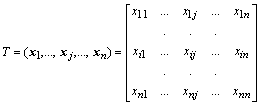
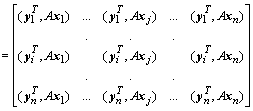

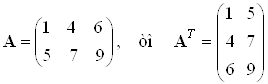

0 комментариев