Навигация
Поняття граф-схеми алгоритму та правила її складання
1.2 Поняття граф-схеми алгоритму та правила її складання
Граф-схема алгоритму (ГСА) є найбільш наочною формою подання роботи автомата. ГСА – це орієнтоватий зв’язний граф, що містить вершини чотирьох типів (рис. 1). Кожен з існуючих входів і виходів вершин може розгалужуватись потрібну кількість разів.
 | |||||||
 |  | ||||||
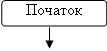 | |||||||
![]()
Вершина "Початок" входів не має. Вершина "Початок" (рис. 1а) і будь-яка операторна (рис. 1г) вершина мають по одному виходу. Вершина "Кінець" (рис. 1б) виходів не має. Будь-яка умовна вершина (рис. 1в) має два виходи, які позначаються символами "Так" і "Ні". Замість цих символів можуть бути використані цифри "1" і "0" відповідно.
ГСА повинна задовольняти таким вимогам:
1) містити скінченне число вершин;
2) мати лише одну початкову та одну кінцеву вершини;
3) входи і виходи кожної з вершин повинні з‘єднуватися дугами, спрямованими від виходу попередньої до входу наступної вершини;
4) кожний вихід повинени з’єднуватись тільки з одним входом;
5) будь-який вхід повинен з’єднуватись принаймні з одним виходом;
6) для будь-якої вершини графа існує хоча б один шлях до кінцевої вершини;
7) у кожній умовній вершині записуєтья тільки один з елементів множини логічних умов;
8) у кожній операторній вершині записується один або деклька операторів, які можуть одночасно виконуватись, при чому допускається, що операторна вершина буде пустою.
1.3 Основні поняття теорії цифрових автоматів
Необхідність формального опису роботи комп’ютера та його окремих частин в процесі проектування вимагає використання спеціального математичного апарату, який необхідний при будь-яких розробках різних методів обробки інформації, при синтезі і аналізі інформаційних процесів, які відбуваються при роботі пристрою. Для цього вводять поняття абстрактного цифрового автомата.
Цифровим автоматом (ЦА) називають пристрій, призначений для обробки та перетворення цифрової інформації. Найбільш розповсюдженим типом цифрових автоматів є комп’ютери.
Цифровим автоматом вважаються пристрої, які характеризуються набором деяких внутрішніх станів ![]() , в які потрапляє автомат під впливом вхідних сигналів і відповідних команд розв’язання задачі ( Рис. 2 ).
, в які потрапляє автомат під впливом вхідних сигналів і відповідних команд розв’язання задачі ( Рис. 2 ).
|
Рис. 2 – Цифровий автомат
Відповідно до Рис. 2, математичною моделлю ЦА є деякий абстрактний автомат, який задається таким чином, в початковий момент часу t = t0, внутрішній стан автомата а(t0) = a1 і зберігається таким до моменту часу t = t1, коли змінюється на стан а2, ця зміна відбувається під впливом вхідного сигналу Х(t1). При цьому формується вихідний сигнал Y(t1)=Y1, який визначається як функція від внутрішнього стану a1 і вхідного сигналу х1: Y=λ(a1, х1). В загальному випадку вважається, що при поданні довільного сигналу хі автомат переходить від стану а(t) в стан а(t+1), який, в свою чергу, є функцією від попереднього стану і вихідного сигналу. В результаті цього переходу виробляється відповідний сигнал Y.
Абстрактний ЦА описується шістьма основними параметрами:
- а1 – початковий стан автомата;
- А = {![]() } - множина (алфавіт) внутрішніх станів;
} - множина (алфавіт) внутрішніх станів;
- Х = {![]() } - алфавіт вхідних сигналів;
} - алфавіт вхідних сигналів;
- Y = {![]() } – алфавіт вихідних сигналів;
} – алфавіт вихідних сигналів;
- δ = {![]() } – сукупність функцій переходу автомата з одного стану в інший;
} – сукупність функцій переходу автомата з одного стану в інший;
- λ = {![]() } – сукупність функцій виходу автомата.
} – сукупність функцій виходу автомата.
Сукупність правил переходу автомата з одного стану в інший залежно від вхідної інформації і внутрішніх станів називається алгоритмом перетворення інформації в цифровому автоматі.
На відміну від абстрактного автомата, реально використовуються кінцеві автомати, які мають кінцеві множини вхідних сигналів, вихідних сигналів та внутрішніх станів. Всі кінцеві автомати поділяються на цілком визначені, у яких область визначення D функцій δ та λ збігається з множиною перетину алфавітів вхідного та станів, яка є в свою чергу множиною пар ![]() ; та нецілком визначені часткові кінцеві автомати, для яких функції внутрішніх станів і вихідних сигналів δ та λ визначаються не для всіх пар
; та нецілком визначені часткові кінцеві автомати, для яких функції внутрішніх станів і вихідних сигналів δ та λ визначаються не для всіх пар ![]() , Крім того кінцеві автомати підрозділяють за виглядом функцій виходів
, Крім того кінцеві автомати підрозділяють за виглядом функцій виходів ![]() та переходів
та переходів ![]() . За цією ознакою автомати поділяються на автомати Мілі та Мура.
. За цією ознакою автомати поділяються на автомати Мілі та Мура.
Будь-який автомат можна описати функцією стану і вихідною функцією:
![]() (3)
(3)
Цьому виразу відповідає автомат, який називається автоматом Мілі. На відміну від нього, для автомата Мура функція стану не змінюється, а вихідний сигнал залежить тільки від внутрішнього стану автоматів:
![]() (4)
(4)
1.4 Синтез керуючого автомата
Процес синтезу керуючого автомату включає такі етапи:
1. Кодоване представелення графа мікропрограми або отримання граф-схеми алгоритма роботи керуючого автомата.
2. Розмічування граф-схеми алгоритму для визначення станів керуючого автомата, який функціонує відповідно до вибранї моделі (Мілі або Мура).
3. Складання структурної таблиці переходів та виходів автомата.
4. Отримання функцій збудження елементів пам’яті (тригерів).
5. Побудова комбінаційної частини автомата.
Кодоване представлення граф-схеми алгоритму здійснюється шляхом заміни мікрокоманд, записаних в операторних вершинах, відповідними їм керуючими сигналами yj , а умов, які перевіряються в умовних вершинах, відповідними їм сигналами Xi.
Для автомата Мура вихідний сигнал залежить лише від внутрішнього стану, тобто y=λ(a). Тому кожна операторна вершина повинна бути відмічена символом вихідного стану автомата аі.
Для побудови автомата Мілі слід пам’ятати, що вихідний сигнал залежить як від внутрішнього стану, так і від вхідного сигналу (тобто умови Хі). Кодування граф-схеми автома Мілі відбувається не так, як для автомата Мура. Символом а0 кодується вхід першої вершини графа, що йде за початковою, і вхід кінцевої вершини. Виходи інших операторних вершин відмічаються символами аі, при чому виходи різних вершин мають різні номери станів.
За кодованою граф-схемою роботи автомата складається таблиця переходів і виходів. Для цього спочатку здійснюють кодування станів автомата двійковими кодами, визначають тип та кількість тригерів. Потім за таблицею преходів визначають значення сигналів на входах тригерів, при яких здійснюються переходи; визначають функції збудження тригерів та виконують їх мінімізацію. За знайденими виразами будується комбінаційна схема керуючого автомата на обраних елементах.
Таблиця переходів і виходів має однаковий вигляд для автоматів Мілі та Мура і будується в наступній послідовності.
В полі аi графи t таблиці 2 записуємо поточний стан автомата, в полі аі графи t+1– наступний його стан, у полі Х –умову переходу зі стану аi(t) в стан аi(t+1) згідно граф-схеми алгоритму. В полі Y записуються мікрооперації, які виконуються при переході автомата в наступний стан. У полі “Тригери” вказано сигнали, які необхідно подати на входи відповідних запам’ятовуючих елементів. Таким чином описуються всі можливі переходи автомата (табл. 2).
Таблиця 2– Таблиця переходів і виходів автомата
| t | t+1 | Тригери | |||||
| ai | Xі | ai | yi | Т1 | Т2 | … | Тn |
Кількість тригерів, які необхідні для організації пам’яті керуючого автомату, визначається як найближче більше ціле від двійкового логарифму кількості станів за формулою (5):
R = ] log2 M [ , (5)
де М – кількість станів автомата,
R – шукана кількість тригерів.
За отриманою таким чином таблицею записуються та зводяться до мінімальної форми функції збудження тригерів та функції виходів цифрового автомата. Слід пам’ятати, що функції виходів цифрового автомата Мура залежать лише від внутрішніх станів (графа ai поля t+1) і не залежать від умов переходу Хі.
Далі обирається система елементів, з яких будується схема автомата. У більшості схем як елементи пам’яті використовуються елементарні автомати (тригери), що мають наступні особливості:
1) вони є автоматами Мура і мають два стійких стани;
2) станам елементарного автомата відповідають два різних вихідних сигнали: одиничний (коли на прямому виході тригера одиниця, а на інверсному – нуль) та нульовий;
3) у загальному випадку елементарний автомат може мати декілька фізичний входів;
Крім того, схема будь-якого керуючого автомата повинна містити певну кількість логічний елементів, що утворюють функціонально повну систему для синтезу необхідної комбінаційної схеми.
Похожие работы
... на відповідну кількість одиниць. Показова форма подання чисел має і свої вади, основною з яких є порівняно висока складність виконання арифметичних операцій, а отже, і більша вимогливість до ресурсів обчислювального пристрою. Це обмежує її застосування, наприклад, у спеціалізованих радіотехнічних обчислювальних пристроях, у системах управління технологічними процесами та обробки вимірювальної і ...
... в одному розряді перетворюється в 1, а в другому розряді 1 в 0). 2.4 Управляючий автомат(Каган стр.241 - 243) Будь-який цифровий пристрій складається з двох частин – операційного та управляючого блоків. Операційний блок характеризується сукупністю визначених в ньому мікрооперацій, кожна з яких являє собою деякий виконуваний в даному операційному блоці елементарний акт передачі або перетворення і ...
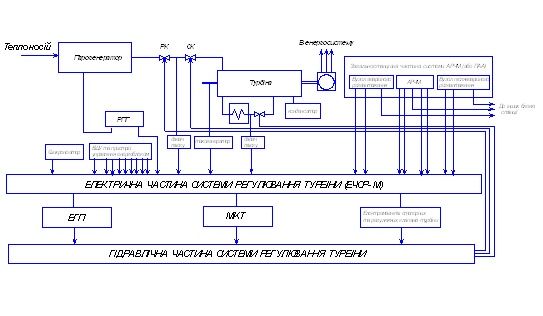
... , звитих в плоскі спіралі. Кінці спіралей приварені до трьох роздаючих і до трьох колекторних труб. 2. Призначення, склад, технічні характеристики системи автоматичного регулювання 2.1 Призначення системи автоматичного регулювання Система автоматичного регулювання (САР) турбіни виконується електрогідравлічною і структурно складається з електричної і гідравлічної частин, робота яких взає ...
... вам найбільше? - То чи сподобався вам сьогоднішній урок і чим? Вже дзвінок нам дав сигнал, Для перерви час настав, Тож не буду вас тримати, Біжіть швидше відпочивати. VI. Домашнє завдання. Урок № 2 Тема. Обчислювальні прилади. Мета. Донести до дітей інформацію, як появились перші обчислювальні прилади, зокрема машина «Паскаліна», хто її створив; навчити грати гру лабіринт, а також ...

0 комментариев