Контроль виконання арифметичних операцій

1.5 Контроль виконання арифметичних операцій

Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Припустимо, що зображення чисел зберігаються в машині в деякому коді, тобто операція перетворення в заданий код або обернений проводиться на виході чи вході машини. Методика реалізації операцій контролю представляється таким чином.

По-перше, розглянемо зображення числа у відповідному коді як єдину кодову комбінацію.

Розглянемо послідовність дій на прикладі суматора прямого коду: якщо додаються тільки цифрові частини зображення чисел, а знак зберігається, то контроль можна здійснити двома способами:

1)   розділений контроль знакової і цифрової чистин зображень результату;

2)   загальний контроль всього зображення .

При розділеному способі для контролю знакових розрядів можна використовувати засіб для визначення переповнення, оскільки у випадку модифікованого коду поява помилок в знакових розрядах призведе до неспівпадання інформації в них. При перевірці правильності обробки цифрових частин зображень також не виникає особливих труднощів .

При загальному способі контролю необхідна корекція контрольного коду результату через те, що знак результату при додаванні повторює знак доданків. Загальний спосіб контролю може бути використаний і для суматорів оберненого і доповняльного кодів. При додаванні чисел на суматорі доповняльного коду можлива корекція контрольного коду в випадку, якщо знакові розряди зображень містять одиницю тому, що при цьому виникає одиниця переносу із знакового розряду. Очевидно, що контрольний код суми буде рівним

,

де – кореляція (=1, якщо виник перенос із знакового розряду, і =0 – якщо переносу немає).

Контроль по модулю. Різноманітні задачі можна вирішувати за допомогою метода контролю, заснованого на властивостях порівняння. Розвинені на цій основі методи контролю арифметичних і логічних операцій називають контролем по модулю.

Існують два метода отримання контрольного коду: числовий і цифровий.

Числовий метод контролю. При числовому методі контролю код заданого числа знаходиться як найменший додатній залишок від ділення числа на обраний модуль р:

, (6)

де  – модуль числа,

{А/р} – ціла частина від ділення числа,

А – контрольне число.

Величина модуля р значно впливає на якість контроля; якщо p = q(де q – основа системи числення, в якій виражене число) і має місце числовий контроль, то контролюється тільки молодший розряд числа і контроль не має сенсу; для  справедливі аналогічні роздуми, тому, що якщо (де n розрядність числа), знову не всі розряди числа беруть участь в контролі і помилки в розрядах які старші m взагалі не сприймаються.

При числовому методі контролю по модулю р для знаходження залишку використовують операцію ділення, яка потребує значних витрат машинного часу.

Цифровий метод контролю. При цифровому методі контролю контрольний код числа утворюється діленням суми цифр числа на обраний модуль:

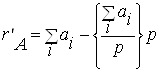
або , (7)

 

де  – модуль числа,

 – -та цифра числа.

Можливі два шляхи отримання контрольного коду:

1)    безпосереднє ділення суми цифр на модуль р;

2)    сумування цифр за модулем р.

Другий шлях простіше реалізується, оскільки якщо a_i<p, то контрольний код отримується лише операцією сумування.

Проте при цифровому методі властивості порівнянь не завжди справедливі. Це відбувається через наявність переносів (запозичень) при наявності арифметичний дій над числами. Тому знаходження контрольного коду результату операції відбувається обов’язково з корекцією.

Арифметичний контроль (AN-контроль) вимагає утворення контрольного коду у вигляді AN, де А – контрольоване число, N – модуль. Вагою арифметичного коду прийнято вважати кількість ненульових символів у кодовій комбінації, а відстань, що визначається як вага різниці кодових комбінацій, називається арифметичною відстанню.

Якщо відстано між двома числами А₁ та А₂ рівна d, то це означає, що перехід від одного числа до другого досягається додаванням величини d. У цьому випадку всі комбінації чисел, що знаходяться між А₁ та А₂, є забороненими. Відповідно, для виявлення d-кратної помилки необхідно мати відстань не меншу за d+1. Якщо d=1, то такий код не зможе виявляти помилки. Величина відстані для кодів AN-вигляду залежить від величин А та N.

Для будь-якого числа А в системі основи q=2 існує єдине представлення вигляду  де а_і=±1 або 0, в якому немоє двох сусідніх коефіцієнтів, відмінних від нуля.

Таке представлення містить мінімальне число ненульових коефіцієнтів і називається канонічним. У канонічному представленні вага будь-якого числа, починаючи з 2^і+1 й до числа 2^і+2^і-1, на одиницю більша за вагу чисел від 1 до 2^і-1. Вага чисел, починаючи з 2^і+2^і-1+1 і до 2^і+1, співпадає з вагою чисел 2^і+2^і-1-1, 2^і+2^і-1-2 і т.д.

Кількість розрядів для представлення числа AN дорівнює log₂(AN)=log₂A+log₂N, де log₂N – надлишковість кода. Таким чином, вибір модуля визначає не тільки надлишковість, але й відстань. В якості модуля доцільно вибирати деяке взаємно просте з основою системи q число, що перевищує саму основу. Можна припустити, що для двійкової системи N=3, і тоді будь-який код вигляду А·3 буде виявляти всі поодинокі помилки. Відповідно, мінімальна надлишковість при довільній основі визначається як log_q(q+1), тобто завжди потрібно буде не менше одного, але й не більше двох додаткових розрядів.

Коди з мінімальною відстанню більшою за 2, характеризуються величиною M_q(N, d). Величина M_q(N, d) – найменше число, яке при множенні його на N дає число, вага якого менша за d у представленні за основою q. Іншими словами, якщо число N мало вагу d у представленні за основою q, то добуток N·M_q(N, d) матиме вагу, меншу від d за цією самою основою q.

Якщо число А змінюється в межах 0 ≤А ≤ M_q(N, d) , то при будь-яких N і q мінімальна відстань А·N-кода буде дорівнювати щонайменш d, що випливає з певної кількості M_q(N, d).

В теорії кодування доведено, що M₂(N, 3)=(2^(N-1)/2+1)/N.

Основний спосіб для відшукання значення М_q – спосіб безпосередніх обчислень (див. Савєльєв А.Я., ст. 163).