Навигация
Нахождение приближенных (грубых) значений корней
19131
знак
0
таблиц
6
изображений
2. Нахождение приближенных (грубых) значений корней.
3. Вычисление корней с требуемой точностью.
Первая и вторая задача решаются аналитическими и графическими методами.
Отделение корней
Если уравнение f(x) = 0 имеет только действительные корни, то полезно составить таблицу значений функции f(x).Если в двух соседних точках 
и 
функция имеет разные знаки, то между этими точками лежит по меньшей мере один корень. Корень будет заведомо единственным, если 
определена на отрезке [,] и сохраняет постоянный знак.
Графические методы
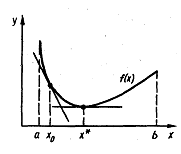
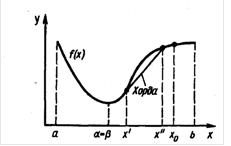
Действительные корни уравнения f(x) = 0 приближенно можно определить как абсциссы точек пересечения графика функции f(x) с осью x.
Приближенные значения корней, найденные грубо, в дальнейшем уточняют с помощью какого-либо итерационного метода.
Метод дихотомии
Дихотомия означает деление пополам. Пусть нашли такие точки 
и 
, что 
< 0, т.е. на [,] лежит по меньшей мере один корень. Найдем середину отрезка [,]. Получаем 
. Если f(x2) = 0, то 
если f(
)
0, то из двух половин отрезка выберем ту, для которой выполняется условие 
< 0, т.к. корень лежит на этой половине. Затем вновь делим выбранный отрезок пополам и выбираем ту половину, на концах которой функция имеет разные знаки.
Если требуется найти корень с точностью 
, то продолжим деление пополам (если конечно функция в середине какого-либо отрезка не обращается в нуль), пока длина очередного отрезка не станет < 2. Тогда середина последующего отрезка установит значение с требуемой точностью. Метод дихотомии прост и очень надежен. Он сходится для любых непрерывных функций f(x), в том числе не дифференцируемых.
Метод устойчив к ошибкам округления, но скорость сходимости невелика. К недостаткам метода следует отнести сходимость к неизвестно какому корню (если корни не отделены). Но указанный недостаток имеется у всех итерационных методов. Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна. Метод иногда применяется для грубого нахождения корней с последующим уточнением по другому методу с большей скоростью сходимости.
Этот метод относится к двусторонним (или к двух шаговым) методам, т.к. для вычисления очередного приближения необходимо знать два предыдущих.
2.2 Алгоритм решения
Для нахождения максимума функции будем перебирать всевозможные переменные xi, 
, с шагом необходимой длины.
Затем будем находить значение функции с(
) методом дихотомии.
Для этого вычислим производную функции 
, зависящей от с, и приравняем ее к 0.
Найдем корень 
этого нелинейного уравнения методом дихотомии.
Подставим конкретный набор 
и при нем найденное в исходную функцию, и получим ее значение.
Перебирая все xi, найдем максимум функции.
Перебирая всевозможные параметры p и q, получим некоторые наборы 
(в зависимости от p и q) на которых функция достигает максимума.
Похожие работы
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...
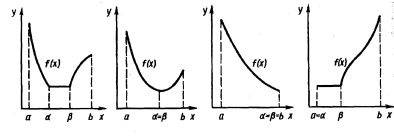
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
0 комментариев