Навигация
Решение задачи с использованием метода покоординатного спуска
3. Решение задачи с использованием метода покоординатного спуска
3.1 Описание метода покоординатного спуска
Изложим этот метод на примере функции трех переменных ![]() .
.
Выберем нулевое приближение ![]() . Фиксируем значения двух координат
. Фиксируем значения двух координат ![]() . Тогда функция будет зависеть только от одной переменной
. Тогда функция будет зависеть только от одной переменной ![]() ; обозначим ее через
; обозначим ее через ![]() . Найдем минимум функции одной переменной
. Найдем минимум функции одной переменной ![]() и обозначим его через
и обозначим его через ![]() . Мы сделали шаг из точки
. Мы сделали шаг из точки ![]() в точку
в точку ![]() по направлению, параллельному оси
по направлению, параллельному оси ![]() ; на этом шаге значение функции уменьшилось.
; на этом шаге значение функции уменьшилось.
Затем из новой точки сделаем спуск по направлению, параллельному оси ![]() , т. е. рассмотрим
, т. е. рассмотрим ![]() , найдем ее минимум и обозначим его через
, найдем ее минимум и обозначим его через ![]() . Второй шаг приводит нас в точку
. Второй шаг приводит нас в точку ![]() . Из этой точки делаем третий шаг – спуск параллельно оси
. Из этой точки делаем третий шаг – спуск параллельно оси ![]() и находим минимум функции
и находим минимум функции ![]() . Приход в точку
. Приход в точку ![]() завершает цикл спусков.
завершает цикл спусков.
Будем повторять циклы. На каждом спуске функция не возрастает, и при этом значения функции ограничены снизу ее значением в минимуме ![]() . Следовательно, итерации сходятся к некоторому пределу
. Следовательно, итерации сходятся к некоторому пределу ![]() . Будет ли здесь иметь место равенство, т. е. сойдутся ли спуски к минимуму и как быстро?
. Будет ли здесь иметь место равенство, т. е. сойдутся ли спуски к минимуму и как быстро?
Это зависит от функции и выбора нулевого приближения.
Метод спуска по координатам несложен и легко программируется на ЭВМ. Но сходится он медленно. Поэтому его используют в качестве первой попытки при нахождении минимума.
3.2 Алгоритм решения
Будем перебирать с с шагом какой-либо малой длины.
Зададим нулевое приближение, например:
![]()
Найдем частные производные ![]() .
.

Пусть при каком-то j ![]()
Тогда k-ое приближение считаем по формулам:
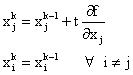
Шаг t будем выбирать таким образом, чтобы
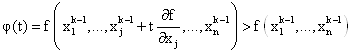 и
и ![]() .
.
В результате, закончив процесс по критерию ![]()
![]()
![]() , где
, где ![]() -заданная точность мы придем к набору
-заданная точность мы придем к набору![]() , при котором функция f максимальна.
, при котором функция f максимальна.
Подставим найденный набор ![]() и соответствующее
и соответствующее ![]() в функцию f1=
в функцию f1=![]() и перебрав все с, выберем те
и перебрав все с, выберем те ![]() , при которых f1 минимальна.
, при которых f1 минимальна.
Заключение
В ходе решения поставленной задачи рассмотрены случаи, когда n=4,5,6. Были найдены две основные области наборов ![]() :
:
1) xi=0 или 1(количество 0 и 1 одинаково)
2) xi=0.5, ![]() .
.
Причем участок 1<p<1.5 покрыт первой областью, при q>>p ![]() –– из первой области, при q≈p
–– из первой области, при q≈p ![]() –– из второй области, а при p→∞ область делилась между ними примерно пополам.
–– из второй области, а при p→∞ область делилась между ними примерно пополам.
На участке p>2 появлялись области вида:
i<k => xi=0;
i>n-k => xi=1;
k-1<i<n-k+1=> xi=0.5.
На участке 2<q<3 p![]() 2 существует область, в которой максимум достигается при
2 существует область, в которой максимум достигается при ![]() вида:
вида:
xi=a => xn-i=1-a, 0<a<1.
Список использованных источников
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 543с.
2. Березин И.С. и Жидков Н. П. Методы вычислений. т.1. М.: “Наука”, 1965. 633c.
3. Подбельский В.В. и Фомин С.С. Программирование на языке Си. М.: “Финансы и статистика”, 2000. 599с.
Приложение 1. Листинг программы №1
//вывод на экран областей максимума функции
#include "stdafx.h"
#include "KE2.h"
#include "math.h"
#include "KE2Doc.h"
#include "KE2View.h"
#ifdef _DEBUG
#define new DEBUG_NEW
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
#endif
IMPLEMENT_DYNCREATE(CKE2View, CView)
BEGIN_MESSAGE_MAP(CKE2View, CView)
//{{AFX_MSG_MAP(CKE2View)
// NOTE - the ClassWizard will add and remove mapping macros here.
// DO NOT EDIT what you see in these blocks of generated code!
//}}AFX_MSG_MAP
// Standard printing commands
ON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)
ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint)
ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview)
END_MESSAGE_MAP()
CKE2View::CKE2View()
{
}
CKE2View::~CKE2View()
{
}
BOOL CKE2View::PreCreateWindow(CREATESTRUCT& cs)
{
return CView::PreCreateWindow(cs);
}
void CKE2View::OnDraw(CDC* pDC)
{
CKE2Doc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
drawPoint(pDC);
// TODO: add draw code for native data here
}
BOOL CKE2View::OnPreparePrinting(CPrintInfo* pInfo)
{
// default preparation
return DoPreparePrinting(pInfo);
}
void CKE2View::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/)
{
// TODO: add extra initialization before printing
}
void CKE2View::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/)
{
// TODO: add cleanup after printing
}
#ifdef _DEBUG
void CKE2View::AssertValid() const
{
CView::AssertValid();
}
void CKE2View::Dump(CDumpContext& dc) const
{
CView::Dump(dc);
}
CKE2Doc* CKE2View::GetDocument() // non-debug version is inline
{
ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CKE2Doc)));
return (CKE2Doc*)m_pDocument;
}
#endif //_DEBUG
int sgn(float a)
{
int sg;
if (a>0) sg=1;
if (a==0) sg=0;
if (a<0) sg=-1;
return(sg);
}
#define n 6
void CKE2View::drawPoint(CDC *pDC)
{
double **c,*f1,*f,*x,*w,*e,max,p=2,q=2,xx,yy;
int i=0,j=0,k,m,a,b,*l,bb=0;
c=new double*[10000];
for(i=0;i<10000;i++)
{
c[i]=new double[3];
memset(c[i],0,sizeof(double)*3);
}
f=new double[10000];
e=new double[10000];
w=new double[10000];
f1=new double[10000];
x=new double[n];
l=new int[10000];
for(xx=0.5;xx<1;xx+=0.01)
for(yy=xx;yy<1);yy+=0.01)
{
p=1./(1.-xx);
q=1./(1.-yy);
memset(w,0,sizeof(double)*10000);
memset(e,0,sizeof(double)*10000);
memset(f1,0,sizeof(double)*10000);
memset(x,0,sizeof(double)*n);
x[n-1]=1;
j=0;
for(i=0;i<10000;i++)
{j=0;
f1[i]=1;c[i][0]=0;c[i][1]=1;c[i][2]=0.5;
while(fabs(f1[i])>0.00000001)
{
f1[i]=0;
for(k=0;k<n;k++)
{ f1[i]+=pow((fabs(x[k]-c[i][2])),(p-1))*sgn(x[k]-c[i][2]);}
if (f1[i]<-0.00000001)
{max=c[i][2];c[i][2]=c[i][2]-(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;}
if (f1[i]>0.00000001)
{max=c[i][2];c[i][2]=c[i][2]+(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;}
if (fabs(f1[i])<=0.00000001)
{c[i][0]=c[i][2];goto B;}
}
B:
c[i][0]=c[i][2];
for(a=0;a<n;a++)
{
for(b=0;b<n;b++)
w[i]+=pow((fabs(x[a]-x[b])),q);
e[i]+=pow((fabs(x[a]-c[i][0])),p);
}
f[i]=pow((e[i]/n),(1./p))/pow((w[i]/(n*n)),(1./q));
x[n-2]+=0.1;
for(k=2;k<n;k++)
{
if(x[n-k]>1.04)
{
x[n-k-1]+=0.1;
x[n-k]=x[n-k-1];
for(m=2;m<k;m++)
x[n-m]=x[n-k-1];
}
if (x[0]!=0) goto A;
}
}
A:
max=f[0];k=0;
for(m=0;m<i;m++)
{
if (fabs(max-f[m])<0.001) {k++;l[k]=m;}
if (max<f[m]) {k=0;max=f[m];l[k]=m;}
}
for(a=0;a<n-1;a++)
x[a]=0;
for(a=0;a<l[0];a++)
{
x[n-2]+=0.1;
for(k=2;k<n;k++)
if(x[n-k]>1.04)
{
x[n-k-1]+=0.1;
x[n-k]=x[n-k-1];
for(m=2;m<k;m++)
x[n-m]=x[n-k-1];
}
}
b=0;
for(k=0;k<n;k++)
{
if((x[k]==0)||(fabs(x[k]-1)<0.04)) b++;
else
{
if(fabs(x[k]-0.5)<0.04) b+=2;
else b=-n;
}
}
b-=n;
if (b<0) b=24;
if (b==0) b=58;
if(b==bb) continue;
bb=b;
c=%f\n",p,q,l[0],l[k],k+1,max,c[l[0]][0]);
COLORREF cr(RGB((b%3)*127,(b%4)*85,(b%5)*63));
CBrush r(cr);
CPen rp(PS_SOLID,0,cr);
pDC->SelectObject(&rp);
pDC->SelectObject(&r);
CPoint r1[3]={CPoint(0,360),CPoint(int(720./p),-int(720./q)+360),CPoint(int(720./p),360)};
pDC->Polygon(r1,3);
}
}
Приложение 2. Листинг программы №2.
//Покоординатный спуск
#include<stdAfx.h>
#include<stdio.h>
#include<iostream.h>
#include<conio.h>
#include<math.h>
#define n 4
void main()
{
//double ff(double v,double vv);
int sgn(float a);
double *aa,**x,*f1,f,e,w,w1,e1,q=7,p=7,*r,*z,f2,*r1,max,m=0,c,f20,f21;
int bb,i,MAX,k,j,a,b,mm,ss;
x=new double*[n];
for(i=0;i<n;i++)
x[i]=new double[2];
z=new double[3];
aa=new double[n-2];
r=new double[n];
r1=new double[n];
//f2=new double[n];
f1=new double[n];
for(i=1;i<n-1;i++) //начальное прибл - все х от 1-го до n-2-го равны
x[i][0]=0.1; //
x[n-1][0]=1;x[n-1][1]=1;x[0][1]=0;x[0][0]=0;x[1][0]=0.9;//x[2][0]=0;//x[3][0]=0;x[4][0]=1;//начальное приближение
for(c=0.5;c<0.7;c+=0.1) //Цикл по c
{
bb=0;
for(k=1;;k++) //Цикл по k
{
// for(i=0;i<n;i++)
// cerr<<"x["<<i<<"]="<<x[i][0]<<"\n";
// cerr<<"\n";
w=0;e=0;w1=0;e1=0;
for(a=0;a<n;a++)
r[a]=0;
for(a=0;a<n;a++)
{
for(b=0;b<n;b++)
{
w+=pow((fabs(x[a][0]-x[b][0])),q);
r[a]+=pow((fabs(x[a][0]-x[b][0])),q-1)*sgn(x[a][0]-x[b][0]);
}
e+=pow((fabs(x[a][0]-c)),p);
}
w=pow(w/(n*n),1./q);//знаменатель исх ф-ции
e=pow(e/n,1./p);//числитель исх ф-ции
f=e/w;
//cerr<<"\n"<<f<<"\n";
f1[0]=0;f1[n-1]=0;
MAX=0;
for(j=1;j<n-1;j++)
{
f1[j]=pow(n,(2./q-1./p))*(pow(e,(1./p-1))*pow(fabs(x[j][0]-c),(p-1))*w
*sgn(x[j][0]-c)-2.*pow(w,(1./q-1))*r[j])/(w*w); //производная исх. функции по x[j][0] в точке с координатами x[i][0] i=0..n-1 на k-ом приближении
// cerr<<f1[j]<<"\n";
for(a=0;a<bb;a++)
if(aa[a]==j) break;
if(a!=bb) continue;
if (fabs(f1[j])>fabs(f1[MAX])) MAX=j;
}
// т.к. x[0]=0 и x[n-1]=1 - cosnt
mm=0;ss=0;
for(i=0;;i++)
{
if (mm==0) z[0]=100000000./pow(1.2,i);//шаг
if(mm==1)
{
z[0]=-1000000000./pow(1.2,ss);
ss++;
}
/*if(z[0]<0.000000000000001)
{
z[0]=-0.5/pow(1.5,mm);
mm++;
}*/
for(a=0;a<n;a++)
r1[a]=0;
w1=0;e1=0;
for(a=0;a<n;a++)
{
if(a==MAX)
{
for(b=0;b<n;b++)
{
w1+=pow(fabs(x[a][0]+f1[a]*z[0]-(x[b][0]+f1[b]*z[0])),q);
r1[a]+=pow( fabs(x[a][0]+f1[a]*z[0] - (x[b][0]+f1[b]*z[0]) ),q-1)*
sgn( x[a][0]+f1[a]*z[0] - (f1[b]*z[0]+x[b][0]) );
}
e1+=pow((fabs(x[a][0]+f1[a]*z[0]-c)),p);
}
else
{
for(b=0;b<n;b++)
{
w1+=pow((fabs(x[a][0]-x[b][0])),q);
r1[a]+=pow((fabs(x[a][0]-x[b][0])),q-1)*sgn(x[a][0]-x[b][0]);
}
e1+=pow((fabs(x[a][0]-c)),p);
}
}
w1=pow(w1/(n*n),1/q);e1=pow(e1/n,1/p);
//printf("\n f=%f f[a]=%f",e/w,e1/w1);
a=0;
//for(j=1;j<n-1;j++)
//if (((x[j][0]+z[0]*f1[j])<1)&&((x[j][0]+z[0]*f1[j])>0)) a++;
//if(a<n-2) continue;
if (((x[MAX][0]+z[0]*f1[MAX])<1)&&((x[MAX][0]+z[0]*f1[MAX])>0)) a++;
if(a!=1) continue;
if (e1/w1>e/w) break;
if ((e1/w1-e/w)>-0.00000001)
{
if(z[0]>0)
{
mm=1;
continue;
}
for(a=1;a<n-1;a++)
x[a][1]=x[a][0];
goto A;
}
}
for(j=1;j<n-1;j++)
if(j==MAX) x[j][1]=x[j][0]+z[0]*f1[j];
else x[j][1]=x[j][0];
if(fabs(x[MAX][1]-x[MAX][0])<0.00000001)
{
aa[bb]=MAX;
bb++;
}
if(bb==n-2) break;
for(j=1;j<n-1;j++)
x[j][0]=x[j][1];
} //закрытие цикла по k
A:
cerr<<"K-vo iteratsiy: "<<k-1<<"\n\n";
for(i=0;i<n;i++)
cerr<<"x["<<i<<"]="<<x[i][0]<<"\n";
cerr<<"\nf="<<f<<"\n";
}// закрытие цикла по с
}
int sgn(float a)
{
int sg;
if (a>0) sg=1;
if (a==0) sg=0;
if (a<0) sg=-1;
return(sg);
}
Приложение 3. Листинг программы №3
#include <stdAfx.h>
#include <stdlib.h>
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <iostream.h>
#define n 4
int sgn(float);
main()
{
double **c,*f1,*f,*x,*w,*e,max,p=2,q=2,xx,yy;
int i=0,j=0,k,m,a,b,*l;
c=new double*[10000];
for(i=0;i<10000;i++)
c[i]=new double[4];
f=new double[10000];
e=new double[10000];
w=new double[10000];
f1=new double[10000];
x=new double[n];
l=new int[10000];
for(xx=0.5;xx<1;xx+=0.01)
for(yy=xx;yy<1;yy+=0.01)
{
p=1./(1.-xx);
q=1./(1.-yy);
for(i=0;i<10000;i++)
{
w[i]=0;
e[i]=0;
f1[i]=0;
}
for(i=0;i<10000;i++)
for(j=0;j<3;j++)
{c[i][j]=0;
}
for(i=0;i<n;i++)
x[i]=0;
x[n-1]=1;
j=0;
for(i=0;i<10000;i++)
{j=0;
f1[i]=1;c[i][0]=0;c[i][1]=1;c[i][2]=0.5;
while(fabs(f1[i])>0.000000001)
{
f1[i]=0;
for(k=0;k<n;k++)
{ f1[i]+=pow((fabs(x[k]-c[i][2])),(p-1))*sgn(x[k]-c[i][2]);}
if (f1[i]<-0.000000001)
{max=c[i][2];c[i][2]=c[i][2]-(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;}
if (f1[i]>0.000000001)
{max=c[i][2];c[i][2]=c[i][2]+(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;}
if (fabs(f1[i])<=0.000000001)
{c[i][0]=c[i][2];goto B;}
}
B:
c[i][0]=c[i][2];
for(a=0;a<n;a++)
{
for(b=0;b<n;b++)
w[i]+=pow((fabs(x[a]-x[b])),q);
e[i]+=pow((fabs(x[a]-c[i][0])),p);
}
f[i]=pow((e[i]/n),(1./p))/pow((w[i]/(n*n)),(1./q));
x[n-2]+=0.1;
for(k=2;k<n;k++)
{
if(x[n-k]>1.04)
{
x[n-k-1]+=0.1;
x[n-k]=x[n-k-1];
for(m=2;m<k;m++)
x[n-m]=x[n-k-1];
}
if (x[0]!=0) goto A;
}
}
A:
max=f[0];k=0;
for(m=0;m<i;m++)
{
if (fabs(max-f[m])<0.0001) {k++;l[k]=m;}
if (max<f[m]) {k=0;max=f[m];l[k]=m;}
}
printf("p=%f q=%f max=%f\n",p,q,max);
x[n-1]=1;
for(a=0;a<=n-2;a++)
x[a]=0;
for(a=0;a<l[0];a++)
{
x[n-2]+=0.1;
for(k=2;k<n;k++)
{
if(x[n-k]>1.04)
{
x[n-k-1]+=0.1;
x[n-k]=x[n-k-1];
for(m=2;m<k;m++)
x[n-m]=x[n-k-1];
}
}
}
for(a=0;a<n;a++)
printf("Nabor:x[%d]=%f ",a,x[a]);
}
getch();
return 0;
}
int sgn(float a)
{
int sg;
if (a>0) sg=1;
if (a==0) sg=0;
if (a<0) sg=-1;
return(sg);
}
Приложение №4 Результаты работы программы №1:
n=6
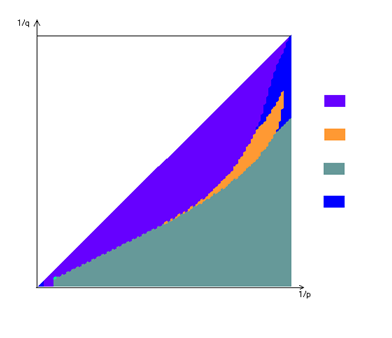
![]()
![Подпись: x[3]=x[4]=0.5 x[2]=0 x[5]=1 ](/images/referats/a44/132493/93.png)
![]()
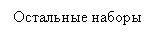
n=5
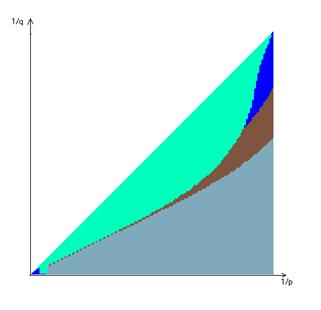
n=4
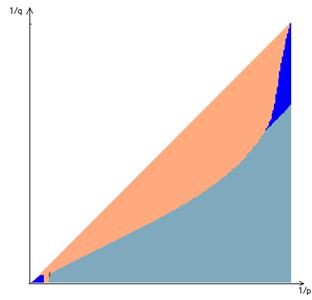
|
Приложение №5. Результаты работы программы №3.
p=2.000000 q=2.000000 max=0.707107
Nabor: x[0]=0.000000 x[1]=0.600000 x[2]=0.700000 x[3]=1.000000
p=2.000000 q=2.100000 max=0.696478
Nabor: x[0]=0.000000 x[1]=0.300000 x[2]=0.700000 x[3]=1.000000
p=2.000000 q=2.200000 max=0.686567
Nabor: x[0]=0.000000 x[1]=0.300000 x[2]=0.700000 x[3]=1.000000
p=2.000000 q=2.300000 max=0.677294
Nabor: x[0]=0.000000 x[1]=0.300000 x[2]=0.700000 x[3]=1.000000
p=2.000000 q=2.400000 max=0.668738
Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000
p=2.000000 q=2.500000 max=0.660879
Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000
p=2.000000 q=2.600000 max=0.653565
Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000
p=2.000000 q=2.700000 max=0.646741
Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000
p=2.000000 q=2.800000 max=0.640603
Nabor: x[0]=0.000000 x[1]=0.100000 x[2]=0.900000 x[3]=1.000000
p=2.000000 q=2.900000 max=0.635019
Nabor: x[0]=0.000000 x[1]=0.100000 x[2]=0.900000 x[3]=1.000000
Похожие работы
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...
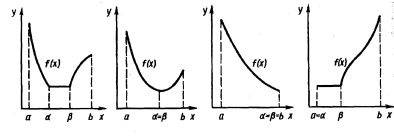
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...

0 комментариев