Навигация
Решение уравнений с помощью функции Find(x)
6.3 Решение уравнений с помощью функции Find(x)
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given – Find:
– задать начальное приближение
x:= х0
– ввести служебное слово
Given
– записать уравнение, используя знак жирное равно
![]()
– написать функцию find с неизвестной переменной в качестве параметра
find(x)=
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
Пример. Решение уравнения ![]() с помощью функции find представлено на рисунке 3.3.
с помощью функции find представлено на рисунке 3.3.
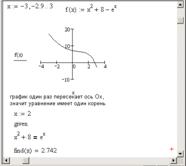
Рис. 3.3. Решение уравнения с помощью функции find
Иногда возникает необходимость отметить на графике какие-либо точки (например, точки пересечения функции с осью Ox). Для этого необходимо:
· указать значение x данной точки (по оси Ох) и значение функции в этой точке (по оси Оy);
· дважды щелкнуть по графику и в окне форматирования во вкладке Traces для соответствующей линии выбрать тип графика — points, толщину линии — 2 или 3.
Пример. На графике отмечена точка пересечения функции ![]() с осью Ох. Координата х этой точки была найдена в предыдущем примере: х = 2.742 (корень уравнения
с осью Ох. Координата х этой точки была найдена в предыдущем примере: х = 2.742 (корень уравнения ![]() ) (рис. 3.4).
) (рис. 3.4).

Рис. 3.4. График функции ![]() с отмеченной точкой пересечения
с отмеченной точкой пересечения
В окне форматирования графика во вкладке Traces для trace2 изменены: тип графика — points, толщина линии — 3, цвет — черный.
7. Решение систем уравнений 7.1 Решение систем линейных уравнений
Систему линейных уравнений можно решить матричным методом (или через обратную матрицу или используя функцию lsolve(A,B)) и с использованием двух функций Find и функции Minerr.
Матричный метод
Пример. Дана система уравнений:
![]() .
.
Решение данной системы уравнений матричным методом представлено на рисунке 4.1.

Рис. 4.1. Решение системы линейных уравнений матричным методом
Использование функции lsolve(A,B)
Lsolve(A,B) — это встроенная функция, которая возвращает вектор Х для системы линейных уравнений ![]() при заданной матрице коэффициентов А и векторе свободных членов В.
при заданной матрице коэффициентов А и векторе свободных членов В.
Пример. Дана система уравнений:
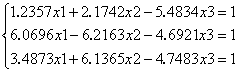 .
.
Способ решения данной системы с использованием функции lsolve(A,B) приведен на рисунке 4.2.

Рис. 4.2. Решение системы линейных уравнений с использованием функции lsolve
Решение системы линейных уравнений с помощью функции Find
При данном методе уравнения вводятся без использования матриц, т.е. в «натуральном виде». Предварительно необходимо указать начальные приближения неизвестных переменных. Это могут быть любые числа, входящие в область определения. Часто за них принимают столбец свободных членов.
Для того чтобы решить систему линейных уравнений с помощью вычислительного блока Given – Find, необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given;
3) записать систему уравнений, используя знак жирное равно(=);
4) написать функцию Find, перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
Пример. Дана система уравнений:
![]() .
.
Решение данной системы с помощью вычислительного блока Given – Find приведено на рисунке 4.3.

Рис. 4.3. Решение системы линейных уравнений с помощью функции Find
Приближенное решение системы линейных уравнений
Решение системы линейных уравнений с помощью функцию Minerr аналогично решению с помощью функции Find (используется тот же алгоритм), только функция Find дает точное решение, а Minerr — приближенное. Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке.
Общие рекомендации по решению уравнений и систем уравнений
Ниже перечислены некоторые рекомендации, которые следует выполнять, если MathCAD не может самостоятельно найти решение.
· Можно подобрать другое начальное приближение.
· Можно увеличить или уменьшить точность расчетов. Для этого в меню выбрать Math ► Options (Математика – Опции), вкладка Built-In Variables (Встроенные переменные). В открывшейся вкладке необходимо уменьшить допустимую погрешность вычислений (Convergence Tolerance (TOL)). По умолчанию TOL = 0.001.
Внимание. При матричном методе решения необходимо переставить коэффициенты согласно возрастанию неизвестных х1,х2, х3, х4.
7.2 Решение систем нелинейных уравненийСистемы нелинейных уравнений в MathCAD решаются с помощью вычислительного блока Given – Find.
Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Для решения системы уравнений с помощью блока Given – Find необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given;
3) записать систему уравнений, используя знак жирное равно(=);
4) написать функцию Find, перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
Если система имеет несколько решений, алгоритм следует повторить с другими начальными приближениями.
Примечание. Если решается система из двух уравнений с двумя неизвестными, перед решением желательно построить графики функций, чтобы проверить, есть ли корни у системы (пересекаются ли графики заданных функций), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
Пример. Дана система уравнений
![]() .
.
Перед решением системы построим графики функций: параболы (первое уравнение) и прямой (второе уравнение). Построение графика прямой и параболы в одной системе координат приведено на рисунке 4.5:

Рис. 4.5. Построение графика двух функций в одной системе координат
Прямая и парабола пересекаются в двух точках, значит, система имеет два решения. По графику выбираем начальные приближения неизвестных x и y для каждого решения. Нахождение корней системы уравнений представлено на рисунке 4.6.

Рис. 4.6. Нахождение корней системы нелинейных уравнений
Для того чтобы отметить на графике точки пересечения параболы и прямой, координаты точек, найденные при решении системы, введем по оси Ох (значения х) и по оси Оу (значения у) через запятую. В окне форматирования графика во вкладке Traces для trace3 и trace4 изменим: тип графика — points, толщина линии — 3, цвет — черный (рис. 4.7).
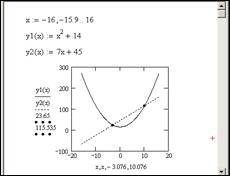
Рис. 4.7. Графики функций с отмеченными точками пересечения
8. Примеры использования основных возможностей MathCAD для решения некоторых математических задач
В данном разделе приведены примеры решения задач, для решения которых необходимо решить уравнение или систему уравнений.
8.1 Нахождение локальных экстремумов функцийНеобходимое условие экстремума (максимума и/или минимума) непрерывной функции формулируется так: экстремумы могут иметь место только в тех точках, где производная или равна нулю, или не существует (в частности, обращается в бесконечность). Для нахождения экстремумов непрерывной функции сначала находят точки, удовлетворяющие необходимому условию, то есть находят все действительные корни уравнения ![]() .
.
Если построен график функции, то можно сразу увидеть — максимум или минимум достигается в данной точке х. Если графика нет, то каждый из найденных корней исследуют одним из способов.
1-й способ. Сравнение знаков производной. Определяют знак производной ![]() в окрестности точки (в точках, отстоящих от экстремума функции по разные стороны на небольших расстояниях). Если знак производной при этом меняется от «+» к «–», то в данной точке функция имеет максимум. Если знак меняется от «–» к «+» , то в данной точке функция имеет минимум. Если знак производной не меняется, то экстремумов не существует.
в окрестности точки (в точках, отстоящих от экстремума функции по разные стороны на небольших расстояниях). Если знак производной при этом меняется от «+» к «–», то в данной точке функция имеет максимум. Если знак меняется от «–» к «+» , то в данной точке функция имеет минимум. Если знак производной не меняется, то экстремумов не существует.
2-й способ. Вычисление второй производной. В этом случае вычисляется вторая производная ![]() в точке экстремума. Если она меньше нуля, то в данной точке функция имеет максимум, если она больше нуля, то минимум.
в точке экстремума. Если она меньше нуля, то в данной точке функция имеет максимум, если она больше нуля, то минимум.
Пример. Нахождение экстремумов (минимумов/максимумов) функции ![]() .
.
Сначала построим график функции (рис. 6.1).

Рис. 6.1. Построение графика функции
Определим по графику начальные приближения значений х, соответствующих локальным экстремумам функции f(x). Найдем эти экстремумы, решив уравнение ![]() . Для решения используем блок Given – Find (рис. 6.2.).
. Для решения используем блок Given – Find (рис. 6.2.).

Рис. 6.2. Нахождение локальных экстремумов
Определим вид экстремумов первым способом, исследуя изменение знака производной в окрестности найденных значений (рис. 6.3).
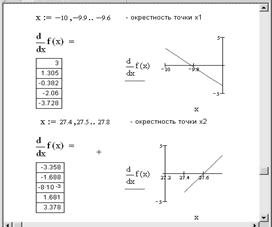
Рис. 6.3. Определение вида экстремума
Из таблицы значений производной и из графика видно, что знак производной в окрестности точки x1 меняется с плюса на минус, поэтому в этой точке функция достигает максимума. А в окрестности точки x2 знак производной поменялся с минуса на плюс, поэтому в этой точке функция достигает минимума.
Определим вид экстремумов вторым способом, вычисляя знак второй производной (рис. 6.4).

Рис. 6.4. Определение вида экстремума с помощью второй производной
Видно, что в точке x1 вторая производная меньше нуля, значит, точка х1 соответствует максимуму функции. А в точке x2 вторая производная больше нуля, значит, точка х2 соответствует минимуму функции.
Похожие работы
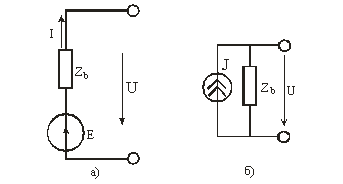
... – матрица проводимостей, обратная матрице сопротивлений ветвей. Если в функции fk и jk входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk и jk процессы в этой линейной или нелинейной электрической цепи ...
... один или несколько параметров. Параметры могут иметь численное значение, быть константой, ранее определенной переменной или математическим выражением, возвращающим численное значение. Рис.4. Окно выбора функции 2. Построение графика функции одного аргумента В Mathcad очень просто строить различные графики, которые в ряде случаев позволяют лучше понять особенности различных функциональных ...
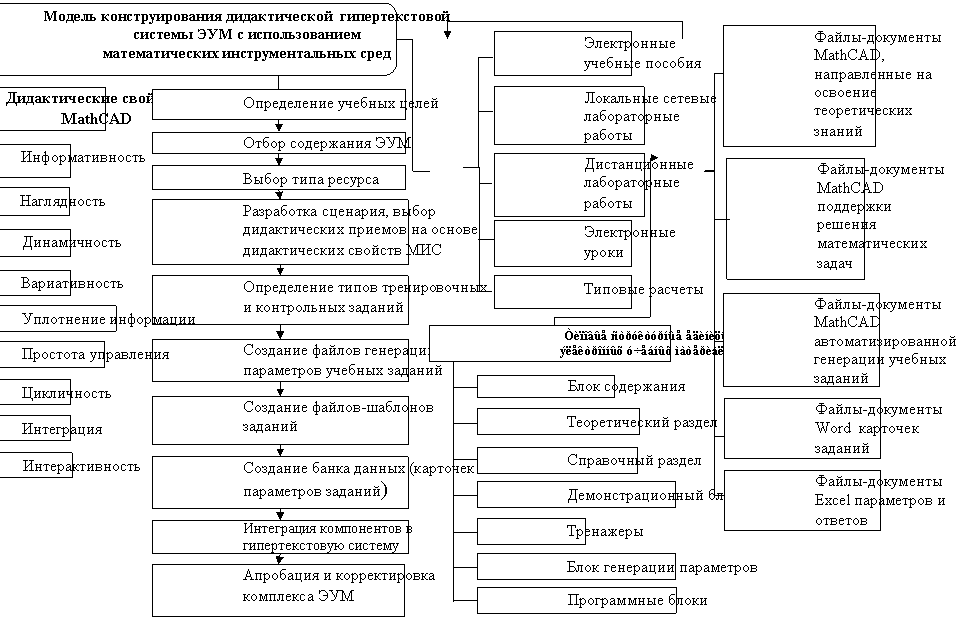
... системы электронных учебных материалов на основе технологии конструирования ЭУМ в среде MathCAD Происходит формирование умений и навыков конструирования электронных учебных материалов в среде MathCAD на творческом уровне В системе профессиональной подготовки учителей математики, физики, информатики недостаточно отражены подходы к созданию и применению электронных учебных материалов с ...
... , которая состоялась 22 февраля 1995 года, обсуждался ход реализации программы информатизации образования на 1994-1995 гг. Был рассмотрен вопрос о совершенствовании организации обучения информатике в общеобразовательной школе на современном этапе. Коллегия постановила признать целесообразной необходимость выделения нескольких этапов в овладении основами информатики и формировании информационной ...



0 комментариев