Навигация
Определение площадей фигур, ограниченных непрерывными линиями
8.2 Определение площадей фигур, ограниченных непрерывными линиями
Площадь криволинейной трапеции, ограниченной графиком функции f(x), отрезком [a,b] на оси Ox и двумя вертикалями х = а и х = b, a < b, определяется по формуле: ![]() .
.
Пример. Нахождение площади фигуры, ограниченной линиями f(x) = 1 – x2 и y = 0.

Рис. 6.5. Нахождение площади фигуры, ограниченной линиями f(x) = 1 – x2 и y = 0
Площадь фигуры, заключенной между графиками функций f1(x) и f2(x)и прямыми х = а и х = b, вычисляется по формуле:
| ! |
![]()
![]()
Внимание. Чтобы избежать ошибок при вычислении площади, разность функций надо брать по модулю. Таким образом, площадь будет всегда положительной величиной.
Пример. Нахождение площади фигуры, ограниченной линиями ![]() и
и ![]() . Решение представлено на рисунке 6.6.
. Решение представлено на рисунке 6.6.
1. Строим график функций.
2. Находим точки пересечения функций с помощью функции root. Начальные приближения определим по графику.
3. Найденные значения x подставляем в формулу ![]() как пределы интегрирования.
как пределы интегрирования.

Построение прямой, проходящей через две заданные точки
Для составления уравнения прямой, проходящей через две точки А(x0,y0) и B(x1,y1), предлагается следующий алгоритм:
1. Прямая задается уравнением y = ax + b,
где a и b — коэффициенты прямой, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
![]()
2. Данная система является линейной. В ней две неизвестные переменные: a и b. Систему можно решить матричным способом.
Пример. Построение прямой, проходящей через точки А(–2,–4) и В(5,7).
Подставим в уравнение прямой координаты данных точек и получим систему:
![]()
Решение этой системы в MathCAD представлено на рисунке 6.7.

Рис. 6.7.Решение системы
В результате решения системы получаем: а = 1.57, b = –0.857. Значит, уравнение прямой будет иметь вид: y = 1.57x – 0.857. Построим эту прямую (рис. 6.8).
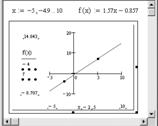
Рис. 6.8. Построение прямой
Построение параболы, проходящей через три заданные точки
Для построения параболы, проходящей через три точки А(x0,y0), B(x1,y1) и C(x2,y2), алгоритм следующий:
1. Парабола задается уравнением
y = ax2 + bх + с, где
а, b и с — коэффициенты параболы, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
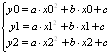 .
.
2. Данная система является линейной. В ней три неизвестные переменные: a, b и с. Систему можно решить матричным способом.
3. Полученные коэффициенты подставляем в уравнение и строим параболу.
Пример. Построение параболы, проходящей через точки А(–1,–4), B(1,–2) и C(3,16).
Подставляем в уравнение параболы заданные координаты точек и получаем систему:

Решение этой системы уравнений в MathCAD представлено на рисунке 6.9.

Рис. 6.9. Решение системы уравнений
В результате получены коэффициенты: a = 2, b = 1, c = –5. Получаем уравнение параболы: 2x2 +x –5 = y. Построим эту параболу (рис. 6.10).
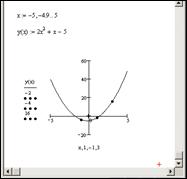
Рис. 6.10. Построение параболы
Построение окружности, проходящей через три заданные точки
Для построения окружности, проходящей через три точки А(x1,y1), B(x2,y2) и C(x3,y3), можно воспользоваться следующим алгоритмом:
1. Окружность задается уравнением
![]() ,
,
где x0,y0 — координаты центра окружности;
R — радиус окружности.
2. Подставим в уравнение окружности заданные координаты точек и получим систему:
 .
.
Данная система является нелинейной. В ней три неизвестные переменные: x0, y0 и R. Система решается с применением вычислительного блока Given – Find.
Пример. Построение окружности, проходящей через три точки А(–2,0), B(6,0) и C(2,4).
Подставим в уравнение окружности заданные координаты точек и получим систему:
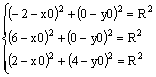
Решение системы в MathCAD представлено на рисунке 6.11.

Рис. 6.11. Решение системы
В результате решения системы получено: x0 = 2, y0 = 0, R = 4. Подставим полученные координаты центра окружности и радиус в уравнение окружности. Получим: ![]() . Выразим отсюда y и построим окружность (рис. 6.12).
. Выразим отсюда y и построим окружность (рис. 6.12).

Рис. 6.12. Построение окружности
Похожие работы
... – матрица проводимостей, обратная матрице сопротивлений ветвей. Если в функции fk и jk входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk и jk процессы в этой линейной или нелинейной электрической цепи ...
... один или несколько параметров. Параметры могут иметь численное значение, быть константой, ранее определенной переменной или математическим выражением, возвращающим численное значение. Рис.4. Окно выбора функции 2. Построение графика функции одного аргумента В Mathcad очень просто строить различные графики, которые в ряде случаев позволяют лучше понять особенности различных функциональных ...
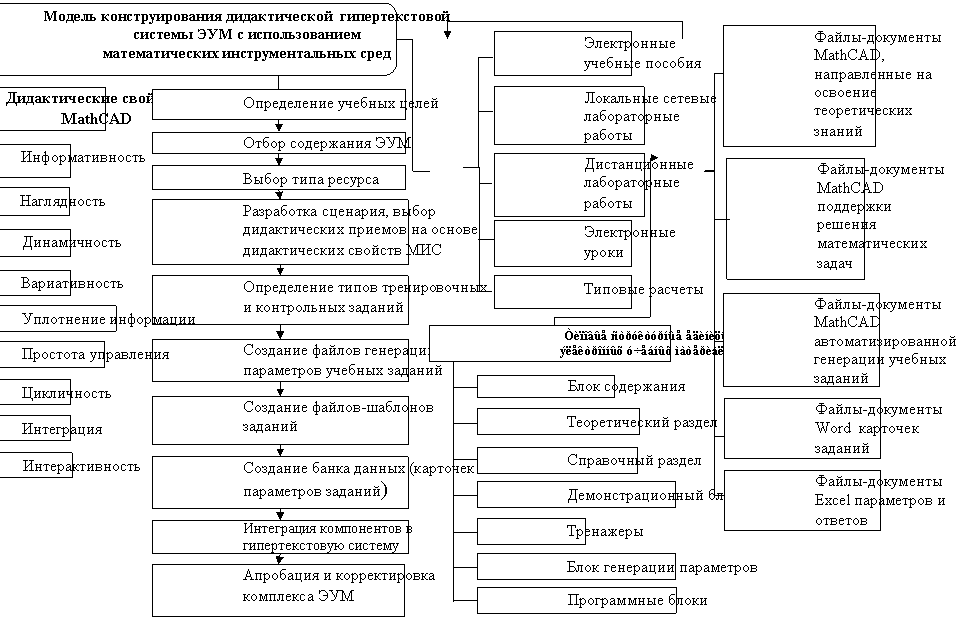
... системы электронных учебных материалов на основе технологии конструирования ЭУМ в среде MathCAD Происходит формирование умений и навыков конструирования электронных учебных материалов в среде MathCAD на творческом уровне В системе профессиональной подготовки учителей математики, физики, информатики недостаточно отражены подходы к созданию и применению электронных учебных материалов с ...
... , которая состоялась 22 февраля 1995 года, обсуждался ход реализации программы информатизации образования на 1994-1995 гг. Был рассмотрен вопрос о совершенствовании организации обучения информатике в общеобразовательной школе на современном этапе. Коллегия постановила признать целесообразной необходимость выделения нескольких этапов в овладении основами информатики и формировании информационной ...



0 комментариев