Навигация
Таблиця переходів автомата
2.1.2. Таблиця переходів автомата
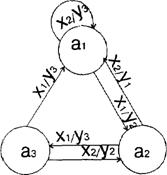
Для кожного стану ai визначаю по ГСА всі шляхи, які ведуть в інші стани і проходять обов’язково тільки через одні операторну вершину. Виняток становить перехід в кінцевий стан (вершину).
Для мікропрограмних автоматів таблиці переходів-виходів будуються у вигляді списку, тому що велика кількість станів. Розрізняють пряму та зворотну таблицю переходів. Зворотна таблиця переходів будується для D-тригера. Для автомата Мілі я буду будувати пряму таблицю переходів.
| Am Kam as Kas Xamas Yamas T1 T2 T3 T4 T5 | a1 10110 a2 10010 1 Y1Y4 T3 | a2 10010 | a4 | a6 00010 | 10000 X3 | X3 Y2Y6 | Y7 T1 | T4 | A | B | |
| a3 00011 a4 00010 1 Y2Y6 T5 | a4 00010 a5 00000 1 Y1Y8 T4 | a5 00000 a8 | a9 | a11 01000 | 01001 | 10001 X4 | X4X3 | X4X3 Y4 | Y3Y10 | Y6 | |
| T1 T2 | T2 | T5 | T5 C | D | E | a6 10000 a5 | a7 00000 | 11001 X1 | X1 Y1Y8 | ||
| Y5Y9 T1 | T2 | T5 F | G | a7 11001 a9 | a11 | a11 | a12 01001 | 10001 | 10001 | 11000 X4X3 | X4X3 |
| X4X1 | X4X1 Y3Y10 | Y6 | Y6 | Y2Y4 T1 | T2 | T2 | T5 H | I | |||
| J | K | a8 01000 a9 01001 1 Y4Y5 T5 | a9 01001 a10 00001 1 Y1Y2 T2 |
Табл.1. Таблиця переходів Т-тригера
2.1.3. Кодування станів
Аналіз канонічного методу структурного синтезу автомата показує, що різні варіанти кодування станів автомата приводять до різних виражень функцій збудження пам'яті і функцій виходів, у результаті чого складність комбінаційної схеми істотно залежить від обраного кодування.
Я буду кодувати стани автомату з допомогою евристичного алгоритму кодування, тому що я синтезую автомат на базі Т-тригера.
Даний алгоритм мінімізує сумарне число переключень елементів пам'яті на всіх переходах автомата і використовується для кодування станів автомата при синтезі на базі T, RS, JK-тригерів. Для даних типів тригерів (на відміну від D-тригерів) на кожнім переході, де тригер змінює своє значення на протилежне, одна з функцій збудження обов'язково дорівнює 1. Зменшення числа переключень тригерів приводить до зменшення кількості одиниць відповідних функцій збудження, що при відсутності мінімізації однозначно приводить до спрощення комбінаційної схеми автомата.
Будую матрицю |T|, яка складається із всіх пар номерів (i, j), для яких P(i, j) ¹ 0, ij. Для кожної пари вказуємо її вагу.
i j P(i, j)
1 2 1
2 4 1
2 6 1
3 4 1
4 5 1
5 8 1
5 9 1
5 10 1
5 11 1
6 5 1
6 7 1
7 9 1
7 11 2
7 12 1
8 9 1
9 10 1
10 3 1
10 7 1
10 4 1
10 5 1
T= 11 12 1
12 13 1
13 14 1
13 15 1
14 17 1
15 17 1
15 19 1
16 19 1
17 18 1
18 1 1
18 20 1
19 18 1
19 20 1
19 21 1
20 1 1
20 22 1
21 22 1
22 13 1
22 15 1
22 16 1
Далі, за допомогою програми ECODE 3, виконую кодування станів автомата на ЕОМ. При цьому вказую глибину кодування (від 4 до 6) та вибираю те кодування, коефіцієнт якого ближче до 1 (у мене коефіцієнт кодування 1,26). Результати кодування заношу до таблиці 1. Ось кінцеві результати кодування:
Підрахунок ефективності кодування:
Кількість переключень тригерів:
W = E P(i,j)*d(i,j) = P(1,2)*d(1,2) + P(1,18)*d(1,18) + P(1,20)*d(1,20) + +P(2,4)*d(2,4) + P(2,6)*d(2,6) + P(3,4)*d(3,4) + P(3,10)*d(3,10) + +P(4,5)*d(4,5) + P(4,10)*d(4,10) + P(5,6)*d(5,6) + P(5,8)*d(5,8) + +P(5,9)*d(5,9) + P(5,10)*d(5,10)+ P(5,11)*d(5,11) + P(6,7)*d(6,7) + +P(7,9)*d(7,9) + P(7,10)*d(7,10) + P(7,11)*d(7,11) + P(7,12)*d(7,12) + +P(8,9)*d(8,9) + P(9,10)*d(9,10) + P(11,12)*d(11,12) +P(12,13)*d(12,13) + +P(13,14)*d(13,14) + P(13,15)*d(13,15) + P(13,22)*d(13,22) +
+P(14,17)*d(14,17) + P(15,17)*d(15,17) + P(15,19)*d(15,19) + +P(15,22)*d(15,22) +P(16,19)*d(16,19) + P(16,22)*d(16,22) + +P(17,18)*d(17,18) + P(18,19)*d(18,19) +P(18,20)*d(18,20) + +P(19,20)*d(19,20) + P(19,21)*d(19,21) + P(20,22)*d(20,22) +
+P(21,22)*d(21,22) =
= 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*2 + 1*1 +1*1 + 1*2 + + 2*1 + 1*2 + 1*2 + 1*1 + 1*2 + 2*1 + 1*1 + 1*1 + 1*1 + 1*2 + 1*1 + 1*1 + +1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*2 + 1*2 + 2*1 + 1*1 + 1*1 + 1*2 + 1*1 + +1*1+ 1*2 + 1*2 = 53
Мінімальна можлива кількість переключень тригерів:
Wmin = E P(i,j) = 42
Коефіцієнт ефективності кодування: 1.26
Похожие работы
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
... y35 RS1:=Z1 y11 36 RS1 := RS2 + RS1 RS1 y26 RS2 y30 RS1+RS2 y40 RS1:=Z2 y10 Рис. 1.7 – Структурна граф-схема операційного автомата 2. СИНТЕЗ КЕРУЮЧИХ АВТОМАТІВ З ЖОРСТКОЮ ЛОГІКОЮ На практиці використовуються дві моделі МПА - автомат Милі й автомат Мура, розходження між якими полягає у функції ...
. 2002 Керівник: Ніколенко А.О. Прийняв до виконання: Ткаченко І.О. Зміст Завдання на розробку Зміст Синтез комбінаційної схеми Розрахування значень Мінімізація БФ Комбінаційна схема Проектування автоматів Вибір завдання Автомат Мура Автомат Мілі Заключення Перелік літератури 1 Синтез комбінаційної схеми 1.1 Визначення значень БФ Булева функція 5 змінних ...


0 комментариев