Навигация
Таблиця переходів автомата
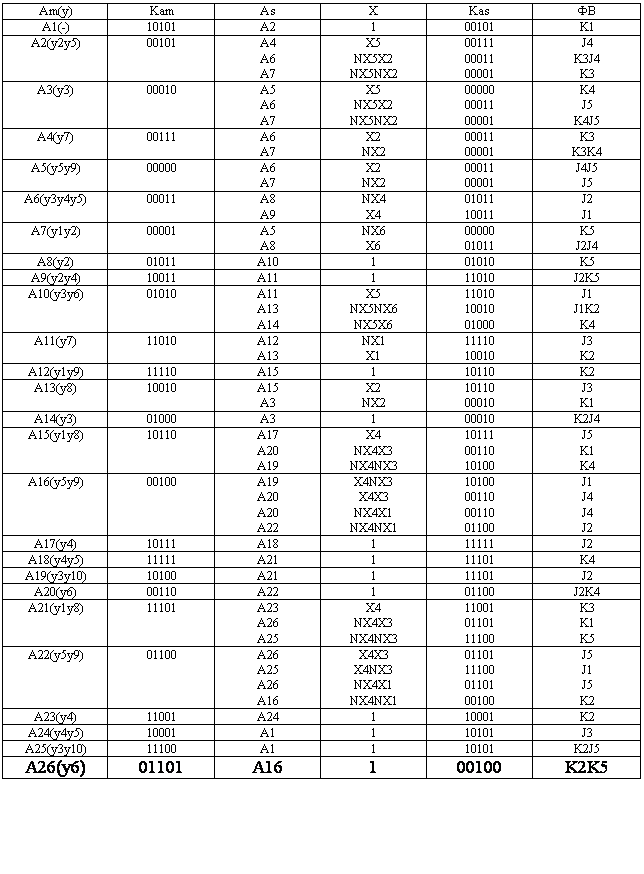
2.2.2. Таблиця переходів автомата
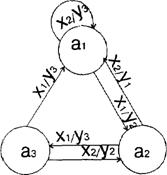
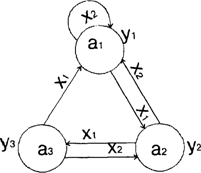
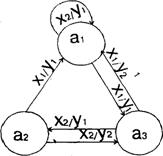
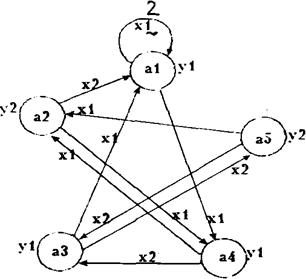
Для кожного стану ai визначаю по ГСА всі шляхи, які ведуть в інші стани і проходять обов’язково тільки через одні операторну вершину. Виняток становить перехід в кінцевий стан (вершину).
Для мікропрограмних автоматів таблиці переходів-виходів будуються у вигляді списку, тому що велика кількість станів. Розрізняють пряму та зворотну таблицю переходів. Зворотна таблиця переходів будується для D-тригера. Для автомата Мілі я буду будувати зворотну таблицю переходів.
Кодування станів
Кодування станів буде проводитися за таким алгоритмом:
1. Кожному стану автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm, рівне числу переходів у стан аm (Nm дорівнює числу появ аm у поле таблиці ).
2. Числа N1, N2, ..., Nm упорядковуються по убуванні.
3. Стан аs з найбільшим Ns кодується кодом: ![]() де R-кількість елементівпам'яті.
де R-кількість елементівпам'яті.
4. Наступні R станів згідно списку пункту 2 кодуються кодами, що містять тільки одну 1:00 ... 01, 00 ... 10, ... , 01 ... 00, 10 ... 00.
5. Для станів, що залишилися, знову в порядку списку п.2. використовують коди з двома одиницями, потім із трьома і так далі поки не будуть закодовані вес стани.
У результаті виходить таке кодування, при якому чим більше мається переходів у деякий стан, тим менше одиниць у його коді. Вираження для функцій збдження будуть простіше для D-тригерів, тому що функції порушення однозначно визначаються кодом стану переходу.
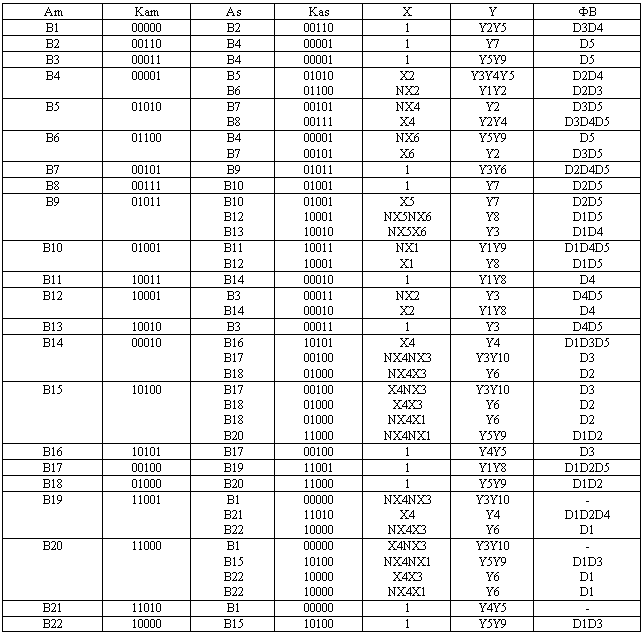
Табл.3. Таблиця переходів D-тригера
| Am | Kam | As | Kas | X | Y | ФЗ |
| A19 | 11110 | A1 | 00011 | NX1 | D4D5 | |
| A1 | 10110 | A2 | 00101 | 1 | Y5Y9 | D3 D5 |
| A21 | 00001 | A3 | 00110 | 1 | Y1Y8 | D3D4 |
| A3 | 00011 | A4 | 01010 | X4 | Y4 | D2 D4 |
| A3 A4 A2 | 00011 01010 00101 | A5 | 00000 | NX4NX3 1 X4NX3 | Y3Y10 Y4Y5 Y3Y10 | |
| A5 | 00010 | A6 | 01100 | 1 | Y1Y8 | D2D3 |
| A6 | 00000 | A7 | 10001 | X4 | Y4 | D1 D5 |
| A2 A2 A3 | 00110 00110 00011 | A8 | 00001 | X4X3 NX4NX1 NX4X3 | Y6 Y6 Y6 | D5 D5 D5 |
| A8 | 00111 | A9 | 10010 | 1 | Y5Y9 | D1 D4 |
| A6 A9 A9 | 00000 00101 00101 | A10 | 00010 | NX4X3 X4X3 NX4X1 | Y6 Y6 Y6 | D4 D4 D4 |
| A18 | 01111 | A11 | 10100 | NX5X6 | Y3 | D1 D3 |
| A10 | 00010 | A12 | 11000 | 1 | Y1Y8 | D1D2 |
| A11 | 01011 | A13 | 00111 | 1 | Y5Y9 | D3D4D5 |
| A12 | 01100 | A14 | 01011 | X4 | Y4 | D2 D4D5 |
| A14 A12 A13 | 01110 01100 01001 | A15 | 00100 | 1 NX4NX3 X4NX3 | Y4Y5 Y3Y10 Y3Y10 | D3 D3 D3 |
| A12 A13 A13 | 01100 01001 01001 | A16 | 10000 | NX4X3 X4X3 NX4X1 | Y6 Y6 Y6 | D1 D1 D1 |
| A15 | 01000 | A17 | 01110 | 1 | Y2Y4 | D2D3D4 |
| A16 | 01101 | A18 | 10011 | 1 | Y3Y6 | D1 D4 |
| A17 | 11000 | A19 | 10101 | 1 | Y7 | D1 D3 D5 |
| A19 A18 | 11110 01111 | A20 | 01001 | X1 NX5NX6 | Y8 Y8 | D2 D5 D2 D5 |
| A7 A6 A9 | 10000 00000 00101 | A21 | 01000 | 1 NX3NX4 NX4X3 | Y4Y5 Y3Y10 Y3Y10 | D2 D2 D2 |
Для підвищення функціональності схеми можна виділити однакові елементи:
Виписуємо з таблиці вирази для тригерів (та виконуємо необхідні перетворення для представлення їх в рамках потрібної серії):
Вихідні стани автомата Мілі:
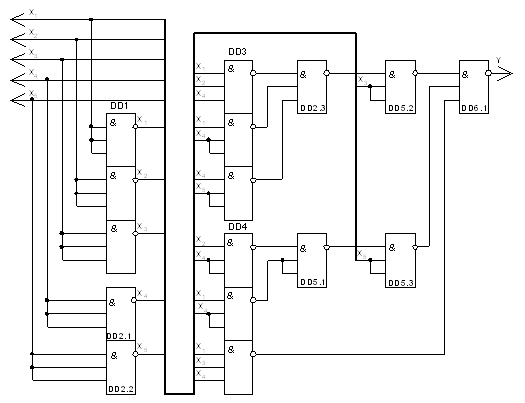
Ми отримали усі необхідні вирази для принципової схеми. Будуємо її, користуючись формулами для тригерів та вихідними станами (Лист 2).
Заключення
В ході проекту ми отримали комбінаційну схему булевої функції в заданому базисі та побудували принципову схему керуючого автомата Мура.
Синтез автомата був виконаний з урахуванням серії КР1533, тому може бути зроблений та опробований в реальному житті. В цілому курсова робота довела свою важливість у закріпленні отриманих знань та набутті низки звичок щодо проектування цифрових автоматів.
Перелік використаної літератури
1. Методичні вказівки до курсової роботи по дисципліні “Прикладна теорія цифрових автоматів”. Одеса. ОГПУ. 1998р.
2. Мікросхеми серії 1533(555). Стислі теоретичні дані. Одеса. Центр
НТТМ ОГПУ. 1975г.
3. ГОСТ 2.708-81 ЄСКД. Правила виконання електричних схем цифрової обчи слювальної техніки.
4. ГОСТ 2.743-82. ЄСКД. Умовні графічні позначення в схемах. Елементи цифрової техніки.
Похожие работы
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
... y35 RS1:=Z1 y11 36 RS1 := RS2 + RS1 RS1 y26 RS2 y30 RS1+RS2 y40 RS1:=Z2 y10 Рис. 1.7 – Структурна граф-схема операційного автомата 2. СИНТЕЗ КЕРУЮЧИХ АВТОМАТІВ З ЖОРСТКОЮ ЛОГІКОЮ На практиці використовуються дві моделі МПА - автомат Милі й автомат Мура, розходження між якими полягає у функції ...
. 2002 Керівник: Ніколенко А.О. Прийняв до виконання: Ткаченко І.О. Зміст Завдання на розробку Зміст Синтез комбінаційної схеми Розрахування значень Мінімізація БФ Комбінаційна схема Проектування автоматів Вибір завдання Автомат Мура Автомат Мілі Заключення Перелік літератури 1 Синтез комбінаційної схеми 1.1 Визначення значень БФ Булева функція 5 змінних ...


0 комментариев