Навигация
Работа с финансовыми функциями Excel
В пакете EXCEL встроены специальные функции для проведения различных финансово-экономических расчетов. Осуществляется выбор функции с помощью кнопки "Вставка функции" на панели инструментов, категория - "Финансовые".
Определение будущей стоимости
Будущая стоимость текущего значения вклада при постоянной процентной ставке рассчитывается с помощью функции:
Б3 (норма; число_периодов; выплата; нз; тип),
где:
норма - процентная ставка за один период;
число _периодов - общее число периодов выплат;
выплата - это выплата, производимая в каждый период, это значение не может меняться в течение всего периода выплат, обычно выплата состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов;
нз - текущая стоимость вклада (настоящее значение), если аргумент нз опущен, то он полагается равным 0;
тип - это число 0 или 1, обозначающее, когда производится выплата (1 - в начале периода, 0-в конце периода). Если аргумент тип опущен, то он полагается равным 0. Параметр тип нужно указывать только тогда, когда выплата не равна 0, т.е. делаются взносы по периодам.
Задание 1.1. На сберегательный счет в конце каждого месяца вносятся обязательные платежи по 100 тыс. грн. Рассчитайте, какая сумма окажется на счете через восемь лет при ставке процента 9.5% годовых.
Решение:
Для расчета применяется формула БЗ, т.к требуется найти будущее значение выплаченной суммы. В данной задаче при ежемесячном начислении процентов общее число периодов начисления равно 8*12 (аргумент число_периодов), а процент за период начисления равен 9,5%/12 (аргумент норма). По условию аргумент нз = - 100000. Это отрицательна сумма, т.к деньги были вложены. Выплаты отсутствую, поэтому аргумент выплата отсутствует. Используя функцию БЗ, получим
Б3 (9,5%/12; 8*12;; - 1000000) = 14297518,58 грн.
Результаты решения задачи представлены в таблице 1.
Динамика роста стоимости показана в рисунке 2.
Таблица 3 содержит расчетные формулы к решению задачи в пакете Microsoft Excel.
Таблица 1
Расчет будущей стоимости
| A | B | C | D | E | F | G | |
| 1 | ЗАДАНИЕ №1 | ||||||
| 2 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 3 | 1 | 0,007917 | 12 | -100000 | 0 | 0 | 1 253 653,69р. |
| 4 | 2 | 0,007917 | 24 | -100000 | 0 | 0 | 2 631 729,49р. |
| 5 | 3 | 0,007917 | 36 | -100000 | 0 | 0 | 4 146 575,97р. |
| 6 | 4 | 0,007917 | 48 | -100000 | 0 | 0 | 5 811 767,32р. |
| 7 | 5 | 0,007917 | 60 | -100000 | 0 | 0 | 7 642 224,88р. |
| 8 | 6 | 0,007917 | 72 | -100000 | 0 | 0 | 9 654 350,92р. |
| 9 | 7 | 0,007917 | 84 | -100000 | 0 | 0 | 11 866 175,62р. |
| 10 | 8 | 0,007917 | 96 | -100000 | 0 | 0 | 14 297 518,58р. |
Рисунок 2
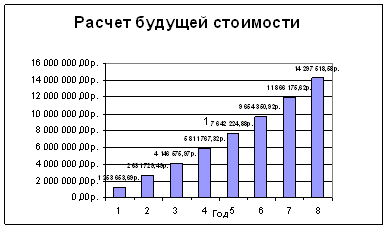
Таблица 3. Расчет будущей стоимости
| A | B | C | D | E | F | G | |
| 1 | ЗАДАНИЕ №1 | ||||||
| 2 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 3 | 1 | =0,095/12 | =12*A3 | -100000 | 0 | 0 | =БЗ (B3; C3; D3; 0; F3) |
| 4 | 2 | =0,095/12 | =12*A4 | -100000 | 0 | 0 | =БЗ (B4; C4; D4; 0; F4) |
| 5 | 3 | =0,095/12 | =12*A5 | -100000 | 0 | 0 | =БЗ (B5; C5; D5; 0; F5) |
| 6 | 4 | =0,095/12 | =12*A6 | -100000 | 0 | 0 | =БЗ (B6; C6; D6; 0; F6) |
| 7 | 5 | =0,095/12 | =12*A7 | -100000 | 0 | 0 | =БЗ (B7; C7; D7; 0; F7) |
| 8 | 6 | =0,095/12 | =12*A8 | -100000 | 0 | 0 | =БЗ (B8; C8; D8; 0; F8) |
| 9 | 7 | =0,095/12 | =12*A9 | -100000 | 0 | 0 | =БЗ (B9; C9; D9; 0; F9) |
| 10 | 8 | =0,095/12 | =12*A10 | -100000 | 0 | 0 | =БЗ (B10; C10; D10; 0; F10) |
Определение текущей стоимости.
Для расчета текущей стоимости (начальное значение) вклада (займа) используется функция
П3 (норма; Кпер; выплата; бс; тип),
где:
норма - процентная ставка за один период;
Кпе - общее число периодов выплат;
выплата - это выплата, производимая в каждый периода
бс - будущая стоимость вклада, которую нужно достичь после последней выплаты, если аргумент бс опущен, то он полагается равным 0;...
тшп - это число 0 или 1, обозначающее, когда производится выплата (1 - в начале периода, 0 - в конце периода), если аргумент пшп опущен, то он полагается равным 0. Параметр mип нужно указывать, только если выплата не равна 0, т.е. делаются взносы по периодам.
Задание 1.2 Какую сумму необходимо положить на депозит под 16% годовых, чтобы получить через четыре года 25 млн. грн. при ежеквартальном начислении процентов?
Решение
Для расчета используем функцию ПЗ.
При этом норма = 16%, Кпер =4, выплата = 2500000 грн., бс = 0.
П3 (16; 4; 2500000;) = - 13 347 704,39р. грн.
Результаты решения задачи представлены в таблице 4. Динамика роста стоимости показана в рисунке 5. Таблица 6 содержит расчетные формулы к решению задачи в пакете Microsoft Excel.
Таблица 4
Текущая стоимость
| A | B | C | D | E | F | G | |
| 31 | ЗАДАНИЕ №2 | ||||||
| 32 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 33 | 1 | 16% | 4 | 0 | 25000000 | 0 | -21370104,78р. |
| 34 | 2 | 16% | 8 | 0 | 25000000 | 0 | -18267255,13р. |
| 35 | 3 | 16% | 12 | 0 | 25000000 | 0 | -15614926,24р. |
| 36 | 4 | 16% | 16 | 0 | 25000000 | 0 | -13347704,39р. |
Рисунок 5
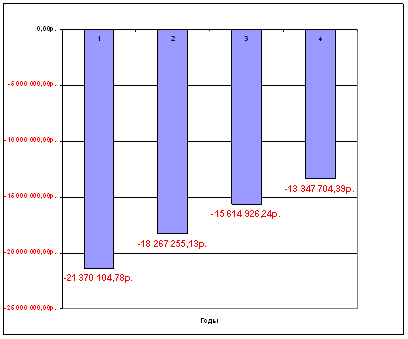
Таблица 6
Текущая стоимость
| A | B | C | D | E | F | G | |
| 28 | ЗАДАНИЕ №2 | ||||||
| 29 | год | ставка | число периодов | выплата | вклад | тип | величина вклада |
| 30 | 1 | 16% | =4*A30 | 0 | 25000000 | 0 | =ПЗ (B30/4; C30; D30; E30; F30) |
| 31 | 2 | 16% | =4*A31 | 0 | 25000000 | 0 | =ПЗ (B31/4; C31; D31; E31; F31) |
| 32 | 3 | 16% | =4*A32 | 0 | 25000000 | 0 | =ПЗ (B32/4; C32; D32; E32; F32) |
| 33 | 4 | 16% | =4*A33 | 0 | 25000000 | 0 | =ПЗ (B33/4; C33; D33; E33; F33) |
Цель экономического регрессионного анализа - на основе собранных статистических данных, которые представлены в виде таблицы, найти экономическую модель и произвести на основе этой модели соответствующие экономические расчеты и прогнозы.
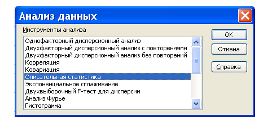
Для построения корреляционного поля необходимо выполнить следующие действия:
Открыть рабочее окно EXCEL и ввести значения данных х и у.
Построить точечную диаграмму.
Выполнить пункты меню Диаграмма - Добавить линию тренда. На вкладке Тип выбрать тип диаграммы, (линейная, логарифмическая, полиноминальная, степенная, экспоненциальная).
Обратить внимание на то, что в различных вариантах зависимость может быть любого из перечисленных видов. Далее выбрать вкладку Параметры и поставить " ٧ " в окне Показать уравнение на диаграмме.
Сделать вывод о виде принятой гипотезы.
Задание. Произвести экономический анализ для заданных статистических данных. Сделать выбор.
| X | 5,21 | 5,61 | 6,12 | 6,61 | 7,01 | 7,59 | 7,98 | 8,48 | 8,99 | 10,49 |
| Y | 13,4 | 14,12 | 15,34 | 16,52 | 17,02 | 17,78 | 19,06 | 19,96 | 20,78 | 23,98 |
Решение
Выполняем построение точечной диаграммы и добавляем линию трейда с различными типами диаграммы:
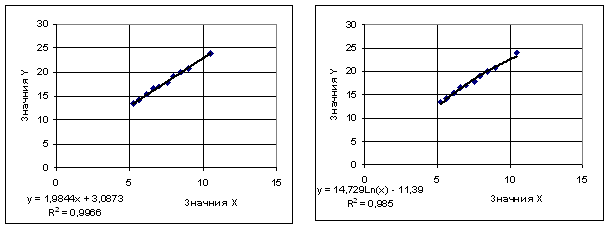 - линейная – логарифмическая
- линейная – логарифмическая
- полиноминальная – степенная, экспоненциальная
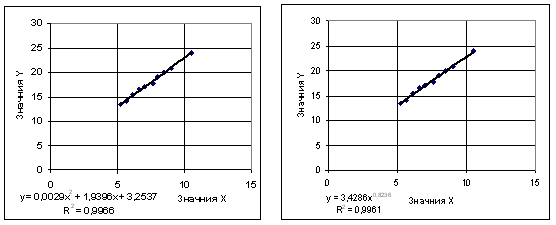
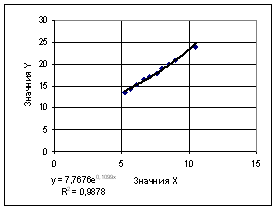
Вывод: проанализировав величину коэффициента достоверности аппроксимации R2 для каждого типа зависимости можно сделать вывод, что исходные экономические данные можно аппроксимировать с наибольшей точностью линейной зависимостью y = 1,9844x + 3,0873 и полиномиальной зависимостью у = 0,0029x2 + +1,9396x + 3,2537, так как R2 = 0,99966.
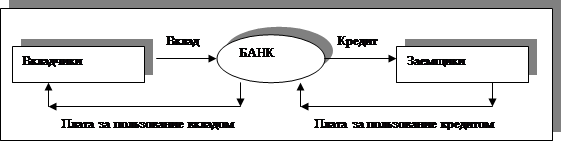
Задача №3. Модель Леонтьева многоотраслевой экономики (балансовый анализ)Одной из основных задач, возникающих в макроэкономике, является задача, связанная с эффективностью ведения многоотраслевого хозяйства; каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой - как потребитель продукции и своей, и произведенной другими отраслями.
Введем следующие обозначения:
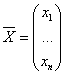 -вектор валового выпуска;
-вектор валового выпуска;
хy - объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства;
 -вектор конечного продукта;
-вектор конечного продукта;
 - матрица прямых затрат, коэффициенты прямых затрат вычисляются по формуле
- матрица прямых затрат, коэффициенты прямых затрат вычисляются по формуле ![]() .
.
Основная задача межотраслевого баланса - отыскание такого вектора валового выпуска ![]() , который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта
, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта ![]() .
.
Матричное решение данной задачи:
![]()
Работа с матрицами s пакете Excel
В пакете Excel существует несколько функций для работы с матрицами:
ТРАНСП - транспонирование матрицы;
МОПРЕД - нахождение определителя матрицы;
МУМНОЖ - умножение матриц;
МОБР - нахождение обратной матрицы.
Все эти функции (кроме ТРАНСП) находятся в категории "Математические", функция ТРАНСП - в категории "Ссылки и массивы".
Для работы с матрицами необходимо сделать следующее:
1 Выделить блок ячеек, в который нужно поместить результат.
2 Выбрать Вставка функции, найти нужную функцию.
3 Ввести адрес (или адреса) исходной матрицы (непосредственно или курсором). Нажать кнопку "ОК".
Для того, чтобы получить на экране все значения результата, нажать клавиши F2 и одновременно Ctrl+Shift+Enter.
Задание
Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором Y. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и формулами.
Решение:
1. Вводим исходные данные в ячейки пакета Excel. Матрицу прямых затрат А вводим в ячейки (B2: D4), матрицу спроса ![]() в ячейки (G2: G4).
в ячейки (G2: G4).

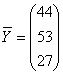
2. Определим матрицу прямых затрат ![]() . Вначале найдем матрицу (Е-А).
. Вначале найдем матрицу (Е-А).
Где Е - единичная матрица,
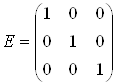 .
.
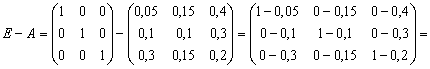
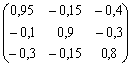 .
.
Вводим в ячейки (B6: D8) единичную матрицу. Матрицу (Е-А) посчитаем в ячейках (B13: D15) по формуле
![]() .
.
Похожие работы
... , согласно таблице порядковых номеров дней: . Подставим полученное значение t формулу (*): б). Для вычисления точных процентов с точным числом дней ссуды используем функцию Excel ДОЛЯГОДА: = А5*ДОЛЯГОДА (C5;D5;1)*G5 (см. приложение 1 таб. 3). 2б. Для вычисления обыкновенных процентов с точным числом дней ссуды применим функцию Excel ДОЛЯГОДА: = А5*ДОЛЯГОДА (C5;D5;2)*G5 (см. приложение 1 ...
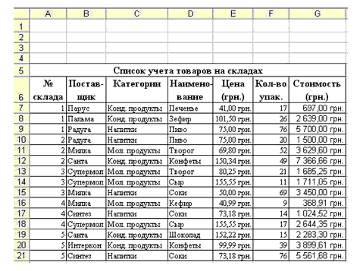
... средство, которое называется проверкой ввода (команда Проверка). При создании списка необходимо выполнить определенные требования: · Чтобы редактор автоматически распознавал список как базу данных и обрабатывал данные при выполнении команд обработки необходимо на рабочем листе располагать один список; · Формат шрифта заголовков (подписей) столбцов или имен полей в ...
... -функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но ...
... ячейка существует специальная команда меню Формат=>Ячейки, либо соответствующая команда контекстного меню. Диалоговое окно Формат ячеек имеет несколько вкладок. 3.1 Режимы работы табличного процессора Режим, в котором находится табличный процессор в каждый конкретный момент, отражается в Строке состояния (внизу окна, слева). 1) режим готовности - в Строке состояния появляется ...

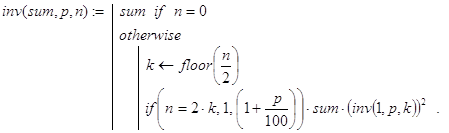
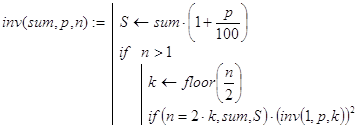
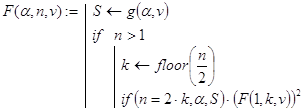
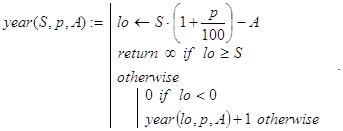
0 комментариев