Навигация
3.2 Задача 3.2 (вар. №6)
Скоротити слідуючи дроби
![]()
Розв’язання.
> (a^5+a^4+a^3+a^2+a+1)/((a^2+a+1)*(a+1));
![]()
Чисельник вихідного дробу позначимо через v1
> v1:=a^5+a^4+a^3+a^2+a+1;
![]()
Розкладаємо чисельник v1 на множники
> v1:=factor(v1);
![]()
Знаменник вихідного дробу позначимо через v2
> v2:=(a^2+a+1)*(a+1);
![]()
Скорочуємо чисельник v1 та знаменник v2
> v3:=v1/v2;
![]()
Відповідь: ![]()
4. Завдання №4
4.1 Задача 4.1 (вар. №6)
Розв’язати рівняння 1-й степені
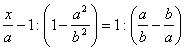
Розв’язання.
Використовуємо встроені функції елементарних перетворень пакету MAPLE: solve(рівняння або нерівність, змінна),
> ((x/a)-1)/(1-a^2/b^2)=1/(a/b-b/a);
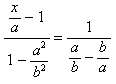
Задаємо рівняння eq
> eq:=((x/a)-1)/(1-a^2/b^2)-1/(a/b-b/a)=0;
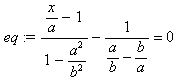
Розв'язуємо рівняння eq відносно змінної x
> solve(eq,{x});
![]()
Зробимо перевірку: підставляємо у вихідне рівняння eq розв'язок x і одержуємо тотожність
> subs(x=-(-b+a)*a/b,((x/a)-1)/(1-a^2/b^2)-1/(a/b-b/a));
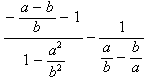
Спрощуємо останній вираз (останній результат Maple зберігає під ім’ям %)
> simplify(%);
![]()
Відповідь: ![]()
4.2 Задача 4.2 (вар. №6)
Розв’язати рівняння 1-й степені
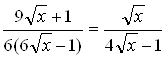
Розв’язання.
> (9*sqrt(x)+1)/(6*(6*sqrt(x)-1))=sqrt(x)/(4*sqrt(x)-1);
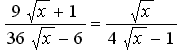
Задаємо рівняння eq
> eq:=(9*sqrt(x)+1)/(6*(6*sqrt(x)-1))-sqrt(x)/(4*sqrt(x)-1)=0;
![]()
Розв'язуємо рівняння eq відносно змінної x
> solve(eq,{x});
![]()
Зробимо перевірку: підставляємо у вихідне рівняння eq розв'язок x і одержуємо 0
> subs(x=1,(9*sqrt(x)+1)/(6*(6*sqrt(x)-1))-sqrt(x)/(4*sqrt(x)-1));
![]()
Відповідь: 1.
5. Завдання №5
5.1 Задача 5.1 (вар. №6)
Розв’язати системи рівнянь з двома невідомими
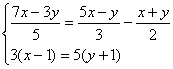
Розв’язання.
Використовуємо встроені функції елементарних перетворень пакету MAPLE: solve(рівняння або нерівність, змінна).
> (7*x-3*y)/5=(5*x-y)/3-(x+y)/2;3*(x-1)=5*(y+1);
![]()
![]()
Задаємо систему рівнянь з двома невідомими
> sistema:={(7*x-3*y)/5=(5*x-y)/3-(x+y)/2, 3*(x-1)=5*(y+1)};
![]()
Розв'язуємо систему рівнянь відносно x,y
> s:=solve(sistema,{x,y});
![]()
Зробимо перевірку: підставляємо у вихідну систему розв’язок і одержуємо дві тотожності
> eval(sistema,s);
![]()
Відповідь: (1; 1).
5.2 Задача 5.2 (вар. №6)
Розв'язати системи рівнянь з двома невідомими
![]()
Розв’язання.
> (x+2*y-7)/(2*y-x+15)/(2*x+y+19)=1/2/3;(3*x+y-3)/(4*x-2*y+1)/(5*x-3*y+8)= 6/3/5;
![]()
![]()
Задаємо систему рівнянь
> sistema:={(x+2*y-7)/(3*x+y-3)=t/6, (2*y-x+15)/(4*x-2*y+1)=2*t/3, (2*x+y+19)/(5*x-3*y+8)=3*t/5};
![]()
Розв'язуємо систему рівнянь відносно змінних x,y,t
> s:=solve(sistema,{x,y,t});
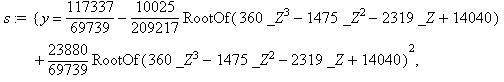
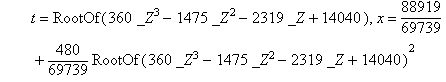
![]()
Для подання результів розв'язання системи рівнянь Maple використовує спеціальну функцію RootOf( ), яка застосовується для позначення будь-якого кореня виразу, заданого як її параметр. Змінна _Z - системна змінна, згенерована Maple, яка набуває цілих значень. За допомогою функції eval( ) можна отримати наближені числові значення функції RootOf( ).
> evalf(s);
![]()
6. Завдання №6
6.1 Задача 6.1 (вар. №6)
Побудувати графіки наступних функцій
![]()
Розв’язання.
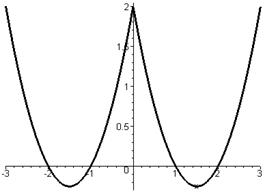
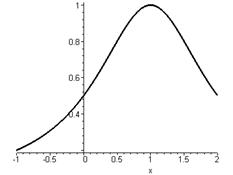
> f:=x^2-3*abs(x)+2;
![]()
Будуємо графік функції f, обираємо проміжок для змінної x від -3 до 3, колір - синій, товщина лінії – 3
> plot(f,x=-3..3,color=blue,thickness=3);
6.2 Задача 6.2 (вар. №6)
Побудувати графіки наступних функцій
![]()
Розв’язання.
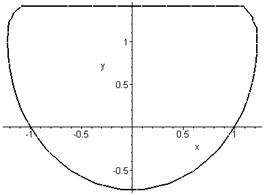
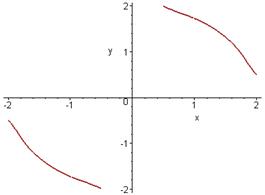
> y-x^2-y^2+2-abs(y-x^2)=0;
![]()
Будуємо графік функції, заданої неявно за допомогою пакету plots
> with(plots):implicitplot(y-x^2-y^2+2-abs(y-x^2),x=-3..3,y=-1..2, color=black, thickness=2);
7. Завдання №7
7.1 Задача 7.1 (вар. №6)
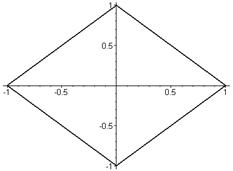
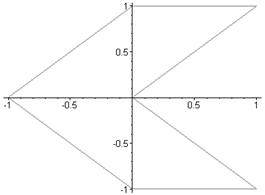
Зобразити наступні геометричні фігури згідно ескізу рис. 7.1 вихідних даних.
Розв’язання.
Використаємо пакет plottools – пакет для створення та роботи з графічними об’єктами. Команда curve([[x1,y1],[x2,y2],…,[xn,yn],options) задає криву координатами своїх точок. Крива відображається лінійними сегментами, що з’єднують сусідні точки. Команда display відображає вивід графічних команд на екран.
> with(plottools): w:=curve([[1,0],[0,1],[-1,0],[0,-1],[1,0]],color=black, linestyle=1, thickness=2): plots[display](w);
7.2 Задача 7.2 (вар. №6)
Зобразити наступні геометричні фігури згідно ескізу рис.7.2 вихідних даних.
Розв’язання.
> with(plottools): u:=curve([[0,0],[1,-1],[0,-1],[-1,0],[0,1],[1,1],[0,0]],color=green, linestyle=1, thickness=2): plots[display](u);
Похожие работы
і дані завдань варіанту №7 1. Завдання №1 1.1 Задача 1.1 (вар. №7) Спростити вираз Розв’язання. Алгебраїчні перетворення в Maple проводяться за допомогою вбудованих функцій елементарних перетворень таких як simplify - спростити, expand - розкрити дужки, factor -розкласти на множники, normal - привести до спільного знаменника, combine-перетворення ступеня, collect- ...
... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... САПР? 14. Які основні принципи створення САПР Вам відомі? 15. Які види САПР Вам відомі? 16. Які функції повинні виконувати інтегровані САПР? 17. Назвіть основні особливості технології автоматизованого проектування. 18. Який комплекс вимог пред'являє до САПР реалізація технології автоматизованого проектування? 19. Назвіть найбільш характерні відмітні особливості ГСАПР. 20. Дайте ...


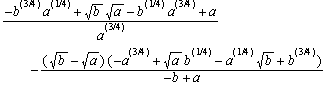


0 комментариев