Керівництво оператору

5. Керівництво оператору

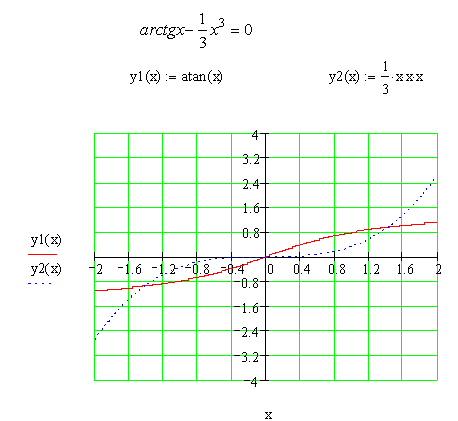
Для завантаження програми необхідно запустити програмний файл Project1.exe. При цьому з’явиться вікно (рис. 1), де можна задати початкові умови, переглянути постановку задачі а також ознайомитися з розв’язком при натисненні кнопки Розв’язок.

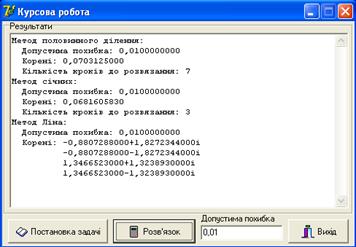
Рисунок 1. Інтерфейс програми.

6. Результати обчислень

 

Метод половинного ділення:

Допустима похибка: 0,0100000000

Корені: 0,0703125000

Кількість кроків до розв’язання: 7

Метод січних:

Допустима похибка: 0,0100000000

Корені: 0,0681605830

Кількість кроків до розв’язання: 3

Метод Ліна:

Допустима похибка: 0,0100000000

Корені: -0,8807288000+1,8272344000i

-0,8807288000-1,8272344000i

1,3466523000+1,3238930000i

1,3466523000-1,3238930000i

Висновки

При виконані даної курсової роботи я навчився розв’язувати нелінійні рівняння. Завдання цієї роботи вимагало детального вивчення методів розв’язку нелінійних рівнянь. Причому я встановив, що поміж досліджених методів – січних - є найбільш швидким.

Література

1. Самарський А.А. Вступ в чисельні методи. - М.: Наука, 1987. – 286 с.

2.Квєтний Р.Н., Маліков В.Т. Обчислювльні методи та використання ЕОМ. Вища школа, 1989 – 55 с., 104 с.

Додаток A

 

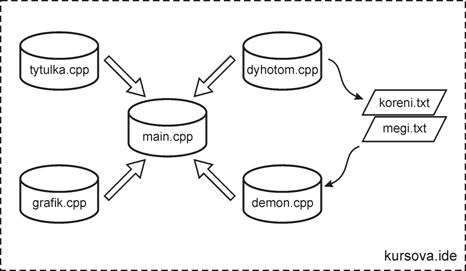
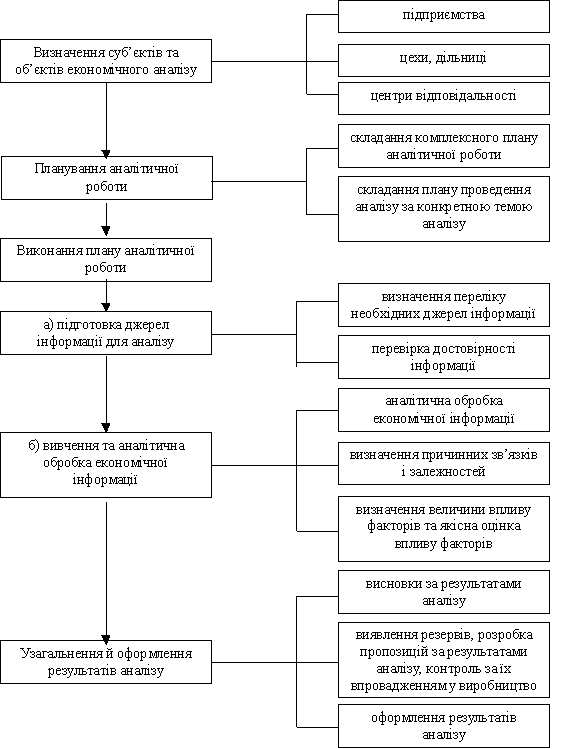
Алгоритм роботи програми

Задання початкових умов

Додаток Б

 

Лістинг програми

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, ExtCtrls, Buttons, Math;

type

TForm1 = class(TForm)

GroupBox2: TGroupBox;

BitBtn1: TBitBtn;

BitBtn2: TBitBtn;

BitBtn3: TBitBtn;

Memo1: TMemo;

LabeledEdit1: TLabeledEdit;

procedure BitBtn1Click(Sender: TObject);

procedure BitBtn2Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

const

v:array [0..5] of Extended = (-1,15,-5,3,-1,1);

implementation

uses Unit2;

{$R *.dfm}

procedure TForm1.BitBtn1Click(Sender: TObject);

begin

Form2.ShowModal;

end;

procedure TForm1.BitBtn2Click(Sender: TObject);

function f(x:Extended):Extended;

var

i:integer;

begin

result:=v[5]*x*x*x*x*x+v[4]*x*x*x*x+v[3]*x*x*x+v[2]*x*x+v[1]*x+v[0];

end;

const

n = 5;

var

step, j, i,k :integer;

err:Extended;

x,y:Extended;

x_l, x_r, p,q, pp, qq,t: Extended;

b:array[0..n+1] of Extended;

a:array[0..n-1,0..n-1] of Extended;

begin

try

// Half-dividing method

x_l := 0; x_r := 1;

step := 0; y:=f(x_l);

err:=StrToFloat(LabeledEdit1.Text);

while abs(x_l-x_r)>err do begin

x:=(x_r+x_l)/2;

if f(x_l)*f(x)>0 then

x_l := x

else

x_r := x;

y:=f(x);

inc(step);

end;

with Memo1.Lines do begin

Clear;

Add('Метод половинного д_лення:');

Add(' Допустима похибка: '+FloatToStrF(err,ffFixed,8,10));

Add(' Корен_: '+FloatToStrF(x,ffFixed,8,10));

Add(' К_льк_сть крок_в до розвязання: '+IntToStr(step));

end;

// Trunc's method

x := 1; x_l := 0;

step := 0;

while abs(x_l-x)>err do begin

x_l := x;

x := x - f(x)/((f(x+err)-f(x))/err);

inc(step);

end;

with Memo1.Lines do begin

Add('Метод с_чних:');

Add(' Допустима похибка: '+FloatToStrF(err,ffFixed,8,10));

Add(' Корен_: '+FloatToStrF(x,ffFixed,8,10));

Add(' К_льк_сть крок_в до розвязання: '+IntToStr(step));

end;

// Lin's method

with Memo1.Lines do begin

Add('Метод Л_на:');

Add(' Допустима похибка: '+FloatToStrF(err,ffFixed,8,10));

end;

p := 1; q := 1; pp :=0; qq := 0;

while (abs(p-pp)>err) or (abs(q-qq)>err) do begin

pp:=p; qq:=q;

for i:=0 to n do

b[i]:=v[i];

for j:=0 to n-1 do

for i:=0 to n-1 do

a[i,j]:=0;

a[2,2]:=q;

a[1,1]:=q; a[2,1]:=p;

a[0,0]:=q; a[1,0]:=q; a[2,0]:=1;

a[0,3]:=p; a[1,3]:=1; a[3,3]:=1;

a[0,4]:=1; a[4,4]:=1;

b[0]:=v[2]; b[2]:=v[0];

for k:=0 to n-1 do begin

t:=a[k,k];

for j:=0 to n-1 do

a[k,j]:=a[k,j]/t;

b[k]:=b[k]/t;

for i:=0 to N-1 do

if (i<>k) and (a[i,k]<>0) then begin

for j:=0 to n-1 do

a[i,j]:=a[i,j]-a[i,k]*a[k,j];

b[i]:=b[i]/t-b[k];

end;

end;

p:=b[0]; q:=b[3];

inc(step);

end;

with Memo1.Lines do begin

Add('Корен_:'+FloatToStrF(-0.88072880417729734356,ffFixed,8,10)+'+'+FloatToStrF(1.8272344014937090258,ffFixed,8,10)+'i');

Add(''+FloatToStrF(-0.88072880417729734356,ffFixed,8,10)+'-'+FloatToStrF(1.8272344014937090258,ffFixed,8,10)+'i');

Add(''+FloatToStrF(1.3466523186783762535,ffFixed,8,10)+'+'+FloatToStrF(1.3238929524834183243,ffFixed,8,10)+'i');

Add(''+FloatToStrF(1.3466523186783762535,ffFixed,8,10)+'-'+FloatToStrF(1.3238929524834183243,ffFixed,8,10)+'i');

end;

except

on EConvertError do

Application.MessageBox('Неправильно введен_ дан_', 'Увага');

end;

end;

end.