Числа с фиксированной точкой

4. Числа с фиксированной точкой

Такие числа могут быть как целыми, так и дробными. Точка мысленно фиксируется рядом с любым разрядом. Если она располагается справа от младшего бита, то число целое, если слева от старшего - число дробное. Далее будут рассматриваться только целые числа с фиксированной точкой, для нецелых чисел чаще применяется показательная форма, о которой пойдет речь дальше.

Естественным представлением целого неотрицательного числа является двоичная система счисления. Кодирование отрицательных чисел производится тремя наиболее употребительными способами, в каждом из которых крайний левый бит - знаковый. Отрицательному числу соответствует единичный бит, а положительному - нулевой. Каждый способ оценивается по скорости и затратам на выполнение сложения и изменения знака числа, т.к. вычитание есть сложение с измененным знаком одного операнда.

  4.1 Прямой код

Изменение знака производится просто, путем инверсии бита знака. Пусть 00001001 = 9, тогда 10001001 = -9. Если при сложении двух чисел в этом коде знаки совпадают, то трудностей нет. Если знаки различаются необходимо найти наибольшее число, вычесть из него меньшее, а результату присвоить знак наибольшего слагаемого.

  4.2 Обратный код, инверсный или дополнительный "до 1"

Изменение знака производится просто - инверсией всех бит: 00001001 = 9, а 11110110 = -9. Сложение также выполняется просто, т.к. знаковые биты можно складывать. При переносе единицы из левого (старшего) бита, она должна складываться с правым (младшим). Например: 7 + (-5) = 2.

00000111 = 7

11111010 =-5 (инверсия 00000101 = 5)

1 00000001

1 00000010 = 2

Сложение в обратном коде происходит быстрее, т.к. не требуется принятие решения, как в предыдущем случае. Однако суммирование бита переноса требует дополнительных действий. Другим недостатком этого кода является представление нуля двумя способами, т.к. инверсия 0...00 равна 1. ..11 и сумма двух разных по знаку, но равных по значению чисел дает 1...11.Например: (00001001 = 9) + (11110110 = -9) = 11111111. Кстати, из этого примера понятно почему код называется дополнительным "до 1".

  4.3 Дополнительный или дополнительный "до 2" код

Число с противоположным знаком находится инверсией исходного и добавлением к результату единицы. Например, найти код числа -9.

00001001 = 9 11110111 =-9

11110110 - инверсия 00001000 - инверсия

1 1

11110111 =-9 00001001 = 9

Проблемы двух нулей нет. +0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос из старшего бита не учитывается).Сложение производится по обычным для неотрицательных чисел правилам.

00001001 = 9

11110111 =-9

1 00000000

Из этого примера видно, что в каждом разряде двух равных по модулю чисел складываются две единицы, что и определило название способа. Этот метод применяется наиболее часто, и когда говорят о дополнительном коде, то имеется в виду дополнительный "до 2-х" код.

5. Схема алгоритма

6. Программная реализация алгоритма Общие сведения

Программа написана на языке Turbo Pascal 7.0 . Минимальные требования к конфигурации системы: процессор 80386 и выше. Исполняемый файл MS-DOS "v1_13.exe".

Файл с исходными данными должен находиться в том же каталоге, что и "v1-13.exe", и носить название "in.txt". Файл результатов работы - "out.txt".

Данные должны быть целыми числами(возможно со знаком) в диапазоне от –128..+127, т.к. для реализации задачи была выбрана 8 разрядная двоичная сетка.

Описание использованных функций и процедур

В данной работе для перевода из одной системы в другую используется несколько функций:

v  DecToBase – выполняет перевод из десятичной в 2-16 системы счисления;

v  BaseToInt – обратный перевод из Base-системы счисления в десятичную СС;

DecToBase

Данная функция является программным осуществлеием алгоритма преобразования числа из десятичной системы счисления в любую другую, описанного выше.

Удобство функции заключается в том, что она чувствительнак знаку числа и по умолчанию при переводе в двоичную систему счисления использует дополнительный "до 1" код, что избавляет нас от написания дополнительной функции перевода.

BaseToInt

Данная функция реализует алгоритм преобразования числа Base- системы счисления в десятичную по следующей формуле:

x = a_nPⁿ + a_n-1P^n-1 + ... + a₁P¹ + a₀P⁰ + a_-1P^-1 + ... + a_-mP^-m

p-основание СС; Х – десятичное представление числа.

Функция определяет знак числа за счет учета инверсии: т.к. используем 8 разрядную двоичную сетку и числа со знаком, то имеет 128 отрицательных и 127 положительных значений и ноль (всего 256), то есть отрицательная величина лежит в диапазоне беззнаковых значений 128..256. А выражение (256-<x>), где <x> - беззнаковая величина после преобразования, есть модуль отрицательного числа.

Функции сложения и вычитания Сложение. Функция BinPlus

Функция бинарного сложения работает по следующему алгоритму.

Вычитание. Функция BinMinus.

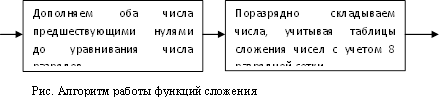
Принцип работа данной функции основан на тождестве a-b=a+(-b).

Библиографический список

1.         Turbo Pascal 7.0.(том 1)/ Фаронов., Питер. Прес.,2000г.

2.         "Введение в информатику. Лабораторные работы." / Авт.-сост. А.П. Шестаков; Перм. ун-т. — Пермь, 1999. (Ч. I — 56 с.)

3.         Основы информатики/ Савельев А.Я. , МГТУ им. Баумана.

 

Приложение

Исходный текст программы

{для реализации данной программы взята 8 разрядная двоичная сетка}

{следовательно диапазон значений должен быть с пределах от -127..127}

Program CourceProject_v1_13;

uses Crt;

const

Group=’246’;

Name=’’; {Фамилия И.О. студента}

PrepName=’’; {Фамилия И.О. преподавателя}

InFileName=’in.txt’;

OutFileName=’Out.txt’;

function StrToVal(Ch:Char):byte;

var value,code:integer;

begin

val(Ch,value,code);

StrToVal:=value;

end;

function ValToStr(val:byte):Char;

var ch:string;

begin

Str(val,ch);

ValToStr:=ch[1];

end;

{Перевод из десятичной в 2-16 систему счисления}

function DecToBase(Decimal: LongInt; const Base: Byte): String;

const

Symbols: String[16] = ’0123456789ABCDEF’;

var

scratch: String;

remainder: Byte;

temp:byte;

begin

{инверсия числа если знак его "-"}

if Decimal<0 then Decimal:=(256-abs(Decimal));

scratch := ’’;

repeat

remainder := Decimal mod Base; {остаток от деления }

scratch := Symbols[remainder + 1] + scratch;

{символ соотв. остатку}

Decimal := Decimal div Base;

{собс-но деление}

until ( Decimal = 0 );

DecToBase := scratch;

end;

{Перевод из 2-16 в 10ю систему счисления}

function BaseToInt(Value: String;Base:byte): LongInt;

var

i,m,Result,c: Integer;

begin

 Result:=0;

m:=1;

for i:=Length(Value) downto 1 do

begin

if i=(Length(Value)-1) then m:=base;

case Value[i] of

’A’:c:=10;

’B’:c:=11;

’C’:c:=12;

’D’:c:=13;

’E’:c:=14;

’F’:c:=15;

else

c:=StrToval(Value[i])

end;{case}

result:=result+m*c;

m:=m*base;

end;

{находим знак числа}

if result>127 then result:=result-256;

 BaseToInt:=Result;

end;

{подготовка чисел к вып. арифм. действий}

procedure Prepare(var Value1,Value2:string;var Len:byte);

var

i,j,m:byte;

temp:string;

begin

{выбираем самое длинное число}

i:=length(Value1);

j:=length(Value2);

len:=i;

if i>j then

begin

len:=i;

{дополняем меньшую строку нулями до равного колва символов}

for m:=1 to (i-j) do insert(’0’,Value2,1);

end

else {j>i}

begin

len:=j;

{дополняем меньшую строку нулями до равного колва символов}

for m:=1 to (j-i) do insert(’0’,Value1,1);

end;

end;

{двоичное сложение}

function BinPlus(BIN1,BIN2:string):String;

var summ:string[50];

temp,pl_razryad:integer;

k,m:byte;

begin

summ:=’’;

pl_razryad:=0;

{подготовка к сложению чисел}

Prepare(BIN1,BIN2,k);

for m:=k downto 1 do

begin

{Складываем соотвествующие разряды + "что на ум пошло"}

temp:=StrToVal(BIN1[m])+StrToVal(BIN2[m])+pl_razryad;

{обнуляем то что на "ум пошло"}

pl_razryad:=0;

If temp>7 then

begin

inc(pl_razryad);

temp:=temp-2;

end;

{избавляемся от переполнения разрядной сетки}

if length(summ)<=8 then insert(ValToStr(temp),summ,1);

end;

{еслои после сложения двух числел что-то осталось "в уме"

добавляем еще один разряд}

if pl_razryad<>0 then insert(valtostr(pl_razryad),summ,1);

BINPlus:=summ;

end;

{двоичное вычитание}

function BinMinus(BIN1,BIN2:string):String;

var inverseBIN2:string[8];

begin

{т.к. вычитание есть сложение первой величины и

второй величины взятой с инверсией, то можно

делать так}

{инверсия величины BIN2}

inverseBIN2:=DecToBase(-BaseToInt(BIN2,2),2);

{сложение BIN1 и инверсной Bin2}

BinMinus:=BinPlus(BIN1,inverseBIN2);

end;

{Вывод лого}

procedure Logo;

var

i:byte;

begin

ClrScr;

{отрисуем рамку}

GotoXY(1,1);

TextColor(3);

for i:=1 to 80 do Write(’*’);

for i:=1 to 22 do Write(’*’,’*’:79);

for i:=1 to 80 do Write(’*’);

{Конец рамки}

{Выводим текст}

GotoXY(25,10);

Write(’К У Р С О В А Я Р А Б О Т А’);

GotoXY(27,12);

Write(’по дисциплине "ИНФОРМАТИКА"’);

GotoXY(65,17);

Write(’Выполнила:’);

GotoXY(65,18);

Write(’ст.гр.’,Group);

GotoXY(65,19);

Write(Name);

GotoXY(65,20);

Write(’Проверил:’);

GotoXY(65,21);

Write(PrepName);

end;

var

FileIn:Text; {Файл исходных данных }

FileOut:Text; {Файл результатов выполнения программы}

Int1,Int2:integer; {исх. данные из файла }

Hex1,BIN1:String; {Число в различных системах счисления}

Hex2,BIN2:String; {Число в различных системах счисления}

ResMin,ResPlus:string; {Результат выполнения ар. действий}

begin {тело}

Logo; {Показываем лого нашей работы }

GotoXY(23,25);

WriteLn(’Для продолжения нажмите любую клавишу...’);

repeat

until KeyPressed;

{Читаем из файла необходимые данные}

Assign(FileIn,InFileName);Reset(FileIn);

ReadLn(FileIn,Int1); {читаем первое число }

ReadLn(FileIn,Int2); {читаем второе число }

Close(FileIn);

{Создаем условия для работы программы}

HEX1:=DecToBase(int1,16); {Переводим первое число в HEX}

HEX2:=DecToBase(int2,16); {Переводим второе число в HEX}

BIN1:=DecToBase(BaseToInt(HEX1,16),2);{перевод из 16 в двоичную с-му}

BIN2:=DecToBase(BaseToInt(HEX2,16),2);{перевод из 16 в двоичную с-му}

ResPlus:=BINPlus(BIN1,BIN2); {Выполняем сложение 2й с-ме }

{приводим р-т сложения к заданному виду, т.е. в 16ю с-му}

ResPlus:=DecToBase(BaseToInt(ResPlus,2),16);

ResMin:=BINMinus(BIN1,BIN2); {Выполняем вычитание 2й с-ме }

{приводим р-т вычитания к заданному виду, т.е. в 16ю с-му}

ResMin:=DecToBase(BaseToInt(ResMin,2),16);

Assign(FileOut,OutFileName);Rewrite(FileOut);

WriteLn(FileOut,’Исходные данные:’);

WriteLn(FileOut,’ Число 1 :’,BaseToInt(HEX1,16));

WriteLn(FileOut,’ Число 2 :’,BaseToInt(HEX2,16));

WriteLn(FileOut);

WriteLn(FileOut,’Pезультат выполнения программы:’);

WriteLn(FileOut,’ Сложение :’,BaseToInt(ResPlus,16));

WriteLn(FileOut,’ Вычитание:’,BaseToInt(ResMin,16));

Cloose(FileOut);

end.

Файл исходных данных (in.txt)

25

-30

Файл результата работы программы (out.txt)

Исходные данные:

Число 1 : 25

Число 2 : -30

Результат выполнения программы:

Сложение :-5

Вычитание:55