Навигация
Требования к остаткам
2.2 Требования к остаткам
При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей ![]() . В модели
. В модели
![]()
случайная составляющая ![]() представляет собой ненаблюдаемую величину. В задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений
представляет собой ненаблюдаемую величину. В задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений ![]() , т. е. остаточных величин.
, т. е. остаточных величин.
Проверка статистической достоверности коэффициентов регрессии и корреляции осуществляется с помощью t-критерия Стьюдента, F-критерия Фишера и Z-преобразования (для коэффициентов корреляции). При использовании этих критериев делаются предположения относительно поведения остатков ![]() - остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.
- остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.
Оценки параметров регрессии должны быть несмещенными, состоятельными и эффективными. Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.
Исследования остатков ![]() предполагают проверку наличия следующих пяти предпосылок МНК:
предполагают проверку наличия следующих пяти предпосылок МНК:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не зависящая от ![]() ;
;
3) гомоскедастичность - дисперсия каждого отклонения ![]() одинакова для всех значений х;
одинакова для всех значений х;
4) отсутствие автокорреляции остатков. Значения остатков ![]() распределены независимо друг от друга;
распределены независимо друг от друга;
5) остатки подчиняются нормальному распределению.
Если распределение случайных остатков ![]() не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Прежде всего проверяется случайный xapактер остатков ![]() - первая предпосылка МНК.
- первая предпосылка МНК.
С этой целью стоится график зависимости остатков ![]() от теоретических значений результативного признака (рис. 3.2).
от теоретических значений результативного признака (рис. 3.2).
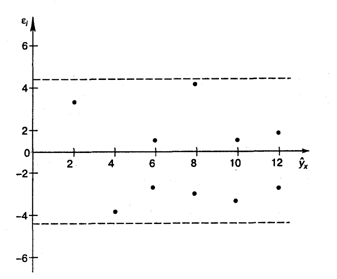
Рис.3.2. Зависимость случайных остатков ![]() от теоретических значений
от теоретических значений ![]()
Если на графике получена горизонтальная полоса, то остатки ![]() представляют собой случайные величины и MНK оправдан, теоретические значения
представляют собой случайные величины и MНK оправдан, теоретические значения ![]() хорошо аппроксимирует фактические значения у.
хорошо аппроксимирует фактические значения у.
Возможны следующие случаи: если ![]() зависит от
зависит от ![]() , то:
, то:
а) остатки ![]() не случайны;
не случайны;
б) остатки ![]() не имеют постоянной дисперсии;
не имеют постоянной дисперсии;
в) остатки ![]() носят систематический характер.
носят систематический характер.
В случаях а), б), в) необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки ![]() не будут случайными величинами.
не будут случайными величинами.
Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что![]() . Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
Вместе с тем несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных остатков и величин х, что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью строится график зависимости случайных остатков ![]() от факторов, включенных в регрессию
от факторов, включенных в регрессию ![]() (рис. 3.4).
(рис. 3.4).
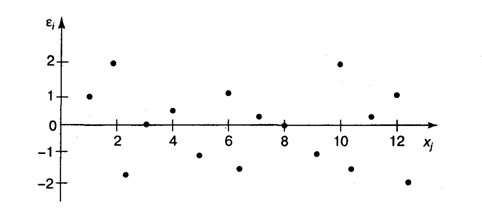
Рис. 3.4. Зависимость случайных остатков от величины фактора ![]()
Если остатки на графике расположены в виде горизонтальной полосы (рис. 3.4), то они независимы от значений ![]() . Если же график показывает наличие зависимости
. Если же график показывает наличие зависимости ![]() и
и ![]() , то модель неадекватна.
, то модель неадекватна.
Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F.[1] Всегда, прежде чем сделать окончательные выводы, стоит рассмотреть распределения представляющих интерес переменных. Можно построить гистограммы или нормальные вероятностные графики остатков для визуального анализа их распределения.[электрон-уч]
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора ![]() остатки
остатки ![]() имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.5).
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.5).
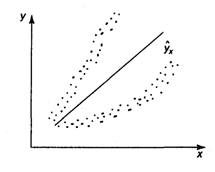
Рис. 3.5. Пример гетероскедастичности: дисперсия остатков растет по мере увеличения х;
Используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо- и гетероскедастичность (рис. 3.6, 3.7).
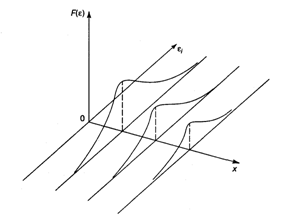
Рис. 3.6. Гомоскедастичность остатков
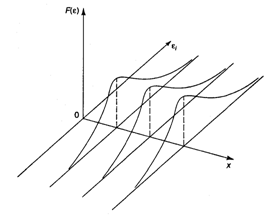
Рис. 3.7. Гетероскедастичность остатков
Рис. 3.6 показывает, что для каждого значения ![]() распределения остатков
распределения остатков ![]() одинаковы в отличие от рис. 3.7, где диапазон варьирования остатков меняется с переходом от одного значения
одинаковы в отличие от рис. 3.7, где диапазон варьирования остатков меняется с переходом от одного значения ![]() другому. Соответственно на рис. 3.7 демонстрируется неодинаковая дисперсия при разных значениях
другому. Соответственно на рис. 3.7 демонстрируется неодинаковая дисперсия при разных значениях ![]() .
.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков ![]() от теоретических значений результативного признака
от теоретических значений результативного признака ![]() . Так, для рис 3.5 зависимость остатков от
. Так, для рис 3.5 зависимость остатков от ![]() представлена на рис. 3.8.
представлена на рис. 3.8.
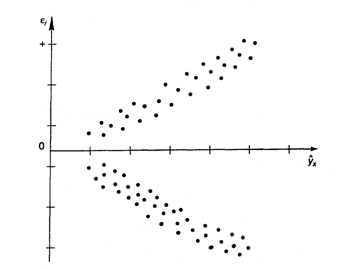
Рис. 3.8. Гетероскедастичность: большая дисперсия ![]() для больших значений
для больших значений ![]()
При построении рефессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК - отсутствие автокорреляции остатков, т. е. значения остатков ![]() , распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. [1]
, распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. [1]
Одним из основных предполагаемых свойств отклонений ![]() от регрессионной модели является их статистическая независимость между собой. Поскольку значени
от регрессионной модели является их статистическая независимость между собой. Поскольку значени ![]() остаются неизвестными, то проверяется статистическая независимость их аналогов — отклонения
остаются неизвестными, то проверяется статистическая независимость их аналогов — отклонения ![]() (наблюдаемые значения ошибок). При этом устанавливается некоррелированность сдвинутыми на период величинами
(наблюдаемые значения ошибок). При этом устанавливается некоррелированность сдвинутыми на период величинами ![]() . Для этих величин можно рассчитать коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции между
. Для этих величин можно рассчитать коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции между ![]() и
и ![]() ):
):
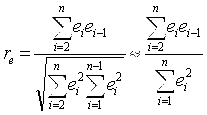
На практике в качестве теста используют тесно связанную с коэффициентом автокорреляции ![]() статистику Дарбина — Уотсона. Тест Дарбина — Уотсона (DW) на наличие или отсутствие автокорреляции ошибок рассчитывается по формуле:
статистику Дарбина — Уотсона. Тест Дарбина — Уотсона (DW) на наличие или отсутствие автокорреляции ошибок рассчитывается по формуле:

Нулевая гипотеза состоит в отсутствии автокорреляции. Статистику Дарбина-Уотсона можно выразить через коэффициент автокорреляции:
![]() [2]
[2]
Содержательный смысл статистики Дарбина-Уотсона заключается в следующем: если между ![]() и
и ![]() имеется достаточно высокая положительная корреляция, то
имеется достаточно высокая положительная корреляция, то ![]() и
и ![]() близки друг другу и величина статистики DW мала. Это согласуется с последним выражением: если коэффициент
близки друг другу и величина статистики DW мала. Это согласуется с последним выражением: если коэффициент ![]() близок к единице, то величина DW близка к нулю. Отсутствие корреляции означает, что DW близка к 2. [3]
близок к единице, то величина DW близка к нулю. Отсутствие корреляции означает, что DW близка к 2. [3]
Если бы распределение статистики DW было известно, то для проверки гипотезы ![]() против альтернативы
против альтернативы ![]() можно было бы для заданного уровня значимости (например, для 5%-уровня) найти такое критическое значение
можно было бы для заданного уровня значимости (например, для 5%-уровня) найти такое критическое значение ![]() , что если
, что если![]() , то гипотеза Но не отвергается, в противном случае она отвергается в пользу Н1. Проблема, однако, состоит в том, что распределение DW зависит не только от числа наблюдений п и количества регрессоров к, но и от всей матрицы X, и, значит, практическое применение этой процедуры невозможно. Тем не менее, Дарбин и Уотсон доказали, что существуют две границы, обычно обозначаемые
, то гипотеза Но не отвергается, в противном случае она отвергается в пользу Н1. Проблема, однако, состоит в том, что распределение DW зависит не только от числа наблюдений п и количества регрессоров к, но и от всей матрицы X, и, значит, практическое применение этой процедуры невозможно. Тем не менее, Дарбин и Уотсон доказали, что существуют две границы, обычно обозначаемые ![]() и
и ![]() ,
,![]() (и = upper - верхняя, l = low - нижняя), которые зависят лишь от n, к и уровня значимости (а следовательно, могут быть затабулированы) и обладают следующим свойством: если
(и = upper - верхняя, l = low - нижняя), которые зависят лишь от n, к и уровня значимости (а следовательно, могут быть затабулированы) и обладают следующим свойством: если![]() , то
, то ![]() и, значит, гипотеза H0 не отвергается, а если
и, значит, гипотеза H0 не отвергается, а если ![]() то
то![]() , и гипотеза Ноотвергается в пользу H1. В случае
, и гипотеза Ноотвергается в пользу H1. В случае ![]() ситуация неопределенна, т. е. нельзя высказаться в пользу той или иной гипотезы. Если альтернативной является гипотеза об отрицательной корреляции
ситуация неопределенна, т. е. нельзя высказаться в пользу той или иной гипотезы. Если альтернативной является гипотеза об отрицательной корреляции![]() , то соответствующими верхними и нижними границами будут 4-dl и 4-du. Целесообразно представить эти результаты в виде следующей таблицы.
, то соответствующими верхними и нижними границами будут 4-dl и 4-du. Целесообразно представить эти результаты в виде следующей таблицы.
Таблица 6.3.
Значение статистики DW
| Значение статистики DW | Вывод |
| 4 -dl< DW < 4 | Гипотеза Но отвергается, есть отрицательная корреляция |
| 4 - du < DW < 4 - dl | Неопределенность |
| du < DW < 4 - du | Гипотеза Но не отвергается |
| dl < DW < du | Неопределенность |
| 0 < DW < dl | Гипотеза Но отвергается, есть положительная корреляция |
Наличие зоны неопределенности, представляет определенные трудности при использовании теста Дарбина-Уотсона. [3]
Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы, преобразовывать исходные данные для того, чтобы получить оценки коэффициентов регрессии, которые обладают свойством несмещенности, имеют меньшее значение дисперсии остатков и обеспечивают в связи с этим более эффективную статистическую проверку значимости параметров регрессии. [1]
0 комментариев