Вычисление значения интеграла функции

1. Вычисление значения интеграла функции,

заданной графически

 

1.1. Задания и постановка задачи.

Задание (вариант №15):

Составить программу на языке Turbo Pascal 7.0 вычисления значения интеграла на интервале [a, b] для функции, заданной графически. Значение интеграла вычислить приближённо по итерационной формуле левых прямоугольников:

 b

I = ò f (x)dx @ In = h(f1 + f2 +…+ fn-1),

 a

где h=(b-a)/n – величина шага между двумя соседними точками разбиения интервала интегрирования; fi = f(xi) – значение функции в точке xi = a + h(i –1); i = 1, 2, …, n.

Вычисления закончить при выполнении условия |In – I2n| < e, где e>0 – достаточно малое значение, задаваемое пользователем (точность вычислений). Здесь In, I2n – значения интеграла, вычисленные по данной формуле при количестве разбиения на n и 2n соответственно.

Численные значения всех величин, участвующих в вычислениях, считать параметрами программы и определить их путём ввода.

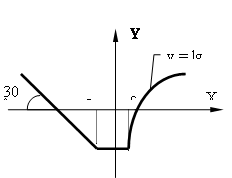График функции:

Пояснение к заданию:

Анализируя график функции можно сделать вывод, что для аналитического задания уравнения функции следует ее рассматривать на различных интервалах:

 x <= -c Þ y = kx + b

 -c < x < =c Þ y = Ln(c)

 c < x Þ y = lg(x),

 

где kx + b =, lg x= (ln(x))/(ln(10));

x – аргумент функции; y – её значение; c – параметр функции (c>0), вводимые пользователем с клавиатуры.

1.2 Математическая формулировка задачи.

Решение многих задач (например, определение пути при неравномерном движении, работы переменной силы, расходов воды в реках и каналах, площади поперечного сечения судна) находится с помощью определённого интеграла. Иногда для вычисления определённого интеграла от непрерывной на отрезке [a; b] функции f(x) можно просто воспользоваться формулой Ньютона-Лейбница:

 b

S = ò f(x) dx = F(b) – F(a),

 a

где F(x) – первообразная для функции f(x) [F¢(x)=f(x)].

Однако воспользоваться формулой Ньютона-Лейбница в большинстве ситуаций не представляется возможным.

В этом случае используются приближённые методы для вычисления определённого интеграла. Все они основаны на том, что геометрически интеграл функции f(x) в пределах от a до b представляет собой площадь криволинейной трапеции, ограниченной графиком этой функции, осью Ox и прямыми x = a, x = b. Рассмотрим один из этих методов.

1.3 Численный метод решения.

Пусть требуется приближённо вычислить площадь фигуры, ограниченной графиком функции f(x) и прямыми x = a, x = b, y = 0.

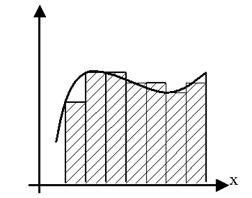Идея алгоритма вычисления площади криволинейной трапеции состоит в следующем:

 Разобьем отрезок [a; b] на n равных отрезков точками a = x0 < x1 < x2 <…< xn-1 < xn = b и на каждом из полученных отрезков построим прямоугольник, одной стороной которого будет отрезок [xi, xi+1 ], а другой – отрезок, длина которого равна f(xi). Этот случай показан на рисунке 2.

Площадь криволинейной трапеции можно приближённо считать равной сумме площадей заштрихованных прямоугольников.

Ясно, что если увеличивать число отрезков [ xi, xi+1 ], т.е. отрезок

 [a; b] разбивать на большее число равных отрезков, то сумма их площадей всё с большей точностью будет совпадать с площадью криволинейной трапеции. Значит, точность вычисления площади криволинейной трапеции определяется величиной числа n.

Площадь каждого прямоугольника можно вычислить так. Одна из сторон прямоугольника, построенного на отрезке [ xi, xi+1 ], равна h = (b - a) / n, а вторая – f(xi). Поэтому площадь «левого» прямоугольника равняется s = h * f(xi) = (b - a) / n * f(xi). Тогда площадь криволинейной трапеции равна сумме площадей всех прямоугольников:

S = (b - a)/n * f(x0) + (b - a)/n * f(x1) + … + (b - a)/n * f(xn-1) = (b - a)/n * ( f(x0) + f(x1) +…+ f(xn-1) ).

Таким образом, мы нашли интеграл функции f(x) на отрезке [a; b] при числе разбиений отрезка n. Очевидно, что чем больше n, тем больше точность вычисления значения интеграла; однако, при этом время, затрачиваемое на решение задачи, также прямо пропорционально числу n. Отсюда возникает вопрос: как правильно выбрать значение числа n, чтобы за наименьшее время найти значение искомого интеграла с предельно допустимой точностью?

Пусть мы знаем, что при разбиении отрезка интегрирования на n частей интеграл функции на данном интервале равен Integral1. Тогда мы можем также найти значение интеграла при числе разбиений отрезка, равном 2n, и это значение будет равняться некоторому числу Integral2. Очевидно, что оценкой точности вычислений будет являться величина абсолютной погрешности |Integral1 - Integral2|. Но в таком случае, именно величина абсолютной погрешности и есть тот критерий, который показывает, следует ли дальше продолжать вычисления или найденное значение интеграла уже удовлетворяет предельно допустимому уровню погрешности в поставленной задаче.

Тогда алгоритм решения задачи заключается в следующем:

Сначала вычисляется значение интеграла при n разбиений отрезка интегрирования (Integral1). Затем число разбиений n увеличивается в 2 раза и вычисляется значение интеграла при новом числе разбиений (Integral2). После этого проверяется условие завершения работы (|Integral1 - Integral2|<e) и, если работу следует продолжать, то текущее значение Integral2 присваивается значению Integral1, число разбиений n увеличивается в 2 раза, а значение Integral2 вычисляется заново и так далее, пока не будет выполнено условие |Integral1 - Integral2|<e.

Теперь нерешённым остался только вопрос о выборе начального значения числа n. Очевидно, что этот вопрос нельзя разрешить однозначно и одинаково для всех видов функций. Это станет очевидно, если рассмотреть следующую ситуацию: пусть требуется найти определённый интеграл некоторой функции на отрезке, где она принимает некоторое одинаковое значение не менее 2-х раз, и при этом её интеграл не равен произведению этого значения на длину отрезка интегрирования. При некорректном выборе исходного значения n может получиться так, что при разбиении отрезка интегрирования на n и 2n в рассмотрение будут приняты только те точки, значения функции в которых совпадают. Но тогда вычисление интеграла закончатся, т.к. разница между найденными значениями (Integral1 - Integral2) будет равна нулю и, следовательно, явно меньше любой погрешности, значение которой всегда положительно. Но это недопустимо, т.к. реальное значение искомого интеграла может быть далеко от найденного. Поэтому, при рассмотрении каждой новой функции следует производить тщательный анализ и исключение подобных ситуаций. Таким образом, вопрос о выборе начального значения числа разбиений отрезка остается открытым.

Так как рассматриваемая в данной задаче функция не представляет особой сложности, то в предложенном далее алгоритме решения задачи начальное значение числа n будет взято равным единице.