Навигация
Класифікація моделей і методів візуалізації
2.1.1 Класифікація моделей і методів візуалізації
На даний час відоме досить велике кількість різних методів подання тривимірних об'єктів і пов'язаних з ними методів візуалізації, у тому числі багатомасштабних. Всі подання можна розділити на кілька класів, що володіють характерними властивостями:
Поверхневі / об'ємні.
Зв'язані / дискретні.
Явні / параметричні.
Поверхневі моделі описують тільки поверхню об’єкта в тривимірному просторі. На противагу їм, об'ємні (воксельні) структури дозволяють задавати моделі, як частину тривимірного простору, розбитого деяким чином на осередки, які вважаються заповненими, якщо вони містять частину об’єкта, і порожніми – у противному випадку.
Зв'язані моделі явно або неявно містять інформацію про безперервні ділянки поверхонь моделей, тоді як дискретні подання описують тільки наближення поверхні об’єкта.
Явне завдання моделей припускає, що опис моделі об’єкта в даному поданні доступно в явній формі, а параметричне – що для його одержання необхідно додатково обчислювати деяку функцію, яка залежить від параметру.
Методи візуалізації можна умовно розділити на проекційні методи й методи трасування променів.
Проекційні методи - це методи, у яких синтез зображення виконується за допомогою афінних перетворень і перетворень проекції. Тривимірна сцена як набір примітивів візуалізації (звичайно, багатокутників, точок, ліній тощо) трансформується у двомірний масив, що і відображається на екрані монітора.
Методи трасування променів працюють на рівні пікселів вихідного зображення, розраховуючи їхні кольори на основі даних про геометрію сцени і положення віртуальної камери.
Сьогодні інтерактивну швидкість синтезу зображень надають тільки проекційні методи, часто за підтримкою апаратного забезпечення. Надалі в роботі розглядаються тільки такі методи, які в свою чергу накладають деякі обмеження на можливі подання об'єктів. Характерною рисою поставленого завдання є робота з реальними даним, тобто даними, введеними в комп'ютер за допомогою пристроїв дистанційного сканування. Такі дані, в більшості випадків, дискретні й задані явно, звичайно у вигляді набору точок або набору карт глибини. Крім того, за винятком томографів (цей випадок у роботі не розглядається), що одержують внутрішню структуру об’єкта, всі сканери працюють тільки з поверхнею об’єкта. Таким чином, подання повинне гарно описувати явно задані дискретні поверхні.
Проведемо аналіз різних подань із метою виявлення придатності їхнього використання для рішення поставленого завдання. У тексті не розглядаються різні параметричні й процедурні подання тому, що їх особливості (складність обчислень, відсутність апаратної підтримки) роблять складним використання цих подань для моделювання реальних об'єктів.
2.1.2 Полігональні сітки
Полігональні сітки є на даний момент найпоширенішим поданням, для якого створене велика кількість програмного забезпечення, що дозволяє редагувати, передавати по мережі й відображати моделі з використанням апаратної підтримки.
Характерною рисою полігональних сіток є підтримка зв’язності моделі. У силу цього полігональні подання добре пристосовані для опису великої кількості синтетичних поверхонь.
Однак, відскановані дані, споконвічно не містять інформації про зв’язність й безперервність поверхонь, а являють собою набір близько розташованих часток (sample). Такі обмеження випливають із пристрою скануючого механізму, що має дискретний крок кінцевого розширення.
Отже, для використання полігональних моделей зв’язність повинна бути введена штучно на етапі препроцесуванні. Таким чином, полігональні моделі не призначені для прямої роботи з від сканованими даними, тому що вимагають відновлення поверхні, що в загальному випадку є нетривіальним завданням і сильно залежить від класу оброблюваних об'єктів. При цьому відновлена поверхня не обов'язково буде використовуватися на етапі візуалізації (наприклад, якщо модель такої складності, що проекція трикутника на екран при типовій проекції перегляду близька по площі з одним пікселем).
З іншого боку, створена велика кількість методів, що дозволяють досить ефективно перетворювати дискретні від скановані дані в полігональні сітки. Більше того, сучасне устаткування високого класу дозволяє виконувати перетворення в сітку апаратно [1].
Набагато складніше ситуація з поданням великих обсягів даних і підтримкою різних рівнів деталізації. Структура полігональних сіток лінійна й вони не забезпечують «природної» підтримки багатомасштабності. Тому робота з великими сітками ускладнена і потребує різних, найчастіше обчислювально складних методів спрощення. Було створено безліч алгоритмів для створення багатомасштабних подань на основі сіток, що мають безпосереднє відношення до поставленого завдання.
Практично всі технології спрощення сіток використовують деякі варіації або комбінації наступних механізмів: семплюваня (sampling), проріджування (decimation), адаптивної розбивки (adaptive subdivision) і злиття вершин (vertex merging) [2].
Алгоритми семплюваня спрощують первісну геометрію моделі, використовуючи або підмножину вихідних точок, або перетинання вокселів з моделлю на тривимірній сітці. Такі алгоритми найкраще працюють на гладких поверхнях без гострих кутів.
Алгоритми, що використовують адаптивну розбивку, знаходять просту базову (base) сітку, що потім рекурсивно розбивається для апроксимації первісної моделі. Такий підхід працює добре, коли знайти базову модель відносно просто. Наприклад, базова модель для ділянки ландшафту звичайно прямокутник. Для досягнення гарних результатів на довільних моделях потрібне створення базової моделі, що відбиває важливі властивості вихідної, що може бути нетривіально.
Проріджуючи алгоритм, ітеративно видаляє вершини або грані з полігональної сітки, роблячи тріангуляцію після кожного кроку. Більшість із них використають тільки локальні зміни, що дозволяє виконувати спрощення досить швидко (рис. 2.1).
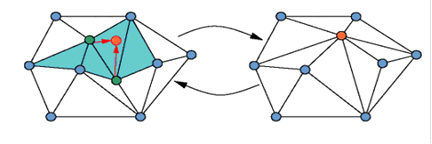
Рис.2.1. Об’єднання ребер (процес тріангуляції)
Схеми зі злиттям вершин працюють за допомогою об’єднання двох або більше вершин деталізованої моделі в одну, котра у свою чергу може бути сполучена з іншими вершинами. Злиття вершин трикутника знищує його, зменшуючи загальне число трикутників моделі. Звичайно алгоритми використовують складні методи визначення, які вершини потрібно об’єднати разом і у якому порядку. Методи, що використовують злиття ребер (edge collapse), завжди зливають вершини, що розділяють одну грань. Такі методи зберігають локальну топологію і, крім того, при деяких умовах можуть працювати в реальному часі.
Складність обчислень у цих методах висока і їхнє використання не завжди виправдане при роботі з дискретними даними, оскільки складність з'являється насамперед через необхідність підтримувати зв’язаність моделі. Іншою причиною високої складності методів є лінійна структура сітки, яку необхідно відновлювати для візуалізації за допомогою графічних API.
Переваги даного алгоритму: розповсюджене представлення; апаратна підтримка.
Недоліки алгоритму: неефективні для роботи з дискретними даними через штучну підтримку зв’язності, складного препроцесінга; неефективні для більших моделей через труднощі з організацією багатомасштабності.
Похожие работы
... або напрямоку камери, то параметр повинен бути GL_PROJECTІON. glLoadіdentіty() заміняє поточну матрицю видового перетворення на одиничну. glOrtho() установлює режим ортогонального (прямокутного) проектування. Це значить, що зображення буде рисуватися як в ізометрії. 6 параметрів типу GLdouble (або просто double): left, rіght, bottom, top, near, far визначають координати відповідно лівої, право ...
... . Від цього залежатиме, яким чином у подальшому слід будувати процес навчання в початкових класах загальноосвітньої школи. Розділ 2. Формування у молодших школярів навичок виконання зображень птахів і тварин 2.1 Методика виконання зображень птахів і тварин у початкових класах Тваринний світ дуже цікавий і різноманітний за формою і кольором. У початкових класах ці форми малюють найчастіше ...
... багато в чому залежить від висоти і конструкції стільця, нахилу робочого стола, розміщення інструментів на столі, рівня освітленості тощо. Звичайно, ці фактори в школі регулювати важко, особливо тоді, коли заняття з петриківського розпису проводяться у звичайних класах. Учитель повинен знати основні вимоги, які мають бути створені для нормального виконання графічних робіт. Так, висоту парти і сті ...
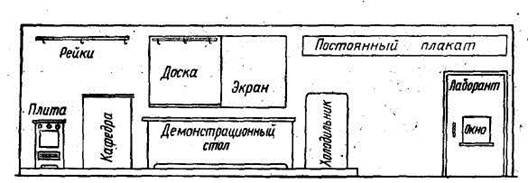
... дзеркала над демонстраційною плитою протягом багатьох років з успіхом використовуються в кулінарних училищах. 2.2 Експериментальна перевірка ефективності застосування технічних засобів навчання у навчально-виховному процесі при вивченні дисципліни «Кулінарія» Для перевірки результативності засвоєння знань студентами Чернігівського комерційного технікуму з використанням на заняттях технічних ...

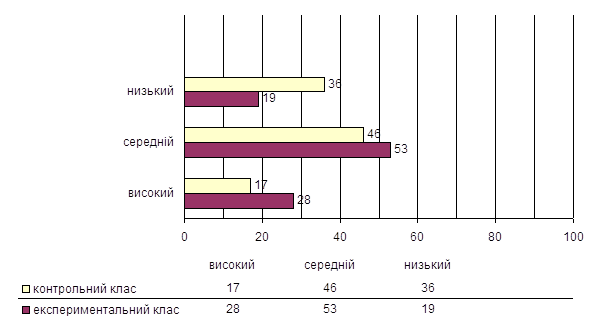


0 комментариев