Использование векторных и матричных операторов и функций

2.3 Использование векторных и матричных операторов и функций

2.3.1 Операции умножения и деления

а) умножение матрицы на скалярное число

Произведение матрицы А на число  (или числа  на матрицу А) называется матрица С того же размера, что и А, элементы которой равны произведению соответствующих элементов матрицы А на число .

С = А= А =

б) умножение вектора на скалярное число

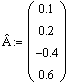
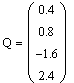
в) скалярное произведение двух векторов.

Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними.

г) умножение матрицы на вектор и матрицу.

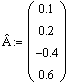
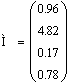
4 столбца

произведение определено в случае , т.е. когда число столбцов множимого равно числу строк множителя.

4 строки

При умножении единичной матрицы на матрицу А слева или справа получится матрица А:

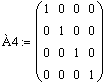
д) деление матрицы на скалярное число

2.3.2 Операции сложения.

а) в символьном виде

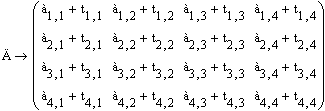
б) в числовом виде.

2.3.3 Транспонирование матриц и векторов

Пользуемся панелью векторов и матриц. Значок М или <Ctrl>+<1>.

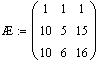
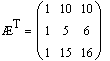
Вектор-столбец транспонирован в строку

Строки матриц транспонированы в столбцы.