Навигация
Разложение матрицы на треугольную, ортогональную
2.3.15 Разложение матрицы на треугольную, ортогональную
L U-разложением матрицы А, или треугольным разложением, называется матричное разложение вида P A=L U и, где L и U — нижняя и верхняя треугольные матрицы (нули выше диагонали и ниже), соответственно. P,A,L,U — квадратные матрицы одного порядка.
· lu(A) — LU-разложение матрицы;
o А — квадратная матрица.
Фактически, треугольное разложение матрицы системы линейных уравнений производится при ее решении численным методом Гаусса.
Функция LU-разложения выдает составную матрицу. Выделить матрицы P,L,U несложно при помощи встроенной функции submatrix.
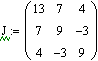
![]()

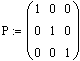

![]()
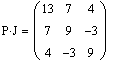
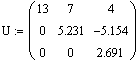
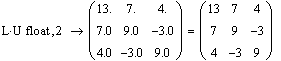
QR-разложением матрицы А называется разложение вида A=Q R, где Q — ортогональная матрица, а R — верхняя треугольная матрица.
· qr(A) —QR-разложение;
o А — вектор или матрица любого размера.
Результатом действия функции qr(A) является матрица L, составленная из матриц Q и R, соответственно. Чтобы выделить сами матрицы QR-разложения, необходимо применить функцию выделения подматрицы submatrix.
![]()


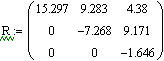

2.4 Использование матричных функций
2.4.1 Собственные значения и векторы собственных значений матрицы
а) Определение собственных значений с помощью характеристического уравнения
Пусть X и Y – векторы. А- квадратная матрица, оператор преобразования Х в Y. Часто бывают случаи, когда необходимо найти вектор ҳ и значение скаляра λ такие , что А· ҳ = λ·ҳ. Такое уравнение имеет решения в виде собственных значений λ1, λ2,... и соответствующих им собственных векторов x1, х2,...Значение скаляра λ носит название собственных значений квадратной матрицы А. Его можно получить из характеристического уравнения матрицы А.
Характеристическое уравнение матрицы имеет вид:
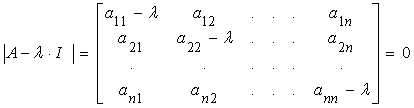
Его корни: ![]() называются собственными числами матрицы А.
называются собственными числами матрицы А.
Их сумма равна сумме диагональных элементов матрицы А (или следу матрицы А)
![]()
Исходная  матрица:
матрица:
Функция identity (4) создаёт единичную матрицу размером 4*4
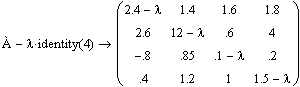

Находим корни характеристического уравнения:
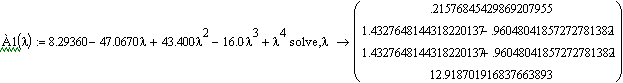
![]()
![]()
![]()
![]()

след сумма собственных чисел и матрицы
б) Определение вектора, элементами которого являются собственные значения матрицы с помощью функций Mathcad.
Для решения задач на собственные векторы и собственные значения в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы:
eigenvals(A) — вычисляет вектор, элементами которого являются собственные значения матрицы А; По умолчанию Mathcad отобразит три знака после запятой. Если необходимо увеличить точность собственных чисел матрицы, то необходимо воспользоваться командами: Format-Number главного меню и указать в окошечке Displayed Precision (3) желаемое число знаков после запятой (от 0 до 15).

![]()
![]()
![]()

![]()
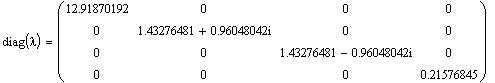
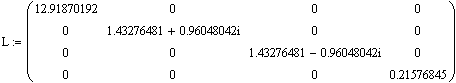
![]()
0 комментариев