Навигация
2.2 Практическая часть
Ручной счёт
Данные для расчета:
С≤16 Таблица 4| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Qi | 0.17 | 0.03 | 0.15 | 0.09 | 0.13 | 0.08 | 0.07 | 0.02 | 0.06 | 0.04 |
| с(xi) | 5 | 1 | 4 | 2 | 6 | 3 | 2 | 3 | 1 | 1 |
| hj | 0.034 | 0.03 | 0.0375 | 0.045 | 0.0217 | 0.0267 | 0.035 | 0.0067 | 0.06 | 0.04 |
Для удобства расчетов проранжируем таблицу 4 в порядке убывания hj и присвоим новые номера элементам, следующим образом:
Таблица 5
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| n | 9 | 4 | 10 | 3 | 7 | 1 | 2 | 6 | 5 | 8 |
| Qi | 0.06 | 0.09 | 0.04 | 0.15 | 0.07 | 0.17 | 0.03 | 0.08 | 0.13 | 0.02 |
| с(xi) | 1 | 2 | 1 | 4 | 2 | 5 | 1 | 3 | 6 | 3 |
| hj | 0.06 | 0.045 | 0.04 | 0.0375 | 0.035 | 0.034 | 0.03 | 0.0267 | 0.02167 | 0.0067 |
Для формирования таблицы 6 произведем расчеты:
1)
8
∑сj=19>b1 - ∑ cj∙xj=16-0=16;
j=1 xjЄS
7
∑сj=16£16;
j=1
7
∆с = с - ∑ сj∙xj- ∑сj=16-0-16=0
xjЄS j=1
Hs(x1) = q1+q2+q3+q4+q5+q6+q7+h8∆с = 0.61
8
∑сj=18>b1 - ∑ cj∙xj=16-0=16;
j=2 xjЄS
7
∑сj=15£16;
j=2
7
∆с = с - ∑ сj∙xj- ∑сj=16-0-15=1
xjЄSj=2
Hs(x1) = q2+q3+q4+q5+q6+q7+h8∆с = 0.5767
2)
8
∑сj=18>b1 - ∑ cj∙xj=16-1=15;
j=2 xjЄS
7
∑сj=15£15;
j=2
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-15=0
xjЄS j=2
Hs(x2) = q1+q2+q3+q4+q5+q6+q7+h8∆с = 0.61
8
∑сj=16>b1 - ∑ cj∙xj=16-1=15;
j=3 xjЄS
7
∑сj=13£15;
j=3
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-13=2
xjЄS j=3
Hs(x2) = q1+q3+q4+q5+q6+q7+h8∆с = 0.5734
3)
8
∑сj=16>b1 - ∑ cj∙xj=16-1-2=13;
j=3 xjЄS
7
∑сj=13£13;
j=3
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-13=0
xjЄS j=3
Hs(x3) = q1+q2+q3+q4+q5+q6+q7+h8∆с = 0.61
8
∑сj=15>b1 - ∑ cj∙xj=16-1-2=13;
j=4 xjЄS
7
∑сj=12£13;
j=4
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-12=1
xjЄS j=4
Hs(x3) = q1+q2+q4+q5+q6+q7+h8∆с = 0.5967
4)
8
∑сj=15>b1 - ∑ cj∙xj=16-1-2-1=12;
j=4 xjЄS
7
∑сj=12£12;
j=4
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-1-12=0
xjЄS j=4
Hs(x4) = q1+q2+q3+q4+q5+q6+q7+h8∆с = 0.61
9
∑сj=17>b1 - ∑ cj∙xj=16-1-2-1=12;
j=5 xjЄS
8
∑сj=11£12;
j=5
8
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-1-11=1
xjЄS j=5
Hs(x4) = q1+q2+q3+q5+q6+q7+q8+h9∆с = 0.56167
5)
8
∑сj=11>b1 - ∑ cj∙xj=16-1-2-1-4=8;
j=5 xjЄS
7
∑сj=8£8;
j=5
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-1-4-8=0
xjЄS j=5
Hs(x5) = q1+q2+q3+q4+q5+q6+q7+h8∆с = 0.61
8
∑сj=9>b1 - ∑ cj∙xj=16-1-2-1-4=8;
j=6 xjЄS
7
∑сj=6£8;
j=6
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-1-4-6=2
xjЄS j=6
Hs(x5) = q1+q2+q3+q4+q6+q7+h8∆с = 0.5934
6)
8
∑сj=9>b1 - ∑ cj∙xj=16-1-2-1-4-2=6;
j=6 xjЄS
7
∑сj=6£6;
j=6
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-1-4-2-6=0
xjЄS j=6
Hs(x6) = q1+q2+q3+q4+q5+q6+q7+h8∆с = 0.61
9
∑сj=10>b1 - ∑ cj∙xj=16-1-2-1-4-2=6;
j=7 xjЄS
8
∑сj=4£6;
j=7
7
∆с = с - ∑ сj∙xj- ∑сj=16-1-2-1-4-2-4=2
xjЄS j=6
Hs(x6) = q1+q2+q3+q4+q5+q7+q8+h9∆с = 0.56334
7) Cs = ∑ cj∙xj, проверяем условие С-Сs. Если с (xj)> С-Сs, то эти
xjЄS
элементы вводятся в множество Es.
Es = {x8,x9,x10}
с7=1>b1 - ∑ cj∙xj=16-1-2-1-4-2-5=1;
xjЄS
с7=1£1;
Условие не выполняется.
8) Ls = q1+q2+q3+q4+q5+q6+q7 = 0.61
Ls принимается в качестве приближенного решения L0. Так как все вершины дерева, для которых выполняется условие Hs£ L0, из дальнейшего рассмотрения исключаются, то процесс расчета прекращается.
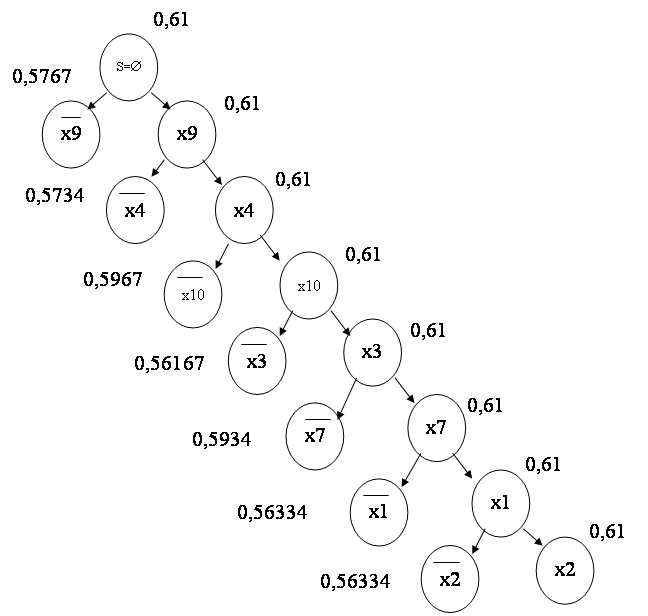
Таблица 6
|
| S | Es | Gs | Hs | xr | Hs(xr) | Hs(xr) | L0 |
| 1 | Æ | Æ | 1…10 | 0.61 | x1 | 0.61 | 0.5767 | |
| 2 | x1 | Æ | 2…10 | 0.61 | x2 | 0.61 | 0.5734 | |
| 3 | x1,x2 | Æ | 3…10 | 0.61 | x3 | 0.61 | 0.5967 | |
| 4 | x1,x2,x3 | Æ | 4…10 | 0.61 | x4 | 0.61 | 0.56167 | |
| 5 | x1,x2,x3,x4 | Æ | 5…10 | 0.61 | x5 | 0.61 | 0.5934 | |
| 6 | x1,x2,x3,x4,x5 | Æ | 6…10 | 0.61 | x6 | 0.61 | 0.56334 | |
| 7 | x1,x2,x3,x4,x5,x6 | 8,9,10 | 7 | 0.61 | x7 | 0.61 | 0.56334 | |
| 8 | x1,x2,x3,x4,x5,x6,x7 | 8,9,10 | Æ | - | - | - | - | 0.61 |
Для контроля системы необходимо использовать следующие параметры контроля: x1,x2,x3,x4,x5,x6,x7.
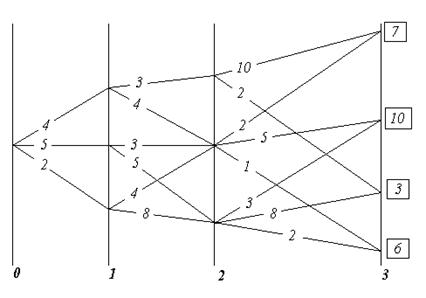
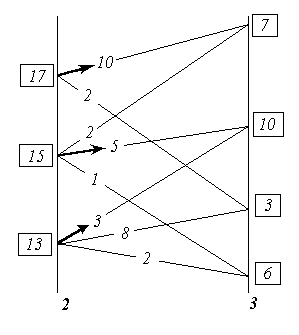
Перейдем на старую нумерацию элементов и построим дерево возможных вариантов решения. Оно представлено на рис.1. Около каждой вершины указана верхняя граница решения. Так как все эти оценки не превышают величины 0,61, то, следовательно, полученное решение L0 = 0,61 является оптимальным. Таким образом необходимо использовать следующие параметры контроля: x9,x4,x10,x3,x7,x1,x2.
 | |||
| |||
Листинг программы
program vetvi;
const
maxmatrix=1000;
maxsize=200;
type linear=array[1..10000] of integer;
label skip;
var matrix:array[1..1000] of pointer;
n:integer;
sizeofm:word;
q,w,e,r:integer;
start_m:integer;
sm:^linear;
bestx,besty:integer;
bz:integer;
ochered:array[1..1000] of
record
id:integer;
ocenka:integer;
end;
nochered:integer;
workm,workc:integer;
leftm,rightm:integer;
first,last:integer;
best:integer;
bestmatr:array[1..maxsize] of integer;
bestmatr1:array[1..maxsize] of integer;
curr:integer;
procedure swapo(a,b:integer);
begin
ochered[1000]:=ochered[a];
ochered[a]:=ochered[b];
ochered[b]:=ochered[1000];
end;
procedure addochered(id,ocenka:integer);
var
curr:integer;
begin
inc(nochered);
ochered[nochered].id:=id;
ochered[nochered].ocenka:=ocenka;
{Uravnoveshivanie ocheredi}
curr:=nochered;
while true do
begin
if curr=1 then break;
if ochered[curr].ocenka< ochered[curr div 2].ocenka
then
begin
swapo(curr,curr div 2);
curr:=curr div 2;
end
else break;
end;
end;
procedure getochered(var id,ocenka:integer);
var
curr:integer;
begin
id:=ochered[1].id;
ocenka:=ochered[1].ocenka;
ochered[1]:=ochered[nochered];
dec(nochered);
curr:=1;
while true do
begin
if (curr*2+1> nochered) then break;
if (ochered[curr*2].ocenka< ochered[curr].ocenka) or
(ochered[curr*2+1].ocenka<ochered[curr].ocenka) then
begin
if ochered[curr*2].ocenka> ochered[curr*2+1].ocenka
then
begin
swapo(curr*2+1,curr);
curr:=curr*2+1;
end
else
begin
swapo(curr*2,curr);
curr:=curr*2;
end;
end else break;
end;
end;
function getid:integer;
var q:integer;
qw:^linear;
begin
if memavail<10000 then
begin
q:=ochered[nochered].id;
{ exit;}
end else
begin
for q:=1 to maxmatrix do
if matrix[q]=nil then break;
getmem(matrix[q],sizeofm);
end;
qw:=matrix[q];
fillchar(qw^,sizeofm,0);
getid:=q;
end;
procedure freeid(id:integer);
begin
freemem(matrix[id],sizeofm);
matrix[id]:=nil;
end;
function i(x,y:integer):integer;
begin
i:=(y-1)*n+x+1;
end;
function simplize(id:integer):integer;
var
q,w:integer;
t:^linear;
add:integer;
min:integer;
begin
t:=matrix[id];
add:=0;
for q:=1 to n do
begin
min:=maxint;
for w:=1 to n do
if t^[i(w,q)]< >-1 then
if min> t^[i(w,q)] then min:=t^[i(w,q)];
if min<>0 then
for w:=1 to n do
if t^[i(w,q)]< >-1 then
dec(t^[i(w,q)],min);
if min>32000 then min:=0;
inc(add,min);
end;
for q:=1 to n do
begin
min:=maxint;
for w:=1 to n do
if t^[i(q,w)]< >-1 then
if min> t^[i(q,w)] then min:=t^[i(q,w)];
if min<>0 then
for w:=1 to n do
if t^[i(q,w)]< >-1 then
dec(t^[i(q,w)],min);
if min>32000 then min:=0;
inc(add,min);
end;
simplize:=add;
end;
function bestziro(id:integer):integer;
var
t:^linear;
q,w,e,x,y:integer;
min1,min2:integer;
l1,l2:array[1..maxsize] of integer;
begin
t:=matrix[id];
fillchar(l1,sizeof(l1),0);
fillchar(l2,sizeof(l2),0);
for q:=1 to n do
begin
min1:=maxint;min2:=maxint;
for w:=1 to n do
if t^[i(w,q)]< >-1 then
begin
if min2> t^[i(w,q)] then min2:=t^[i(w,q)];
if min1> min2 then
begin
e:=min1;
min1:=min2;
min2:=e;
end;
end;
if min1<>0 then min2:=0;
if min2>32000 then min2:=0;
l2[q]:=min2;
end;
for q:=1 to n do
begin
min1:=maxint;min2:=maxint;
for w:=1 to n do
if t^[i(q,w)]< >-1 then
begin
if min2> t^[i(q,w)] then min2:=t^[i(q,w)];
if min1> min2 then
begin
e:=min1;
min1:=min2;
min2:=e;
end;
end;
if min1<>0 then min2:=0;
if min2>32000 then min2:=0;
l1[q]:=min2;
end;
bz:=-32000;
bestx:=0;besty:=0;
for y:=n downto 1 do
for x:=1 to n do
if (t^[i(x,y)]=0) then
if l1[x]+l2[y]> bz then
begin
bestx:=x;
besty:=y;
bz:=l1[x]+l2[y];
end;
bestziro:=bz;
end;
begin
assign(input,'input.txt');
assign(output,'vetvi.out');
reset(input);
rewrite(output);
nochered:=0;
read(n);
sizeofm:=n*(n+2)*2+2;
start_m:=getid;
sm:=matrix[start_m];
for q:=1 to n do
for w:=1 to n do
read(sm^[i(w,q)]);
addochered(start_m,0);
{ ;
bestziro(start_m);}
{Sobstvenno reshenie}
best:=maxint;
while true do
begin
if nochered=0 then break;
getochered(workm,workc);
{process MATRIX}
inc(workc,simplize(workm));
if workc> best then goto skip;
sm:=matrix[workm];
if sm^[1]=n-1 then
begin
best:=workc;
for q:=1 to n do
begin
bestmatr [q]:=sm^[i(q,n+2)];
bestmatr1[q]:=sm^[i(q,n+1)];
end;
goto skip;
end;
q:=bestziro(workm);
if q=-32000 then goto skip;
{Pravaia vetka}
if(bestx=0) or (besty=0) then goto skip;
rightm:=getid;
move(matrix[workm]^,matrix[rightm]^,sizeofm);
sm:=matrix[rightm];
sm^[i(bestx,besty)]:=-1;
addochered(rightm,workc+q);
{Levaia vetka}
leftm:=getid;
move(matrix[workm]^,matrix[leftm]^,sizeofm);
sm:=matrix[leftm];
{Dobavliaetsia rebro iz bestx v besty}
inc(sm^[1]);
sm^[i(bestx,n+2)]:=besty;
sm^[i(besty,n+1)]:=bestx;
first:=bestx;last:=besty;
if sm^[1]< >n-1 then
begin
while true do
begin
if sm^[i(last,n+2)]=0 then break;
last:=sm^[i(last,n+2)];
end;
while true do
begin
if sm^[i(first,n+1)]=0 then break;
first:=sm^[i(first,n+1)];
end;
sm^[i(last,first)]:=-1;
sm^[i(first,last)]:=-1;
sm^[i(besty,bestx)]:=-1;
end;
for w:=1 to n do
begin
sm^[i(w,besty)]:=-1;
sm^[i(bestx,w)]:=-1;
end;
addochered(leftm,workc);
skip:
{Free Matrix}
freeid(workm);
end;
{ freeid(start_m);}
if best=maxint then
begin
writeln('Путь не существует');
end else
begin
writeln('Длина пути:',best);
for q:=1 to n do
if bestmatr[q]=0 then break;
e:=q;
for curr:=1 to n do
if bestmatr[curr]=q then break;
while true do
begin
write(curr,' ');
curr:=bestmatr1[curr];
if curr=0 then
begin
writeln(e);
break;
end;
end;
end;
close(input);
close(output);
end.
Вывод
При решении поставленной задачи оба метода дали одинаковый результат, что показывает правильность понимания и выполнения курсовой работы. Таким образом, необходимо использовать следующие параметры контроля: x9,x4,x10,x3,x7,x1,x2.
Метод динамического программирования достаточно прост для выполнения, но имеет существенный недостаток: при его использовании для счёта вручную возникают вычислительные трудности даже для простых систем.
Метод ветвей и границ является более сложным для понимания, но он оказался проще при ручном счёте. Недостатком является большая сложность программирования метода.
Литература
1. Селезнев А.В., Добрица Б.Т., Убар Р.Р. «Проектирование автоматизированных систем контроля бортового оборудования летательных аппаратов» стр. 90-95
2. Алексеев О.Г. «Комплексное применение методов дискретной оптимизации» стр. 18-25
Похожие работы
... По теореме 9.3 в силу результатов шагов 3 и 8. (Шаг 10). Имеет место свойство (9.4) по теореме 9.5 в силу результатов шагов 1 и 9. Литература к лекции 9. 9.1. С.А. Абрамов. Элементы программирования. - М.: Наука, 1982. С. 85-94. 9.2. М. Зелковец, А. Шоу, Дж. Гэннон. Принципы разработки программного обеспечения. - М.: Мир, 1982. С. 98-105. Лекция 10. ТЕСТИРОВАНИЕ И ОТЛАДКА ПРОГРАММНОГО ...
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
... проектирования. Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС. Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью ...

0 комментариев