Представлення даних в ЕОМ

1.2 Представлення даних в ЕОМ

Подання (кодування) даних.

Щоб працювати з даними різних видів, необхідно уніфікувати форму їхнього подання, а це можна зробити за допомогою кодування. Кодуванням ми займаємося досить часто, наприклад, людина мислить досить розпливчастими поняттями, і, щоб донести думка від однієї людини до іншої, застосовується мова. Мова - це система кодування понять. Щоб записати слова мови, застосовується знову ж кодування - абетка. Проблемами універсального кодування займаються різні галузі науки, техніки, культури. Згадаємо, що креслення, ноти, математичні викладення є теж деяким кодуванням різних інформаційних об'єктів. Аналогічно, універсальна система кодування потрібно для того, щоб велика кількість різних видів інформації можна було б обробити на комп'ютері.

Підготовка даних для обробки на комп'ютері (подання даних) в інформатиці має свою специфіку, пов'язану з електронікою. Наприклад, ми хочемо проводити розрахунки на комп'ютері. При цьому нам доведеться закодувати цифри, якими записані числа. На перший погляд, представляється цілком природним кодувати цифру нуль станом електронної схеми, де напруга на деякому елементі буде дорівнює 0 вольтів, цифру одиниця - 1 вольтів, двійку - 2 вольтів і т.д., дев'ятку - 9 вольтів. Для запису кожного розряду числа в цьому випадку буде потрібно елемент електронної схеми, що має десять станів. Однак елементна база електронних схем має розкид параметрів, що може привести до появи напруги, скажемо 3,5 вольт, а воно може бути витлумачені і як трійка і як четвірка, тобто буде потрібно на рівні електронних схем "пояснити" комп'ютеру, де закінчується трійка, а де починається четвірка. Крім того, прийде створювати досить непрості електронні елементи для виробництва арифметичних операцій із числами, тобто на схемному рівні повинні бути створені та б- . особи множення - 10 х 10 = 100 схем і таблиця додавання - теж 100 схем. Для електроніки 40-х рр. (час, коли з'явилися перші обчислювальні машини) це було непосильне завдання. Ще складніше виглядало б завдання обробки текстів, адже російський алфавіт має 33 букви. Очевидно, такий шлях побудови обчислювальних систем не заможний.

У той же час досить просто реалізувалися електронні схеми із двома стійкими станами: є струм - 1, немає струму - 0; є електричне (магнітне) поле 1, немає - 0. Погляди створювачів обчислювальної техніки були звернені на двійкове кодування як універсальну форму подання даних для подальшої г обробки їхніми засобами обчислювальної техніки. Передбачається, що дані розташовуються в деяких осередках, що представляють упорядковану сукупність із двійкових розрядів, а розряд може тимчасово містити один зі станів - 0 або 1. Тоді . групою із двох двійкових розрядів (двох біт) можна закодувати 2² = 4 різні комбінації кодів (00, 01, 10, 11); аналогічно, три ц біти дадуть 2³ = 8 комбінацій, вісім біт або 1 байт - 2⁸ = 256 і т.д. .

Отже, внутрішня абетка комп'ютера дуже бідна, містить усього два символи: 0, 1, тому й виникає проблема подання . усього різноманіття типів даних - чисел, текстів, звуків, графічних зображень, відео й ін. - тільки цими двома символами, з метою подальшої обробки засобами обчислювальної техніки. Питання подання деяких типів даних ми розглянемо у наступних параграфах.

Подання чисел в двійковому коді

Існують різні способи запису чисел, наприклад: можна записати число у вигляді тексту - сто двадцять три; римські системи числення - CXXІІІ; арабської – 123.

Системи числення.

Сукупність прийомів запису й найменування чисел називається системою числення.

Числа записуються за допомогою символів, і по кількості символів, використовуваних для запису числа, системи числення підрозділяються на позиційні й непозиційні. Якщо для запису числа використається нескінченна безліч символів, то система числення називається непозиційної. Прикладом непозиційної системи числення може служити римська. Наприклад, для запису числа один використається буква Й, два й три виглядають як сукупності символів ІІ, ІІІ, але для запису числа п'ять вибирається новий символ V, шість - VІ, десять - уводиться символ - X, сто - С, тисяча - М т.д. Нескінченний ряд чисел зажадає нескінченного числа символів для запису чисел. Крім того, такий спосіб запису чисел приводить до дуже складних правил арифметики.

Позиційні системи числення для запису чисел використають обмежений набір символів, називаних цифрами, і величина числа залежить не тільки від набору цифр, але й від того, у якій послідовності записані цифри, тобто від позиції, займаною цифрою, наприклад, 125 й 215. Кількість цифр, використовуваних для запису числа, називається підставою системи числення, надалі його позначимо q.

У повсякденному житті ми користуємося десятковою позиційною системою числення, q = 10, тобто використається 10 цифр: 0 12 3 4 5 6 7 8 9.

Розглянемо правила запису чисел у позиційній десятковій системі числення. Числа від 0 до 9 записуються цифрами, для запису наступного числа цифри не існує, тому замість 9 пишуть 0, але левее нуля утвориться ще один розряд, називаний старшим, де записується (додається) 1, у результаті виходить 10. Потім підуть числа 11, 12, але на 19 знову молодший розряд заповниться й ми його знову замінимо на 0, а старший розряд збільшимо на 1, одержимо 20. Далі за аналогією 30, 40...90 , 91, 92 ... до 99. Тут заповненими виявляються два розряди відразу; щоб одержати наступне число, ми заміняємо обоє на 0, а в старшому розряді, тепер уже третьому, поставимо 1 (тобто одержимо число 100) і т.д. Очевидно, що, використовуючи кінцеве число цифр, можна записати кожне як завгодно велике число. Помітимо також, що виробництво арифметичних дій у десятковій системі числення досить просто.

Число в позиційній системі числення з підставою q може бути представлене у вигляді полінома по ступенях q. Наприклад, у десятковій системі ми маємо число:

123,45 = 1*102+ 2*101+ 3*100+ 4*10-1 + 5*10-2,

а в загальному виді це правило запишеться так (формула 1.):

X(q)= xn-1*qn-1+xn-2*qn-2 +..+ x1*q1+ x0*q0+ x-1*q-1+..+ x-m*q-m

тут X(q) - запис числа в системі числення з підставою q;

xi - натуральні числа менше q, тобто цифри;

n - число розрядів цілої частини;

m - число розрядів дробової частини.

Записуючи ліворуч праворуч цифри числа, ми одержимо закодованій запис числа в q-ичній системі числення (формула 2.):

X(q)= xn-1*xn-2*x1*x0* x-1* x-2* x-m

В інформатиці, внаслідок застосування електронних засобів обчислюваль-ної техніки, велике значення має двійкова система числення, q = 2. На ранніх етапах розвитку обчислювальної техніки арифметичні операції з дійсними числами проводилися у двійковій системі через простоту їхньої реалізації в електронних схемах обчислювальних машин. Наприклад, таблиця додавання й таблиця множення будуть мати по чотирьох правила (табл. 1).

Таблиця 1. Правила таблиці додавання та таблиці множення

0 + 0 = 0	0 x 0 = 0
0 + 1 = 1	0 x 1= 0
1 + 0 =1	1 x 0 = 0
1 + 1 = 1	1 x 1 = 1

А виходить, для реалізації порозрядної арифметики в комп'ютері будуть потрібні замість двох таблиць по сто правил у десятковій системі числення дві таблиці по чотирьох правила у двійковій. Відповідно на апаратному рівні замість двохсот електронних схем - вісім.

Але запис числа у двійковій системі числення довший запису того ж числа в десятковій системі числення в log₂10 разів (приблизно в 3,3 рази). Це громіздко й не зручно для використання, тому що звичайно людина може одночасно сприйняти не більше п'яти-семи одиниць інформації, тобто зручно буде користуватися такими системами числення, у яких найбільше часто використовувані числа (від одиниць до тисяч) записувалися б одними-чотирма цифрами. Як це буде показано далі, переклад числа, записаного у двійковій системі числення, у восьмеричну й шістнадцятеричну дуже сильно спрощується в порівнянні з перекладом з десяткової у двійкову. Запис же чисел у них у три рази коротше для восьмеричної й у чотири для шістнадцятеричної системи, чим у двійкової, але довжини чисел у десяткової, восьмеричної й шістнадцятеричної системах числення будуть розрізнятися ненабагато. Тому, поряд із двійковою системою числення, в інформатиці мають ходіння восьмерична й шістнадцятерична системи числення.

Восьмерична система числення має вісім цифр: 0 1 2 3 4 5 6 7. Шістнадцятерична - шістнадцять, причому перші 10 цифр збігаються за написанням із цифрами десяткової системи числення, а для позначення шести цифр, що залишилися, застосовуються більші латинські букви, тобто для шістнадцятеричної системи числення одержимо набір цифр: 0123456789ABCDEF.

Якщо з контексту не ясно, до якої системи числення ставиться запис, то підстава системи записується після числа у вигляді нижнього індексу. Наприклад, те саме число 231, записане в десятковій системі, запишеться у двійкової, восьмеричної й шістнадцятеричної системах числення в такий спосіб:

231(10) = 11100111(2) = 347(8) = Е7

Запишемо початок натурального ряду в десятковій, двійковій, восьмеричній, шістнадцятеричній системах числення (табл. 2).

Таблиця 2. Натуральний ряд чисел у різних системах числення.

Десяткова	Двійкова	Восьмерична	Шістнадцятерична
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
Десяткова	Двійкова	Восьмерична	Шістнадцятерична
10	1010	12	А
11	1011	13	В
12	1100	14	С
13	1101	15	D
14	1110	16	Е
15	1111	17	F

Подання чисел у двійковому коді.

Подання чисел у пам'яті комп'ютера має специфічну особливість, пов'язану з тим, що в пам'яті комп'ютера вони повинні розташовуватися в байтах - мінімальних по розмірі адресуємих (тобто до них можливе обіг) комірках пам'яті. Очевидно, адресою числа варто вважати адреса першого байта. У байті може втримуватися довільний код з восьми двійкових розрядів, і завдання подання полягає в тім, щоб указати правила, як в одному або декількох байтах записати число.

Дійсне число багатообразне у своїх "споживчих властивостях". Числа можуть бути цілі точні, дробові точні, раціональні, ірраціональні, дробові наближені, числа можуть бути позитивними й негативними. Числа можуть бути "карликами", наприклад, маса атома, "гігантами", наприклад, маса Землі, реальними, наприклад, кількість студентів у групі, вік, ріст. І кожне з перерахованих чисел зажадає для оптимального подання в пам'яті своя кількість байтів.

Очевидно, єдиного оптимального подання для всіх дійсних чисел створити неможливо, тому творці обчислювальних систем пішли по шляху поділу єдиного по суті безлічі чисел на типи (наприклад, цілі в діапазоні від ... до ..., наближені із плаваючою крапкою з кількістю значущих цифр ... і т.д.). Для кожного окремо типу створюється власний спосіб подання.

Цілі числа. Цілі позитивні числа від 0 до 255 можна представити безпосередньо у двійковій системі числення (двійковому коді). Такі числа будуть займати один байт у пам'яті комп'ютера (табл. 3).

Таблиця 3. Двійковій код цілих чисел.

Число	Двійковий код числа
0	0000 0000
1	0000 0001
2	0000 0010
3	0000 0011
…	…
255	1111 1111

У такій формі подання легко реалізується на комп'ютерах двійкова арифметика.

Якщо потрібні й негативні числа, то знак числа може бути закодований окремим битому, звичайно це старший біт; нуль інтерпретується як плюс, одиниця як мінус. У такому випадку одним байтом може бути закодовані цілі числа в інтервалі від -127 до +127, причому двійкова арифметика буде трохи ускладнена, тому що в цьому випадку існують два коди, що зображують число нуль 0000 0000 й 1000 0000, і в комп'ютерах на апаратному рівні це буде потрібно передбачити. Розглянутий спосіб подання цілих чисел називається прямим кодом. Положення з негативними числами трохи спрощується, якщо використати, так званий, додатковий код. У додатковому коді позитивні числа збігаються з позитивними числами в прямому коді, негативні ж числа виходять у результаті вирахування з 1 0000 0000 відповідного позитивного числа. Наприклад, число -3 одержить код:

_ 1 0000 0000

0000 0011

1111 1101

У додатковому коді добре реалізується арифметика, тому що кожен наступний код виходить із попереднім додатком одиниці з точністю до біта в дев'ятому розряді. Наприклад

5-3 = 5 + (-3)

0000 0101

1111 1101

1 0000 0010, тобто, відкидаючи підкреслений старший розряд, одержимо 2.

Аналогічно цілі числа від 0 так 65536 і цілі числа від -32768 до 32767 у двійковій (шістнадцатеричної) системі числення представляються у двобайтових осередках. Існують подання цілих чисел й у чотирьобайтових осередках.

Дійсні числа. Дійсні числа в математику представляються кінцевими або нескінченними дробами, тобто точність подання чисел не обмежена. Однак у комп'ютерах числа зберігаються в регістрах і комірках пам'яті, які являють собою послідовність байтів з обмеженою кількістю розрядів. Отже, нескінченні або дуже довгі числа усікаються до деякої довжини й у комп'ютерному поданні виступають як наближені. У більшості систем програмування в написанні дійсних чисел ціла й дробова частини розділяються не комі, а крапкою.

Для подання дійсних чисел, як дуже маленьких, так і дуже більших, зручно використати форму запису чисел у вигляді добутку у формулі 3.

X = m * q^p

де m - мантиса числа;

q - підстава системи числення;

р - ціле число, називане порядком.

Такий спосіб запису чисел називається поданням числа із плаваючою крапкою.

Тобто число 4235,25 може бути записане в одному з видів:

4235,25 = 423,525 – 10¹ = 42,3525 – 10² = 4,23525 – 10³ = 0,423525 – 10⁴.

Очевидно, таке подання не однозначно. Якщо мантиса 1 / q < |m| < q (0,1 < |m| < 1 для десяткової системи числення), то подання числа стає однозначним, а така форма називається нормалізованої. Якщо "плаваюча" крапка розташована в мантисі перед першою значущою цифрою, то при фіксованій кількості розрядів, відведених під мантису, забезпечується запис максимальної кількості значущих цифр числа, тобто максимальна точність.

Дійсні числа в комп'ютерах різних типів записуються по-різному, проте існує кілька міжнародних стандартних форматів, що розрізняються по точності, але мають однакову структуру. Розглянемо на прикладі числа, що займає 4 байти (мал. 9).

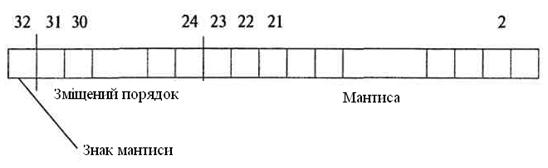
Малюнок 9. Формат числа, що займає 4 байти

Перший біт двійкового подання використається для кодування знака мантиси. Наступна група біт кодує порядок числа, а біти, що залишилися, кодують абсолютну величину мантиси. Довжини порядку й мантиси фіксуються.

Порядок числа може бути як позитивним, так і негативним. Щоб відбити це у двійковій формі, величина порядку представляється у вигляді суми щирого порядку й константи, рівній абсолютній величині максимального по модулі негативного порядку, називаної зсувом. Наприклад, якщо порядок може приймати значення від -128 до 127 (8 біт), тоді, вибравши як змішання 128, можна представити діапазон значень порядку від 0 (-128+128, порядок + зсув) до 255 (127+128),

Тому що мантиса нормалізованого числа завжди починається з нуля, деякі схеми подання його лише мають на увазі, використовуючи зайвий розряд для підвищення точності подання мантиси.

Використання зміщеної форми дозволяє робити операції над порядками як над беззнаковими числами, що спрощує операції порівняння, додавання й вирахування порядків, а також спрощує операцію порівняння самих нормалізованих чисел.

Чим більше розрядів приділяється під запис мантиси, тим вище точність подання числа. Чим більше розрядів займає порядок, тим ширше діапазон від найменшого відмінного від нуля числа до найбільшого числа, представимого в комп'ютері при заданому форматі.

Речовинні числа в пам'яті комп'ютера, залежно від необхідної точності (кількості розрядів мантиси) і діапазону значень (кількості розрядів порядку), займають від чотирьох до десяти байтів. Наприклад, чотирьобайтове речовинне число має 23 розряду мантиси (що відповідає точності числа 7-8 десяткових знаків) і 8 розрядів порядку (забезпечуючи діапазон значень 10±38). Якщо речовинне число займає десять байтів, то мантисі приділяється 65 розрядів, а порядку - 14 розрядів. Це забезпечує точність 19-20 десяткових знаків мантиси й діапазон значень 10±4931.

Поняття типу даних. Як уже говорилося, мінімально адресуемою одиницею пам'яті є байт, але подання числа вимагає більшого обсягу. Очевидно, такі числа займуть групу байт, а адресою числа буде адреса першого байта групи. Отже, довільно взятий з пам'яті байт нічого нам не скаже про те, частиною якого інформаційного об'єкта він є - цілого числа, числа із плаваючої коми або команди. Резюмуючи вищесказане, можна зробити висновок, що крім завдання подання даних у двійковому коді, паралельно вирішується зворотне завдання - завдання інтерпретації кодів, тобто як з кодів відновити первісні дані.