Навигация
Линейное однородное дифференциальное уравнение с постоянными коэффициентами
2.7.7. Линейное однородное дифференциальное уравнение с постоянными коэффициентами
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами имеет вид
![]() (5)
(5)
Его решение будем искать в виде y=ekx. Тогда y’=kekx, y’’=k2ekx, …, y(n)=knekx. Подставим это в исходное дифференциальное уравнение и получим так называемое характеристическое уравнение для дифференциального уравнения (5):
knekx+…+a2k2ekx+a1kekx+a0ekx=0
или, разделив это уравнение на ekx, так как он ни при каких x не равен нулю, получаем:
kn+…+a2k2+a1k+a0=0
Решив это уравнение относительно k, мы получим n корней, которые могут быть как действительными, так и мнимыми. В зависимости от вида корней характеристического уравнения мы будем иметь различные виды решения дифференциального уравнения:
1. Некоторые ki, …, kj из всего множества корней характеристического уравнения – действительные и различные числа. Тогда каждому km из этого множества будет соответствовать решение в виде: ym=cmekmx.
2. Некоторые ki,…, k2j – комплексные и различные. Тогда каждой паре km;m+1=am±bmi будет соответствовать решение ym=cmeamxcos(bmx); ym+1=eamxsin(bmx).
3. Среди решений характеристического уравнения есть корень ki кратности m. Ему будут соответствовать решения: yi=ciekix, yi+1=xci+1ekix, …, yi+m=xm-1ci+mekix.
4. Среди решений характеристического уравнения есть 2 комплексных корня ki;i+1=ai±bii кратности m. Им будут соответствовать решения yi=cieaixcos(bix); yi+1=ci+1eaixsin(bix); yi+2=xci+2eaixcos(bix) ; yi+3=xci+3eaixsin(bix) ; … ; yi+m=x2m-1cieaixcos(bix); yi+m=x2m-1 ´
´ci+1eaixsin(bix).
Однако, как было сказано выше, совокупность всех решений {y(x)} образует линейное пространство размерности n, так как решения этой системы являются линейно-независимыми и образуют базис. Это значит, что линейная комбинация решений линейного дифференциального уравнения также будет являться решением. Следовательно, общее решение данного линейного однородного дифференциального уравнения n-го порядка (5) с постоянными коэффициентами можно представить как линейную комбинацию решений, соответствующих каждому корню (или паре корней) характеристического уравнения.
2.7.8. Линейное неоднородное дифференциальное уравнение
Линейное неоднородное дифференциальное уравнение имеет вид
y(n)+Pn-1(x)y(n-1)+…+P2y’+P1y+P0=f(x), (6)
где P0(x), P1(x),…, Pn-1(x), f(x) – некоторые непрерывные функции, непрерывные по x и удовлетворяющие условию Липшица по x. Соответствующее ему однородное дифференциальное уравнение имеет вид
y(n)+Pn-1(x)y(n-1)+…+P2y’+P1y+P0=0, (7).
Если дифференциальное уравнение (6) имеет частное решение yв(x) и общее решение yс=c1y1+c2y2+…+cnyn, то общее решение дифференциального уравнения (6) равно сумме частного решения yв и общего решения линейного однородного дифференциального уравнения (7) yc: y=yc+yв.
Методика нахождения общего решения линейного однородного уравнения была изложена выше. Здесь мы рассмотрим нахождение частного решения линейного неоднородного уравнения.
Частное решение будет зависеть от вида правой части f(x). В общем случае трудно найти частное решение для любой функции f(x). Однако на практике применяются следующие виды функции f(x):
1. f(x)=P(x)eax, где P(x) – некоторый многочлен. Тогда частное решение ищется в виде:
1) yч=xmQ(x)eax, если a – m-кратный корень характеристического уравнения;
2) yч=Q(x)eax, если a – не корень характеристического уравнения,
где Q(x) – многочлен той же степени, что и P(x), но с неопределенными коэффициентами.
2. f(x)=(Pn(x)cos(bx)+Lm(x)sin(bx))eax, где Pn(x) и Lm(x) – некоторые многочлены. Тогда частное решение ищется в виде:
1) yч=(Mn(x)cos(bx)+Nn(x)sin(bx))eax, если (a±bi) – не корень характеристического уравнения;
2) yч=xm(Mn(x)cos(bx)+Nn(x)sin(bx))eax, если (a±bi) – m-кратный корень характеристического уравнения,
где Mn(x) и Nn(x) – многочлены, степень которых равна наивысшей степени многочленов Pn(x) и Lm(x).
После выбора вида частного решения подставляем его в исходное дифференциальное уравнение. При этом неизвестные коэффициенты полиномов находим по методу неопределенных коэффициентов, который заключается в том, что неизвестные коэффициенты ищутся из условия равенства коэффициентов при одинаковых слагаемых, например, при x, при x2, при x3cos(bx) и т. д.
3. Дифференциальные уравнения при описании непрерывных систем
3.1. Составление и линеаризация дифференциальных уравнений элементов системы
В установившемся состоянии зависимость выходной величины элемента системы от входной задается статической характеристикой элемента. Как правило, статические характеристики элементов нелинейны. Статические характеристики могут быть получены из дифференциальных уравнений элементов системы.
Пусть дифференциальное уравнение, описывающее поведение элемента, имеет вид
![]() (1)
(1)
Тогда статическая характеристика этого элемента задается уравнением в неявной форме
![]() (2)
(2)
то есть для ее получения в уравнении (1) следует положить x=const и g=const.
Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным, если дифференциальное уравнение нелинейно, то элемент называется нелинейным. Из-за нелинейности статических характеристик уравнения элементов системы в большинстве случаев являются нелинейными.
Для упрощения анализа, когда это возможно, приближенно заменяют нелинейные дифференциальные уравнения такими линейными уравнениями, решения которых с достаточной степенью точности совпадают с решениями нелинейных уравнений. Этот процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией. Обычно линеаризация нелинейного уравнения производится относительно некоторого установившегося состояния элемента системы.
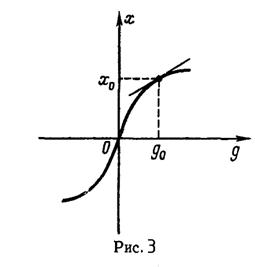
Если дифференциальное уравнение элемента нелинейно из-за нелинейности его статической характеристики, то линеаризация уравнения сводится к замене нелинейной характеристики элемента x=ф(g) некоторой линейной функцией x=ag+b. Аналитически эта замена производится с помощью разложения в ряд Тейлора функции x=y(g) в окрестности точки, соответствующей установившемуся состоянию и отбрасывания всех членов, содержащих отклонение Dg входной величины элемента в степени выше первой. Геометрически это означает замену кривой x=ф(g) касательной, проведенной к кривой в точке (х0, g0), соответствующей установившемуся состоянию работы элемента (рис. 3).
В других случаях линеаризация производится путем проведения секущей, мало отклоняющейся от функции x=ф(g) в требуемом диапазоне изменения входной величины элемента.
Назовем нелинейные статические характеристики, линеаризуемые в требуемом диапазоне изменения входной величины указанным выше способом, несущественно нелинейными характеристиками. Наряду с линеаризуемыми характеристиками имеются такие характеристики, которые не поддаются такой линеаризации. К ним относятся, например, характеристики, не разлагаемые в ряд Тейлора в окрестности точки установившегося состояния. Такие характеристики будем называть существенно нелинейными.
Рассмотрим подробнее процесс линеаризации нелинейного уравнения элемента с помощью ряда Тейлора. Пусть поведение элемента описывается нелинейным дифференциальным уравнением (1). Тогда установившееся состояние элемента характеризуется уравнением (2). Пусть g0 и х0 — значения установившегося состояния. Тогда координаты g и х можно записать в виде х=х0+Dx, g=g0+Dg, где Dg и Dx — отклонения координат g и x от установившегося состояния. Уравнение (1) в отклонениях имеет вид
![]()
Разложим левую часть этого уравнения в ряд Тейлора относительно точки (0, 0, х0, g0):
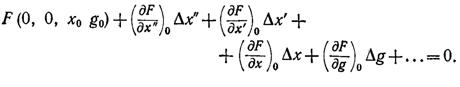
В левой части этого равенства не выписаны члены, содержащие отклонения Dg и Dx и их производные в степени выше первой. Частные производные в левой части этого уравнения представляют собой некоторые числа, величины которых зависят от вида функции F(x", x', x, g) и значений координат g0 и х0.
Считая отклонения Dg, Dх от установившегося состояния, а также их производные по времени малыми и полагая, что функция F(x", x', x, g) достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в этом уравнении все члены, которые содержат отклонения Dg и Dх, а также их производные в степени выше первой. Полученное уравнение
![]()
является линейным дифференциальным уравнением с постоянными коэффициентами
![]()
Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x", x', x, g) в окрестности точки, соответствующей установившемуся состоянию. Линеаризованное уравнение приближенно заменяет нелинейное уравнение (1) лишь в некоторой малой окрестности точки (0, 0, х0, g0). Величина этой окрестности зависит от гладкости функции F(x", x', x, g) в этой точке, т. е. от величин производных порядка выше первого этой функции в точке (0, 0, х0, g0). Как правило, с помощью линеаризованного уравнения можно исследовать поведение элемента системы лишь при малых отклонениях входной и выходной координаты от установившегося состояния. Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x", x', x, g) в окрестности точки, соответствующей установившемуся состоянию. Линеаризованное уравнение приближенно заменяет нелинейное уравнение (1) лишь в некоторой малой окрестности точки (0, 0, х0, g0). Величина этой окрестности зависит от гладкости функции F(x", x', x, g) в этой точке, т. е. от величин производных порядка выше первого этой функции в точке (0, 0, х0, g0). Как правило, с помощью линеаризованного уравнения можно исследовать поведение элемента системы лишь при малых отклонениях входной и выходной координаты от установившегося состояния.
Похожие работы
... . , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5]. Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... - α) / (2 + α)) yk - 1 + (α/ (2 + α)) (xk + xk - 1). (9) В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов. Моделирование линейных замкнутых систем Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со ...




0 комментариев