Н.В. Перцев, Омский государственный педагогический университет, кафедра математического анализа
1. ВведениеВ работе автора [1] предложена математическая модель, описывающая динамику численности некоторых популяций с ограниченным временем жизни особей. Модель представляет собой систему интегро-дифференциальных уравнений
![]()
с начальным условием
![]()
где ![]() , а оператор
, а оператор ![]() имеет вид
имеет вид ![]() ,
, ![]() .
.
В настоящей работе приводятся результаты изучения вопросов существования, единственности, неотрицательности и ограниченности решений системы уравнений (1) с начальным условием (2). Рассмотрены также достаточные условия экспоненциальной устойчивости нулевого решения, которые применяются к исследованию вопроса о вырождении популяций. Для изучения поведения решений используются принцип сжимающих отображений, монотонный метод [2, с. 43] и свойства М - матриц [3, с. 132].
2. Основные результатыВведем некоторые обозначения.Пусть ![]() - длина вектора
- длина вектора ![]() ,
, ![]() - норма матрицы A = ( ai j ), [4, с. 196], A+ - матрица, составленная из элементов
- норма матрицы A = ( ai j ), [4, с. 196], A+ - матрица, составленная из элементов ![]() , Rm+ - множество векторов
, Rm+ - множество векторов ![]() с неотрицательными компонентами. Если
с неотрицательными компонентами. Если ![]() , то запись u>0 означает, что ui>0 при всех
, то запись u>0 означает, что ui>0 при всех ![]() . Неравенства между векторами из Rm понимаются как неравенства между их комнонентами. Для фиксированного T>0 под C+T будем понимать пространство неотрицательных непрерывных на отрезке [0,T] функций
. Неравенства между векторами из Rm понимаются как неравенства между их комнонентами. Для фиксированного T>0 под C+T будем понимать пространство неотрицательных непрерывных на отрезке [0,T] функций ![]() с нормой
с нормой ![]() , где K>0 - некоторая константа, [2, с. 11]. В системе (1)
, где K>0 - некоторая константа, [2, с. 11]. В системе (1) ![]() , при
, при ![]() под
под ![]() понимается правосторонняя производная. Далее,
понимается правосторонняя производная. Далее, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Функции
. Функции ![]() предполагаются непрерывными в своих областях определения.
предполагаются непрерывными в своих областях определения.
От системы уравнений (1) с начальным условием (2) перейдем к эквивалентной системе интегральных уравнений вида
![]()
где (Fx)(t) =
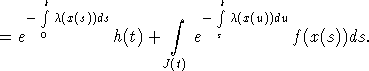
Здесь ![]() при
при ![]() , h(t) = 0 при
, h(t) = 0 при ![]() ,
, ![]() - отрезок интегрирования,
- отрезок интегрирования, ![]() . Примем в дальнейшем, что выполнено следующее предположение :
. Примем в дальнейшем, что выполнено следующее предположение :
H) элементы матрицы ![]() определены, непрерывны и ограничены,
определены, непрерывны и ограничены, ![]() ; функции
; функции ![]() удовлетворяют условию Липшица
удовлетворяют условию Липшица ![]() ,
, ![]() ,
, ![]() , где D - некоторое выпуклое подмножество Rm+.
, где D - некоторое выпуклое подмножество Rm+.
Пусть M1 и M2 такие постоянные, что ![]() ,
, ![]() ,
, ![]() . Зададим матрицы A,B,Q по формулам :
. Зададим матрицы A,B,Q по формулам : ![]() , где
, где ![]() при
при ![]() и
и ![]() при
при ![]() ,
, ![]() , Q = I - A B, I - единичная матрица. Положим
, Q = I - A B, I - единичная матрица. Положим
(Lx)(t) =
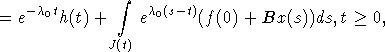
где ![]() . Тогда
. Тогда ![]() и для всех
и для всех ![]() таких, что
таких, что ![]() , верно неравенство
, верно неравенство ![]() .
.
Теорема 1. Пусть предположение H) выполняется на множестве D = Rm+. Тогда система уравнений (3) имеет единственное непрерывное решение x=x(t), определенное на ![]() , и справедливы оценки
, и справедливы оценки ![]() , где
, где ![]() .
.
Теорема 2. Пусть предположение H) выполняется на некотором прямоугольнике ![]() и существует
и существует ![]() , такой, что
, такой, что ![]() . Тогда система уравнений (3) имеет единственное непрерывное, ограниченное решение x=x(t), определенное на
. Тогда система уравнений (3) имеет единственное непрерывное, ограниченное решение x=x(t), определенное на ![]() , и справедливы оценки
, и справедливы оценки ![]() .
.
Теорема 3. Пусть предположение H) выполняется либо на множестве D = Rm+, либо на некотором прямоугольнике D = D0. Пусть, кроме того, f(0) = 0 и Q является невырожденной М - матрицей. Тогда система уравнений (1) имеет нулевое решение x(t) = 0, которое является экспоненциально устойчивым, иначе для всех ![]() верно
верно ![]() , где
, где ![]() .
.
Приведем краткую схему доказательства этих теорем. В условиях теоремы 1 будем искать функцию w(t), удовлетворяющую неравенствам ![]() . Выберем
. Выберем ![]() . Используя оценку
. Используя оценку ![]() , приходим к неравенству
, приходим к неравенству ![]() , где
, где ![]() ,
, ![]() . Имеем, что при
. Имеем, что при ![]()
![]() (поэлементно). Единичная матрица I является невырожденной М - матрицей. В силу непрерывной зависимости найдется такое a0>0, что (I - A0(a0) B) также будет невырожденной М - матрицей. Используя свойства невырожденных М - матриц, получаем, что существует
(поэлементно). Единичная матрица I является невырожденной М - матрицей. В силу непрерывной зависимости найдется такое a0>0, что (I - A0(a0) B) также будет невырожденной М - матрицей. Используя свойства невырожденных М - матриц, получаем, что существует ![]() , такой, что верно неравенство
, такой, что верно неравенство ![]() . Отсюда следует, что
. Отсюда следует, что ![]() при всех
при всех ![]() . Зафиксируем T>0 и обозначим через CwT множество всех функций
. Зафиксируем T>0 и обозначим через CwT множество всех функций ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() . Тогда из неравенств
. Тогда из неравенств ![]() следует, что
следует, что ![]() . Пусть множество
. Пусть множество ![]() . Для всех
. Для всех ![]() верно, что
верно, что ![]() , где
, где ![]() ,
, ![]() ,
, ![]() . Полагая
. Полагая ![]() , получаем, что отображение F является сжимающим. При доказательстве теоремы 2 функция w(t) ищется в виде w(t) = b0, где
, получаем, что отображение F является сжимающим. При доказательстве теоремы 2 функция w(t) ищется в виде w(t) = b0, где ![]() . Если существует
. Если существует ![]() , такой, что
, такой, что ![]() , то
, то ![]() и является сжимающим отображением на CwT. Используя далее принцип сжимающих отображений, убеждаемся в справедливости утверждений теорем 1 и 2.
и является сжимающим отображением на CwT. Используя далее принцип сжимающих отображений, убеждаемся в справедливости утверждений теорем 1 и 2.
Для доказательства теоремы 3 строится оценка на решение ![]() , где
, где ![]() , функция w(t) такова, что
, функция w(t) такова, что ![]() . Эти неравенства будут выполнены, если
. Эти неравенства будут выполнены, если ![]() , где
, где ![]() ,
, ![]() при
при ![]() при
при ![]() . Матрица (I - A1(a) B) непрерывно зависит от a и
. Матрица (I - A1(a) B) непрерывно зависит от a и ![]() (поэлементно) при
(поэлементно) при ![]() . Так как Q является невырожденной М - матрицей, то найдется a = a0 >0 такой, что (I - A1(a0) B) также будет невырожденной М - матрицей. Используя свойства невырожденных М - матриц, можно показать, что существуют
. Так как Q является невырожденной М - матрицей, то найдется a = a0 >0 такой, что (I - A1(a0) B) также будет невырожденной М - матрицей. Используя свойства невырожденных М - матриц, можно показать, что существуют ![]() и
и ![]() такие, что выполняется неравенство
такие, что выполняется неравенство ![]() . В итоге получаем, что справедливы оценки на решение
. В итоге получаем, что справедливы оценки на решение ![]() .
.
Установленные выше результаты указывают на корректность применения представленной модели в целях описания динамики численности популяций. Это связано с тем, что решения модели обладают такими важными свойствами, как существование, единственность, неотрицательность и ограниченность, которые соответствуют смыслу моделируемых процессов.
Важным следствием теоремы 3 являются достаточные условия, при которых популяция вырождается, т.е. ее численность x(t) такова, что ![]() при
при ![]() . Предположение H) задает ограничения на интенсивности процессов рождения и гибели особей, тогда как условие f(0) = 0 означает, что нет внешних источников поступления новых особей. Заметим, в частности, что предположение H) и условие f(0) = 0 выполняются для линейных процессов рождения и гибели особей. В нелинейном случае этому предположению и условию удовлетворяют f(x) и
. Предположение H) задает ограничения на интенсивности процессов рождения и гибели особей, тогда как условие f(0) = 0 означает, что нет внешних источников поступления новых особей. Заметим, в частности, что предположение H) и условие f(0) = 0 выполняются для линейных процессов рождения и гибели особей. В нелинейном случае этому предположению и условию удовлетворяют f(x) и ![]() , заданные в виде некоторых многочленов, рациональных функций либо функций с непрерывными частными производными. Функции такого вида широко используются в моделях биологических процессов, см., например, [5,6].
, заданные в виде некоторых многочленов, рациональных функций либо функций с непрерывными частными производными. Функции такого вида широко используются в моделях биологических процессов, см., например, [5,6].
Нетрудно показать, что матрица Q будет невырожденной М - матрицей для малых ![]() или при достаточно малых ненулевых элементах матрицы B. Если в условиях теоремы 3 D = Rm+, то экспоненциальная оценка на решение x(t) справедлива при любом начальном значении x(0). Если же D = D0, то эта оценка выполняется для x(0), лежащих в некоторой окрестности точки x = 0. В обоих случаях конкретный вид начального распределения особей по возрасту
или при достаточно малых ненулевых элементах матрицы B. Если в условиях теоремы 3 D = Rm+, то экспоненциальная оценка на решение x(t) справедлива при любом начальном значении x(0). Если же D = D0, то эта оценка выполняется для x(0), лежащих в некоторой окрестности точки x = 0. В обоих случаях конкретный вид начального распределения особей по возрасту ![]() не влияет на экспоненциальную оценку (вектор
не влияет на экспоненциальную оценку (вектор ![]() зависит только от значений x(0)). В рамках принятых предположений можно сделать следующий вывод: если в некоторых популяциях особи являются короткоживущими или интенсивности процесса рождения особей достаточно малы, то такие популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту.
зависит только от значений x(0)). В рамках принятых предположений можно сделать следующий вывод: если в некоторых популяциях особи являются короткоживущими или интенсивности процесса рождения особей достаточно малы, то такие популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту.
В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением
![]()
с начальным условием ![]() , где
, где ![]() , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни особей, то в соответствии с (1) следует рассмотреть уравнение
, см., например, [5, c. 14]. Если учитывать ограниченность времени жизни особей, то в соответствии с (1) следует рассмотреть уравнение
![]()
![]()
с начальным условием (2). Здесь в качестве множества D можно рассматривать произвольный отрезок [0, d], ![]() . Пусть
. Пусть ![]() . Из теоремы 3 следует, что решение x(t) данного интегро-дифференциального уравнения таково, что
. Из теоремы 3 следует, что решение x(t) данного интегро-дифференциального уравнения таково, что ![]() при
при ![]() для любых начальных значений x(0). Можно показать, что этот результат справедлив и для
для любых начальных значений x(0). Можно показать, что этот результат справедлив и для ![]() . Неравенства
. Неравенства ![]() задают на плоскости
задают на плоскости ![]() область параметров, при которых популяция вырождается. Кроме того, можно показать, что для
область параметров, при которых популяция вырождается. Кроме того, можно показать, что для ![]() решение
решение ![]() при
при ![]() , независимо от значений x(0), где x* - единственный положительный корень уравнения
, независимо от значений x(0), где x* - единственный положительный корень уравнения ![]() С ростом t решение x(t) приближается к x* либо монотонно, либо с затухающими колебаниями. Отметим, что решение логистической модели таких колебаний не имеет.
С ростом t решение x(t) приближается к x* либо монотонно, либо с затухающими колебаниями. Отметим, что решение логистической модели таких колебаний не имеет.
В заключение укажем, что система уравнений (1) с начальным условием (2) является обобщением некоторых из моделей, рассмотренных в работе [7].
Список литературыПерцев Н.В. Применение одного дифференциального уравнения с последействием в моделях динамики популяций // Фундаментальная и прикладная математика / Ред. А.К. Гуц. Омск, 1994. С.119 - 129.
Красносельский М.А. и др. Приближенное решение операторных уравнений. М.: Наука, 1969.
Berman A., Plemmous R.J. Nonnegative Matrices in the Mathematical Sciences. New York, Academic Press, 1979.
Беллман Р. Введение в теорию матриц. М.: Наука, 1976.
Свирежев Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М.: Наука, 1987.
Марри Дж. Нелинейные дифференциальные уравнения в биологии. Лекции о моделях. М.: Мир, 1983.
Cooke K., Yorke A. Some equations Modelling Growth Processes and Gonorhea Epidemics // Math. Biosci., 1973. V.16. P.75 - 1
Похожие работы
... сигналов, передающихся от одного живого организма другому (от родителей - потомкам) или от одних клеток, тканей, органов другим в процессе развития особи; 6. в математике, кибернетике – количественная мера устранения энтропии (неопределенности), мера организации системы; 7. в философии – свойство материальных объектов и процессов сохранять и порождать определенное состояние, которое в ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... республиканского бюджета, которое является защищенной статьей текущих расходов бюджетной классификации. Направления использования средств, предусмотренных в республиканском бюджете, определяются законодательством Республики Беларусь. Порядок финансирования научной, научно-технической и инновационной деятельности за счет средств республиканского бюджета устанавливается Правительством Республики ...







0 комментариев