Обработка результатов многократных и косвенных измерений

6. Обработка результатов многократных и косвенных измерений

Качество измерений характеризуются рядом показателей.

Сходимость результатов измерений – близость друг к другу результатов измерений, выполненных повторно в тех же условиях.

Воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разное время, в разных местах, разными операторами и средствами.

Точность измерений – близость результата измерений к истинному значению измеряемой величины.

Правильность измерений – близость к нулю систематической погрешности измерений.

Достоверность измерений – близость к нулю случайной или отнесенной к случайной неисключенной систематической погрешности. Достоверность измерений характеризуется доверительной вероятностью того, что истинное значение лежит в указанных доверительных границах:

Рд = Р{(х – tσ) ≤ Х ≤ (х + tσ)}.

Возможность повышения достоверности результатов измерений обеспечивается при проведении многократных измерений. Результат многократных измерений определяется как параметр положения центра распределения полученных данных (Хц). Преимущество и основной смысл многократных измерений заключается в том, что координата центра распределения совокупности результатов измерений одного и того же значения физической величины имеет меньшую полосу неопределенности, чем каждый отдельно взятый результат однократного измерения. Существуют соотношения: D(Хц) = D(х_i)/n и σ(Хц) = σ(х_i)/, где n – число измерений.

Последовательность обработки результатов многократных измерений следующая:

- исправление результатов наблюдений, если это возможно (внесение поправок);

- вычисление оценки параметра положения центра выборки Хц (среднее арифметическое, медиана или другая оценка);

- вычисление выборочного СКО оценки параметра положения центра по формуле

σ(Хц) =

- определение границ доверительного интервала для случайной погрешности

∆_сл= ±t_pnσ(Хц).

Следует помнить, что при многократных измерениях уменьшаются только случайные погрешности, а систематические остаются без изменения и должны суммироваться со случайными. Следующие этапы обработки данных:

- сравнение ∆_сл с неисключенными систематическими составляющими погрешности измерений и выявление значимых составляющих;

- суммирование неисключенных систематических погрешностей

Δ _СΣ = К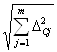 

- определение суммарной погрешности Δ _Σ =.

Результат измерений записывается в виде Хц± Δ _Σ, Рд.

Пример. При многократном измерении тока получены значения в мА: 98, 100, 97, 101, 99, 102, 103. Определить доверительные границы для истинного значения измеряемой величины с вероятностью Р = 0,95 (t_p= 2,45).

Параметр положения центра выборки Хц (среднее арифметическое) Хц =100 мА.

СКО оценки параметра положения центра

σ(Хц) = =

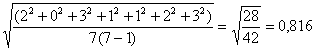
Границы доверительного интервала для случайной погрешности

∆_сл= ±t_pσ(Хц) = ±(2,45∙0,816) ≈ ±2 мА.

Результат измерений: 100±2 мА, Р = 0,95.

Результат косвенного измерения определяется расчетом по известной функции Ζ = f(х₁, х₂, …) и измеренным значениям аргументов х_i. Так как каждое значение х_i измерено с погрешностью, задача расчета погрешности результата измерений сводится также к суммированию погрешностей измерения аргументов. Отличие косвенных измерений состоит в том, что в зависимости от вида функции вклад отдельных аргументов в результат и его погрешность может быть различным. Поэтому при расчете погрешности результата косвенных измерений вводятся коэффициенты влияния аргументов на результат измерений, представляющие собой частные производные функции по соответствующим аргументам:

Δ(Ζ) =(∂f/∂х_i)Δ(х_i).

Для дисперсий:

σ²(Ζ) = (∂f/∂х_i)² σ²(х_i).

Метод частных производных правомерен для суммирования абсолютных погрешностей линейных функций, в которые аргументы входят в первой степени и коэффициенты влияния ∂f/∂х_i не зависят от аргументов. Для нелинейных функций проводится сначала логарифмирование (или другая операция линеаризации функции, в общем случае – разложение в ряд Тейлора), затем дифференцирование.

Пусть Ζ = ∏( хª₁, хⁿ₂, …).

Логарифмирование: lnΖ = alnх₁ +nlnх₂, …

Дифференцирование: dΖ/Ζ = a(dх₁/х₁)+ n(dх₂/х₂) +…, после чего, перейдя к малым приращениям (погрешностям), получим формулу расчета относительных погрешностей: δ(Ζ) = a δ(х₁) + n δ(х₂) +…

Для дисперсий: σ²( δ _Ζ) = b_j² σ²( δ_хj).

Итак, расчет погрешности косвенного измерения проводится в два этапа: 1) вывод формулы для расчета абсолютной погрешности (дифференцирование) или относительной погрешности (логарифмирование + дифференцирование) в зависимости от вида функции связи измеряемых величин; 2)расчет погрешности в соответствии с полученной формулой по правилам суммирования составляющих. При этом, если составляющие погрешности рассматриваются как случайные величины, знаки, полученные при дифференцировании, не учитываются.

Пример. Оценить значение и погрешность измерения мощности, поглощаемой на сопротивлении R = 100 Ом при напряжении U = 10 В. СКО относительных погрешностей измерений напряжения и сопротивления составляют: σ(δ_U) = 0,5%, σ(δ_R) = 1%.

Поглощаемая мощность W = U²/ R = 1Вт.

Для оценки погрешности измерения проведем линеаризацию функции:

lnW = 2lnU- lnR.

Тогда относительная погрешность измерения мощности δ_W= 2δ_U+δ_R, а дисперсия относительной погрешности: σ²(δ_W) = 4 σ² (δ_U)+σ² (δ_R)

СКО относительной погрешности σ(δ_W) = ≈ 1,414%

Приняв доверительную вероятность Р=0,9 (t_p=1,6), запишем результат измерений:

W = 1 Вт; δ = ±2,3%, Р = 0,9.

Похожие работы

Метрология и ее разделы

Скачать

147234

13

2

... приемлемые для широких кругов термины с описанием выражаемых ими понятий. Словарь содержит шесть разделов: Величины и единицы; Измерения; Результаты измерений; Средства измерений; Характеристика средств измерений; Эталоны. Кроме этого общего словаря, издается Словарь по законодательной метрологии, в котором освещается деятельность государственных метрологических служб в различных странах мира. ...

Метрологическое обеспечение деятельности по стандартизации в РФ

Скачать

19158

0

0

... . 3.    Проблемы в системе метрологического обеспечения деятельности по стандартизации и сертификации Важное влияние на развитие системы метрологического обеспечения деятельности по стандартизации и сертификации в РФ оказывает несовершенство нормативной и методической базы. В частности, царит неразбериха и путаница с самым главным понятием – «испытание». Как отметил генеральный директор ...

Метрологическое обеспечение измерений

Скачать

17339

0

1

ведении находятся стандарты, эталоны, метрическая система и система исчисления времени. Под метрологическим обеспечением измерений понимается деятельность метрологических и других служб, направленная: - на создание в стране необходимых эталонов, образцовых и рабочих средств измерений; - на их правильный выбор и применение; - на разработку и применение метрологических правил и норм; - на ...

Метрологическое обеспечение в сфере здравоохранения

Скачать

32023

0

0

... к средствам измерений обязывает метрологическую службу постоянно увеличивать перечень обслуживаемых средств измерений, из-за чего увеличивается объем работы метрологических служб в области обеспечения единства измерений в сфере здравоохранения. Возникает необходимость расширения подразделений, ответственных за проведение организационно-методических работ по обеспечению единства и достоверности ...