Механизмы компрессора

КУРСОВОЙ ПРОЕКТ

на тему: «Механизмы компрессора»

 

1. Структурный анализ механизмов

  1.1 Структурный анализ рычажного механизма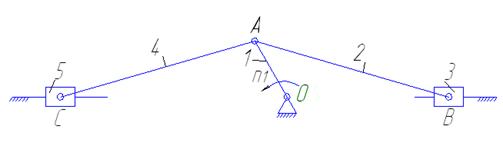

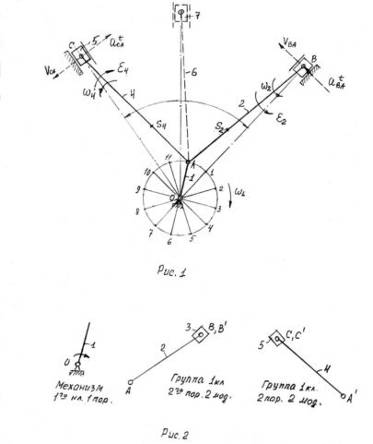
Рисунок 1.1. Подвижные звенья механизма

1-кривошип

2-шатун

3-ползун

4-шатун

5-ползун

Кинематические пары.

О (0-1),вр.,5 кл.

А (1-4),вр.,5 кл.

А'(1-2),вр.,5 кл.

В (2-3),вр.,5 кл.

В'(3-0),пост.,5 кл.

С (4-5),вр.,5 кл.

С'(5-0),пост.,5 кл.

Найдём число степеней свободы.

Запишем формулу Чебышева.

W=3∙n-2∙P₅-P₄ (1.1)

Где, W-число степеней свободы,

n-число подвижных звеньев,

P₄ - число пар 4-го класса,

P₅ - число пар 5-го класса.

W=3∙5-2∙7=1

Число степеней свободы рычажного механизма равно 1.

Разобьём механизм на группы Асура и рассмотрим каждую группу в отдельности.

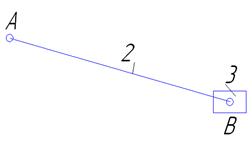Группа 2-3 (Рисунок 1.2)

A'(1-2)-внешняя

B'(3-0)-внешняя

B (2-3)-внутренняя

W=3∙2-2∙3=0

II кл. 2 вид Рисунок 1.2

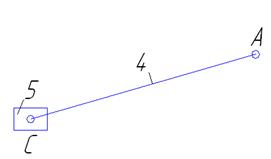Группа 4-5 (Рисунок 1.3)

А (1-4)-внешняя

С' (5-0)-внешняя

C (4-5)-внутренняя

W=3∙2-2∙3=0

II кл. 2 вид

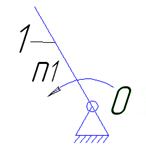
O (0-1)

W=3-2=1

Рисунок 1.4

Составим структурную формулу:

Механизм является механизмом 2кл.,2в..

1.2 Структурный анализ зубчатого механизма

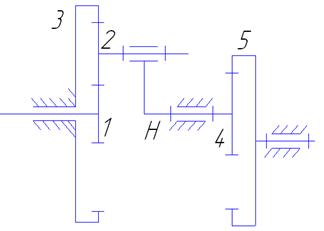
Рисунок 1.5. Подвижные звенья механизма

1 – центральное колесо

2 – сателлит

3 – зубчатое колесо

H – водило

4 – зубчатое колесо

5 – зубчатое колесо

Кинематические пары.

(1-0),вр.,5 кл.

(5-0),вр.,5 кл.

(2-H),вр.,5 кл.

(4-0),вр.,5 кл.

(1-2),вр.,4 кл.

(2-3),вр.,4 кл.

(4-5),вр.,4 кл.

Найдём число степеней свободы.

Исходя из формулы Чебышева имеем,

W=3∙4-2∙4-3=1

Число степеней свободы зубчатого механизма равно 1, следовательно, данный механизм является планетарным.

  1.3 Структурный анализ кулачкового механизма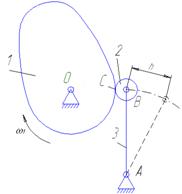

Рисунок 1.6. Подвижные звенья механизма

1-кулачок

2-ролик

3-коромысло

Кинематические пары.

О (1-0),вр.,5 кл.

А (3-0),вр.,5 кл.

В (2-3),вр.,5 кл.

С (1-2),пост.,4 кл.

Найдём число степеней свободы.

W=3∙n-2∙P₅-P₄

W=3∙3-2∙3-1=2

Число степеней свободы равно 2.

Так как W≠1, то присутствует лишнее звено - ролик.

2. Динамический анализ рычажного механизма

  2.1 Определение скоростей

Для заданной схемы механизма строим 12 положений.

Определяем масштабный коэффициент построения механизма:

(2.1)

где, - масштабный коэффициент,

 - длина звена,

 - длина звена на чертеже,

Запишем длинны звеньев механизма на чертеже

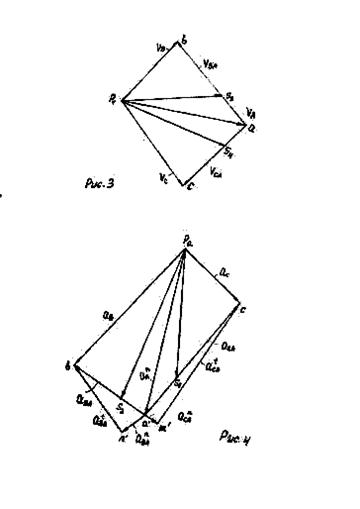
Приступаем к построению повёрнутых планов скоростей для каждого положения. Рассмотрим пример построения для положения №5:

У кривошипа определяем скорость точки А

 (2.2)

где,  - длина звена,

 - угловая скорость кривошипа,

Для построения вектора скорости точки А определяем масштабный коэффициент

 (2.3)

где,  - скорость точки А,

 - вектор скорости точки А,

 - полюс, выбираемый произвольно

Для определения скорости точки B запишем систему уравнений:

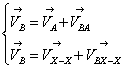(2.4)

 - из задания

Для определения скорости центра масс 2-го звена S₂ воспользуемся соотношением:

(2.5)

где, , - расстояния между соответствующими точками на механизме, м

,  - длинны векторов скоростей на плане, мм

 мм

Соединив, точку  и π получим скорость центра масс второго звена.

Для определения скорости точки C запишем систему уравнениё:

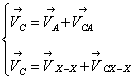(2.6)

 - из задания

Для определения скорости центра масс 4-го звена S₄ воспользуемся соотношением:

(2.7)

где, , - расстояния между соответствующими точками на механизме, м

,  - длинны векторов скоростей на плане, мм

 мм

Соединив, точку  и π получим скорость центра масс второго звена.

Определим значения угловых скоростей звеньев.

Направление  определяем, перенеся вектор ab в точку S₂ – второе звено вращается против часовой стрелки. Аналогично получим, что  направлена по часовой стрелке.

Скорости точек остальных положений определяются аналогичным образом. Все значения сводим в таблицу(2.1).

Таблица 2.1 – Значения линейных и угловых скоростей

N положения	VB=VS3,	VS2,	VС=VS5,	VS4,	VBA= VCA,	=,
1	0	5,58	0	5,58	8,37	33,48
2	5,36	6,66	3,01	6,14	7,34	29,37
3	8,46	8,14	6,04	7,39	4,36	17,42
4	8,37	8,37	8,37	8,37	0	0
5	6,04	7,39	8,46	8,14	4,36	17,42
6	3,01	6,14	5,36	6,66	7,34	29,37
7	0	5,58	0	5,58	8,37	33,48
8	3,01	6,14	5,36	6,66	7,34	29,37
9	6,04	7,39	8,46	8,14	4,36	17,42
10	8,37	8,37	8,37	8,37	0	0
11	8,46	8,14	6,04	7,39	4,36	17,42
12	5,36	6,66	3,01	6,14	7,34	29,37

2.2 Определение приведённого момента инерции звеньев

Приведённый момент инерции определяется по формуле:

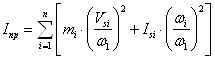(2.8)

где,  - масса i-го звена рычажного механизма, кг

 - линейная скорость центра масс i-го звена,

 - угловая скорость i-го звена,

 - приведённый момент инерции i-го звена по отношению к центру масс

(2.9)

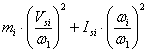 - для звена, совершающего сложное движение

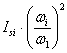 - для звена, совершающего вращательное или колебательное движения

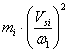 - для звена, совершающего поступательное движение

Запишем формулу для нашего механизма:

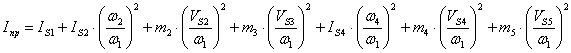(2.10)

Для 5-го положения приведём расчёт, а для остальных положений сведём значение в таблицу 2.2

 кг∙м²

 кг∙м²

 кг∙м²

Записав формулу (2.11) для положения №5 и подставив известные величины, получим:

 

Таблица 2.2 – Приведённые моменты инерции

N положения	, кг∙м2	N положения	, кг∙м2
1	0,0592	7	0,0592
2	0,0886	8	0,0886
3	0,1441	9	0,1441
4	0,1701	10	0,1701
5	0,1441	11	0,1441
6	0,0886	12	0,0886

Для построения графика приведённого момента инерции необходимо Рассчитать масштабные коэффициенты.

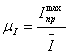, (2.11)

где,  - масштабный коэффициент по оси

 - максимальное значение , кг∙м²

 - значение  на графике, мм

, (2.12)

где,  - масштабный коэффициент по оси φ

 - принятая длинна одного оборота по оси φ

 

2.3 Определение приведённого момента сопротивления

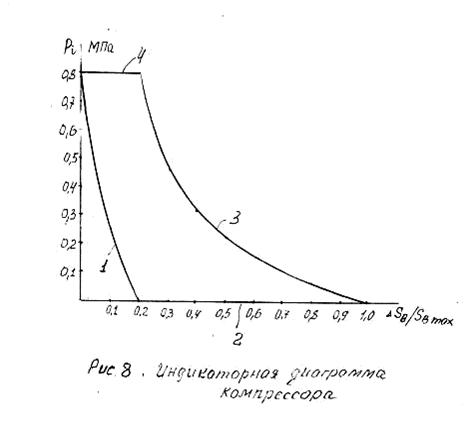
Определим максимальную силу, которая действует на ползун В по следующей формуле:

 (2.13)

где, - Максимальное индикаторное давление,

 - диаметр поршня,

Определим расстояние от оси  до графика по формуле (2.14)

На планах скоростей прикладываем все силы, действующие на механизм, и указываем их плечи. Составляем сумму моментов относительно полюса и решаем уравнение.

Для 1-го положения:

  (2.14)

где,  плечи соответствующих сил, снятые с плана скоростей, мм.

H,

, во всех положениях

H

Находим момент привидения:

 (2.15)

где,  - приведённая сила, Н

 - длина соответствующего звена, м

 Н∙м

Для 2-го положения:

  

H

 Н∙м

Для 3-го положения:

  

H

 Н∙м

Для 4-го положения:

  

H

 Н∙м

Для 5-го положения:

  

H

 Н∙м

Для 6-го положения:

  

H

 Н∙м

Для 7-го положения:

  

H

 Н∙м

Для 8-го положения:

  

H

 Н∙м

Для 9-го положения:

  

H

 Н∙м

Для 10-го положения:

  

H

 Н∙м

Для 11-го положения:

  

H

 Н∙м

Для 12-го положения:

 

H

 Н∙м

Все значения сводим в таблицу.

Таблица 2.4 – Приведённые моменты сопротивления

N положения	,	N положения	,
1	8,88	7	8,88
2	650,08	8	634,72
3	180,7	9	171,81
4	681,01	10	681,01
5	1665,43	11	1674,32
6	1242,3	12	1257,69

Определяем масштабный коэффициент построения графика моментов сопротивления:

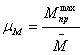, (2.16)

где,  - масштабный коэффициент по оси

 - максимальное значение ,

 - значение  на графике, мм

По данным расчёта строится график .

Путём графического интегрирования графика приведённого момента строится график работ сил сопротивления .

График работ движущих сил  получаем в виде прямой, соединяющей начало и конец графика работ сил сопротивления.

Масштабный коэффициент графика работ:

, (2.17)

где, Н – полюсное расстояние для графического интегрирования, мм

Н=60мм

Момент движущий  является величиной постоянной и определяется графически.

Путём вычитания ординат графика  из соответствующих ординат  строится график изменения кинетической энергии .

(2.18)

По методу Ф. Витенбауэра на основании ранее построенных графиков и  строим диаграмму энергия-масса .

Определяем углы и  под которыми к диаграмме энергия-масса, проводятся касательные.

(2.19)

 (2.20)

где,  - коэффициент неравномерности вращения кривошипа.

Из чертежа определим

 

Определяем момент инерции маховика

,  (2.21)

Маховик устанавливается на валу звена приведения.

Определим основные параметры маховика.

,кг (2,22)

где,  - масса маховика, кг

 - плотность материала,  (материал-Сталь 45)

 - ширина маховика, м

 - диаметр маховика, м

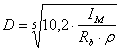,м  (2,23)

где,  - коэффициент (0,1÷0,3),

м

м

кг