Навигация
Силовой анализ рычажного механизма
3. Силовой анализ рычажного механизма
3.1 Построение плана скоростей для расчётного положенияРасчётным положением является положение №11. Построение плана скоростей описано в разделе №2. Масштабный коэффициент плана скоростей
![]()
![]()
Определяем угловое ускорение звена 1.
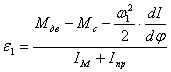 , (3.1)
, (3.1)
где, ![]() - момент от сил движущих,
- момент от сил движущих, ![]()
![]() - момент от сил сопротивления,
- момент от сил сопротивления, ![]()
![]() - приведённый момент инерции маховика,
- приведённый момент инерции маховика, ![]()
![]() - приведённый момент инерции рычажного механизма для расчётного положения,
- приведённый момент инерции рычажного механизма для расчётного положения, ![]()
![]() - первая производная от приведённого момента инерции механизма для расчётного положения
- первая производная от приведённого момента инерции механизма для расчётного положения
![]() , (3.2)
, (3.2)
где, ![]() - масштабный коэффициент по оси
- масштабный коэффициент по оси ![]() ,
, ![]()
![]() - масштабный коэффициент по оси φ,
- масштабный коэффициент по оси φ, ![]()
![]() - угол между касательной, проведённой к кривой графика
- угол между касательной, проведённой к кривой графика ![]() в расчётном положении и осью φ.
в расчётном положении и осью φ. ![]()
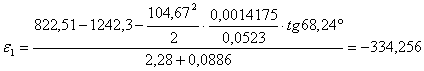
![]()
Знак минуса говорит о том, что кривошип ОА замедляется. Направляем ![]() против направления
против направления ![]() и берём значение ускорения по модулю.
и берём значение ускорения по модулю.
Строим план ускорений для расчётного положения.
Скорость точки А определяем по формуле
![]() , (3.3)
, (3.3)
где, ![]() - ускорение точки А,
- ускорение точки А, ![]()
![]() - нормальное ускорение точки А относительно точки О,
- нормальное ускорение точки А относительно точки О, ![]()
![]() - тангенциальное (касательное) ускорение точки А,
- тангенциальное (касательное) ускорение точки А, ![]()
Ускорение ![]() найдём по формуле:
найдём по формуле:
![]() , (3.4)
, (3.4)
где, ![]() - угловая скорость кривошипа,
- угловая скорость кривошипа, ![]()
![]() - длина звена ОА, м
- длина звена ОА, м
![]()
![]()
Ускорение ![]() найдём по формуле:
найдём по формуле:
![]() , (3.5)
, (3.5)
![]()
![]()
Из произвольно выбранного полюса ![]() откладываем вектор
откладываем вектор ![]() длиной 100 мм. Найдём масштабный коэффициент плана скоростей.
длиной 100 мм. Найдём масштабный коэффициент плана скоростей.
![]() , (3.6)
, (3.6)
![]()
![]()
Определим длину вектора ![]() :
:
![]()
Ускорение точки А определим из следующеё формулы:
![]()
![]()
Определим ускорение точки B из следующей системы уравнений:
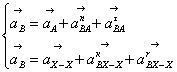 , (3.7)
, (3.7)
Для определения нормальных ускорений точки В относительно точек А и С
Воспользуемся следующими формулами:
![]()
![]()
Определим длину векторов ![]() :
:
![]()
![]()
Ускорение направляющей ![]() равно нулю, т.к. она неподвижна.
равно нулю, т.к. она неподвижна.
Кореолисово ускорение точки В относительно направляющей![]() рано нулю, т.к. точка В движется только поступательно относительно
рано нулю, т.к. точка В движется только поступательно относительно ![]() .
.
Ускорение точки В найдём, решив системе (3.7) векторным способом:
Из вершины вектора ускорения точки А (![]() ) откладываем вектор
) откладываем вектор ![]() (параллелен звену АВ и направлен от В к А), из вершины вектора
(параллелен звену АВ и направлен от В к А), из вершины вектора ![]()
проводим прямую перпендикулярную звену АВ (линия действия ![]() ); из полюса
); из полюса ![]() проводим горизонтальную прямую (линия действия
проводим горизонтальную прямую (линия действия ![]() ); на пересечении линий действия векторов
); на пересечении линий действия векторов ![]() и
и ![]() получим точку b, соединив полученную точку с полюсом, получим вектор ускорения точки В.
получим точку b, соединив полученную точку с полюсом, получим вектор ускорения точки В.
Из плана ускорений определяем вектор ускорения точки В и вектор тангенциального ускорения ![]() :
:
![]()
![]()
![]()
![]()
Ускорение сочки С определяем аналогично ускорению точки B.
![]()
![]()
Определим длину векторов ![]() :
:
![]()
![]()
![]()
![]()
![]()
Из полученных тангенциальных ускорений найдём угловые ускорения 2-го и 3-го звеньев:
![]()
![]()
Определим ускорения центров масс звеньев:
Ускорение центра масс 2-го звена ![]() найдём из соотношения (3.10)
найдём из соотношения (3.10)
![]() (3.8)
(3.8)
Из плана ускорений ![]() мм
мм
![]() мм
мм
![]() мм
мм
![]()
![]()
Ускорение центра масс 4-го звена ![]() найдём из соотношения (3.11)
найдём из соотношения (3.11)
![]() (3.9)
(3.9)
Из плана ускорений ![]() мм
мм
![]() мм
мм
![]() мм
мм
![]()
![]()
Ускорения центров масс 3-го и 5-го звеньев равны ускорениям точек D и D’ соответственно:
![]()
![]()
![]()
![]()
Значения всех ускорений сведём в таблицу:
Таблица 3.1 – Ускорения звеньев
| Ускорение точек механизма | Значение, | Ускорение центров масс и угловые ускорения | значение, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --- | --- |
|
|
| --- | --- |
Силы инерции определяем по формуле:
![]() (3.10)
(3.10)
где. ![]() - масса i-го звена, кг;
- масса i-го звена, кг;
![]() - ускорение центра масс i-го звена,
- ускорение центра масс i-го звена, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определяем моменты инерции звеньев:
![]() (3.11)
(3.11)
где, ![]() - момент инерции i-го звена,
- момент инерции i-го звена, ![]()
![]() - момент инерции i-го звена относительно центра масс,
- момент инерции i-го звена относительно центра масс, ![]()
![]() - угловая скорость i-го звена,
- угловая скорость i-го звена, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассчитаем силу тяжести каждого звена:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
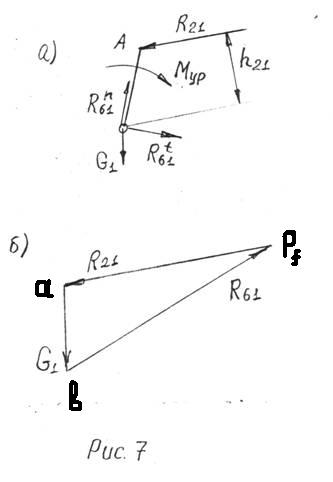
Рассмотрим группу Асура 2-3:
Найдём тангенциальную реакцию из следующего уравнения:
 (3.12)
(3.12)
Из уравнения (3.12) получим
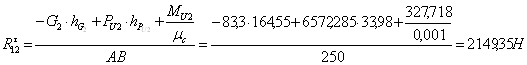
С помощью плана сил определим неизвестные реакции ![]() и
и ![]() :
:
![]()
Найдём масштабный коэффициент
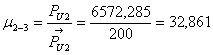
![]()
Из плана сил определяем значения неизвестных сил:
![]()
![]()
![]()
![]()
Реакцию ![]() определяем из следующего векторного уравнения
определяем из следующего векторного уравнения
![]()
![]()
![]()
![]() найдём из векторного уравнения
найдём из векторного уравнения
![]() , отсюда
, отсюда ![]()
![]()
Таблица 3.3 – Силы и вектора сил 2-го и 3-го звеньев
|
|
|
|
|
|
|
|
|
| |
|
| 9196,598 | 2149,35 | 9444,472 | 6572,285 | 83,3 | 384,65 | 47,04 | 2981,904 | 1370,979 |
|
| 279,86 | 65,4 | 287,4 | 200 | 2,53 | 11,7 | 1,43 | 90,74 | 41,72 |
Рассмотрим группу Асура 4-5:
Найдём тангенциальную реакцию из следующего уравнения:
![]() (3.13)
(3.13)
Из уравнения (3.13) получим
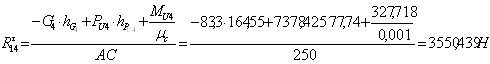
С помощью плана сил определим неизвестные реакции ![]() и
и ![]() :
:
![]()
Найдём масштабный коэффициент

![]()
Из плана сил определяем значения неизвестных сил:
![]()
![]()
![]()
![]()
Реакцию ![]() определяем из следующего векторного уравнения
определяем из следующего векторного уравнения
![]()
![]()
![]()
![]() найдём из векторного уравнения
найдём из векторного уравнения
![]() , отсюда
, отсюда ![]()
![]()
Таблица 3.3 – Силы и вектора сил 2-го и 3-го звеньев.
|
|
|
|
|
|
|
|
|
| |
|
| 13499,197 | 3550,439 | 13958,357 | 7378,425 | 83,3 | 24183,7 | 47,04 | 4432,944 | 3459,338 |
|
| 365,91 | 96,24 | 378,356 | 200 | 2,25 | 655,524 | 1,27 | 120,159 | 93,769 |
Рассмотрим начальный механизм.
Определим уравновешивающую силу ![]()


![]()
Уравновешивающий момент равен
![]()
![]()
Реакцию ![]() определяем графически
определяем графически
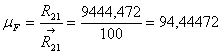
![]()
![]()
Из плана сил находим
![]()
![]()
3.5 Определение уравновешивающей силы методом Жуковского
Для этого к повёрнутому на ![]() плану скоростей в соответствующих точках прикладываем все внешние силы действующие на механизм, не изменяя их направления. Моменты раскладываем на пару сил, изменив их направления.
плану скоростей в соответствующих точках прикладываем все внешние силы действующие на механизм, не изменяя их направления. Моменты раскладываем на пару сил, изменив их направления.
![]() , (3.14)
, (3.14)
где, ![]() и
и ![]() - пара сил,
- пара сил, ![]()
![]() - момент инерции i-го звена,
- момент инерции i-го звена, ![]()
![]() - длина i-го звена,
- длина i-го звена, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Записываем уравнение моментов сил относительно полюса ![]() :
:
![]() , отсюда
, отсюда


Уравновешивающий момент равен
![]()
![]()
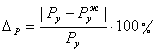 , (3.15)
, (3.15)
где, ![]() - сила полученная методом Жуковского,
- сила полученная методом Жуковского, ![]()
![]() - сила полученная методом планов,
- сила полученная методом планов, ![]()
![]() - погрешность,
- погрешность, ![]()
![]()
4. Проектирование кинематической схемы планетарного редуктора и расчёт эвольвентного зацепления 4.1 подбор числа зубьев и числа сателлитов планетарного редуктора
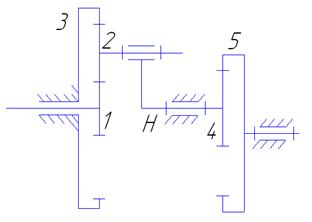
Рисунок 4.1
Определим неизвестное число зубьев 3-го колеса из условия соосности:
![]() (4.1)
(4.1)
где, ![]() - число зубьев 1-го колеса
- число зубьев 1-го колеса
![]() - число зубьев 2-го колеса
- число зубьев 2-го колеса
![]()
Определим передаточное отношение ![]()
![]() (4.2)
(4.2)
где, ![]() - передаточное отношение от 1-го звена к водилу, при неподвижном третьем звене
- передаточное отношение от 1-го звена к водилу, при неподвижном третьем звене
![]() - передаточное отношение от 4-го звена к пятому
- передаточное отношение от 4-го звена к пятому
![]() (4.3)
(4.3)
где, ![]() - число зубьев 4-го колеса
- число зубьев 4-го колеса
![]() - число зубьев 5-го колеса
- число зубьев 5-го колеса
![]()
![]() (4.4)
(4.4)
где, ![]() - передаточное число от 1-го ко 3-му колесу при неподвижном водиле
- передаточное число от 1-го ко 3-му колесу при неподвижном водиле
![]() (4.5)
(4.5)
где, ![]() - передаточное число от 1-го ко 2-му колесу
- передаточное число от 1-го ко 2-му колесу
![]() - передаточное число от 2-го ко 3-му колесу
- передаточное число от 2-го ко 3-му колесу
![]()
![]()
![]()
Проверяем условие соседства:
![]() (4.6)
(4.6)
где, ![]() - число сателлитов планетарного механизма
- число сателлитов планетарного механизма
Из формулы (4.4) выразим K
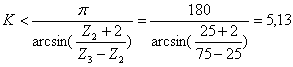
Примем ![]()
![]()
![]()
![]() - условие соседства выполняется
- условие соседства выполняется
Проверяем условие сборки
![]() (4.7)
(4.7)
где, ![]() - сумма чисел зубьев в одной из ступеней механизма
- сумма чисел зубьев в одной из ступеней механизма
![]() - целое число
- целое число
![]() - условие сборки выполняется
- условие сборки выполняется
Рассчитаем радиусы колёс
![]() (4.8)
(4.8)
где, ![]() - радиус колеса,
- радиус колеса, ![]()
![]() - модуль
- модуль
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Изображаем механизм в выбранном масштабе
![]()
![]() (4.9)
(4.9)
Определим радиусы колёс на схеме
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Строим план линейных скоростей. Для построения прямой распределения скоростей точек звена необходимо знать скорости двух точек. Для 1-го звена это точки А и О. Скорость точки О равна нулю, так как ось неподвижна. Скорость точки А определим по формуле
![]() (4.10)
(4.10)
где, ![]() - угловая скорость 1-го звена,
- угловая скорость 1-го звена, ![]()
Угловую скорость 1-го звена определим по формуле
![]() (4.11)
(4.11)
где, ![]() - частота вращения двигателя,
- частота вращения двигателя, ![]()
![]()
![]()
![]()
![]()
Определим угловую скорость вращения водила и второго зубчатого колеса
![]()
![]()
![]()
![]()
Вектор скорости точки А ![]() изображаем в виде отрезка Aa. Принимаем
изображаем в виде отрезка Aa. Принимаем ![]() .
.
Определим масштабный коэффициент
![]() (4.12)
(4.12)
где, ![]() - масштабный коэффициент скорости,
- масштабный коэффициент скорости, ![]()
![]()
![]()
Прямая Оа является линией распределения скоростей точек 1-го звена.
Скорость точки В равна нулю, так как колесо 3 неподвижно.
Прямая Оb является линией распределения скоростей тачек водила.
Строим план угловых скоростей.
Из произвольно выбранной точки Р строим пучок лучей, параллельных прямым Оа, Оb и Eb. При пересечении этих прямых с горизонтальной осью расположенной от точки Р на произвольном расстоянии РS, получим отрезки S1, S5 и SH, которые являются аналогами угловых скоростей.
Найдём передаточное отношение
![]() (4.13)
(4.13)
![]()
Рассчитаем погрешность двух методов
![]() (4.14)
(4.14)
где, ![]() - передаточное отношение, заданное в условии
- передаточное отношение, заданное в условии
![]() - передаточное отношение найденное с помощью плана угловых скоростей
- передаточное отношение найденное с помощью плана угловых скоростей
![]()
Рассчитываем смещение колёс
Так как ![]() , то
, то ![]()
Так как ![]() , то
, то ![]()
Коэффициент суммы смещений
![]() (4.15)
(4.15)
где, ![]() - смещение 1-го колеса
- смещение 1-го колеса
![]() - смещение 2-го колеса
- смещение 2-го колеса
![]()
Определим угол зацепления по формуле
![]() (4.16)
(4.16)
где, ![]() ,
, ![]() - эвольвентная функция углов
- эвольвентная функция углов ![]() и
и ![]()
![]()
![]()
Межосевое расстояние определим по формуле
![]() (4.17)
(4.17)
где, ![]() - модуль зубчатой передачи
- модуль зубчатой передачи
![]()
![]()
Определим делительные диаметры
![]() (4.18)
(4.18)
![]()
![]()
![]()
![]()
Делительное межосевое расстояние
![]() (4.19)
(4.19)
![]()
![]()
Коэффициент воспринимаемости смещения
![]() (4.20)
(4.20)
где, ![]() - межосевое расстояние,
- межосевое расстояние, ![]()
![]() - делительное межосевое расстояние,
- делительное межосевое расстояние, ![]()
![]()
Коэффициент уравнительного смещения
![]() (4.21)
(4.21)
![]()
Определим радиусы начальных окружностей
![]() (4.22)
(4.22)
![]()
![]()
![]()
![]()
Радиусы вершин зубьев
![]() (4.23)
(4.23)
где, ![]() - коэффициент высоты головки зуба
- коэффициент высоты головки зуба
![]()
![]()
![]()
![]()
Радиусы впадин зубьев
![]() (4.24)
(4.24)
где, ![]() - коэффициент радиального зазора
- коэффициент радиального зазора
![]()
![]()
![]()
![]()
Высота зуба
![]() (4.25)
(4.25)
![]()
![]()
![]()
![]()
Толщины зубьев по делительной окружности
![]() (4.26)
(4.26)
![]()
![]()
![]()
![]()
Радиусы основных окружностей
![]() (4.27)
(4.27)
![]()
![]()
![]()
![]()
Углы профиля в точке на окружности вершин
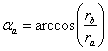 (4.28)
(4.28)
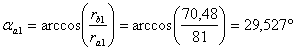
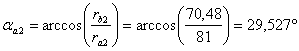
Толщины зубьев по окружности вершин
![]() (4.29)
(4.29)
![]()
![]()
Проверим зубья на заострение
![]() (4.30)
(4.30)
![]() Зубья удовлетворяют условию заострения
Зубья удовлетворяют условию заострения
Угловой шаг зубьев
![]() (4.31)
(4.31)
![]()
![]()
Для 1-го колеса:
![]() (4.32)
(4.32)
где, ![]() - коэффициент относительного скольжения 1-го зубчатого колеса
- коэффициент относительного скольжения 1-го зубчатого колеса
![]() - передаточное отношение от второго колеса к первому
- передаточное отношение от второго колеса к первому
![]() - длина теоретической линии зацепления
- длина теоретической линии зацепления
![]() - переменное расстояние от точки
- переменное расстояние от точки ![]() к точке
к точке ![]()
![]() и
и ![]()
Для 2-го колеса:
![]() (4.33)
(4.33)
Определим масштабный коэффициент относительного скольжения
![]()
Результаты сводим в таблицу
Таблица 4.1 – Коэффициенты скольжения
|
|
|
|
|
|
| 0 |
|
| 1 | 25 |
| 20 | -8,2605 | -206,51 | 0,892014 | 22,3 |
| 40 | -3,13025 | -78,26 | 0,757884 | 18,95 |
| 60 | -1,42017 | -35,50 | 0,586805 | 14,67 |
| 80 | -0,56513 | -14,13 | 0,361073 | 9,03 |
| 100 | -0,0521 | -1,3 | 0,04952 | 1,24 |
| 120 | 0,289917 | 7,25 | -0,40829 | -10,21 |
| 140 | 0,534214 | 13,36 | -1,14691 | -28,67 |
| 160 | 0,717438 | 17,94 | -2,53904 | -63,48 |
| 180 | 0,859944 | 21,5 | -6,14002 | -153,5 |
| 200 | 0,97395 | 24,35 | -37,3877 | -934,69 |
| 224,28 | 1 | 25 |
|
|
Коэффициент перекрытия зубчатой передачи определяем (графически) по формуле
![]() (4.34)
(4.34)
где, ![]() - длина активной линии зацепления
- длина активной линии зацепления
![]() - основной шаг,
- основной шаг, ![]()
![]()
Для определения коэффициента перекрытия зубчатой передачи аналитически воспользуемся формулой
![]() (4.35)
(4.35)
где, ![]() - углы профиля в точке на окружности при вершине
- углы профиля в точке на окружности при вершине
![]() - угол зацепления
- угол зацепления
![]()
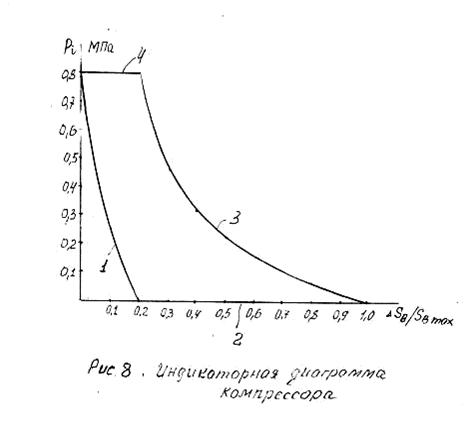
5. Синтез кулачкового механизма 5.1 Вычисление масштабных коэффициентов диаграмм движения толкателя
После построения и графического интегрирования заданного графика аналога ускорения толкателя мы получили диаграмму аналога скорости толкателя, которую также графически интегрируем, в результате также получаем диаграмму аналога пути толкателя.
Исходя из диаграммы пути, определяем масштабные коэффициенты на фазе удаления и фазе возврата. Воспользуемся для этого формулой
![]() (5.1)
(5.1)
где, ![]() - масштабный коэффициент для графика пути,
- масштабный коэффициент для графика пути, ![]()
![]() - ход толкателя,
- ход толкателя, ![]()
![]() - максимальное значение пути,
- максимальное значение пути, ![]()
Для фазы удаления
![]()
![]()
Для фазы возврата
![]()
![]()
Определим масштабный коэффициент по углу![]()
![]() (5.2)
(5.2)
где, ![]() - рабочая фаза,
- рабочая фаза, ![]()
![]() - расстояние между 1-й и 18-й точками на чертеже.
- расстояние между 1-й и 18-й точками на чертеже. ![]()
![]()
![]()
![]()
![]()
Определим масштабные коэффициенты для диаграммы скорости
![]() (5.3)
(5.3)
где, ![]() - масштабный коэффициент скорости,
- масштабный коэффициент скорости, ![]()
![]() - полюсное расстояние на диаграмме скорости,
- полюсное расстояние на диаграмме скорости, ![]()
Для фазы удаления
![]()
![]()
Для фазы возврата
![]()
![]()
Определим масштабные коэффициенты для аналога ускорения
![]() (5.4)
(5.4)
где, ![]() - масштабный коэффициент ускорения,
- масштабный коэффициент ускорения, ![]()
![]() - полюсное расстояние на диаграмме ускорения,
- полюсное расстояние на диаграмме ускорения, ![]()
Для фазы удаления
![]()
![]()
Для фазы возврата
![]()
![]()
Для его нахождения исходными данными являются график пути и график скоростей ![]() и
и ![]() , ход толкателя
, ход толкателя ![]() , угол давления
, угол давления ![]() , эксцентриситет
, эксцентриситет ![]()
На основании этих данных строится зависимость ![]() .
.
По оси ![]() откладываются расстояния пути, которые берутся с графика пути в определённом масштабе, т.к. у нас разные масштабы на фазе удаления и фазе возврата, то мы должны привести их к одному.
откладываются расстояния пути, которые берутся с графика пути в определённом масштабе, т.к. у нас разные масштабы на фазе удаления и фазе возврата, то мы должны привести их к одному.
Найдём поправочные коэффициенты
![]() (5.5)
(5.5)
где, ![]() - поправочный коэффициент
- поправочный коэффициент
![]() - новый масштабный коэффициент, одинаковый для оси
- новый масштабный коэффициент, одинаковый для оси ![]() и
и ![]() , он принимается произвольно.
, он принимается произвольно.
![]()
![]()
Через полученные точки на линии параллельной ![]() откладываем отрезки аналогов скоростей для соответствующего интервала, взятые с графика скорости.
откладываем отрезки аналогов скоростей для соответствующего интервала, взятые с графика скорости.
Отрезок скорости приводится к тому же масштабу, что и графики пути.
Определим поправочные коэффициенты
![]() (5.6)
(5.6)
где, ![]() - поправочный коэффициент
- поправочный коэффициент
![]()
![]()
После построения получили некоторую кривую, к ней под углом ![]() проводим касательные.
проводим касательные.
Из области выбора центра ![]() выбираем с учётом масштаба
выбираем с учётом масштаба
![]()
![]() .
.
Найдём зависимость угла давления ![]() от угла
от угла![]() .
.
![]() (5.7)
(5.7)
где, ![]() - угол давления,
- угол давления, ![]()
![]() - расстояние
- расстояние ![]() ,
, ![]()
![]() - длина коромысла АВ,
- длина коромысла АВ, ![]()
![]() - отрезок скорости,
- отрезок скорости, ![]()
![]() - угол между отрезком АВ и расчётной прямой на чертеже,
- угол между отрезком АВ и расчётной прямой на чертеже, ![]()
Произведём расчёт при ![]()
![]()
![]()
Остальные значения угла давления определяем аналогично, и результаты сносим в таблицу
Таблица 5.1 – Углы давления
|
| 0 | 14,37 | 27,75 | 43,12 | 57,5 | 71,87 | 86,25 | 100,62 | 115 |
|
| -13,56 | 13,91 | 30,29 | 35,8 | 35,27 | 32,23 | 26,84 | 19,45 | 10,04 |
|
| 135 | 152,5 | 170 | 187,5 | 205 | 222,5 | 240 | 257,5 | 275 |
|
| 10,04 | -0,31 | -10,52 | -19,58 | -27,28 | -34,7 | -36,88 | -30,67 | -13,56 |
При построении используем следующие масштабные коэффициенты
![]()
![]()
Определим полярные координаты для построения центрового профиля кулачка.
![]() (5.8)
(5.8)
где, ![]() - радиус вектор,
- радиус вектор, ![]()
![]() - отрезок пути,
- отрезок пути, ![]()
![]() (5.9)
(5.9)
![]()
![]()
![]() (5.10)
(5.10)
Рассчитываем ![]() и
и ![]() для положения 5
для положения 5
![]()
![]()
![]()
![]()
Все остальные значения сводим в таблицу
Таблица 5.2 – Значения полярных координат
| Полож | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||
|
| 0 | 14,37 | 28,75 | 43,12 | 57,5 | 71,87 | 86,25 | 100,62 | 115 | |||||||
|
| 20 | 21,24 | 24,7 | 29,89 | 36 | 42,11 | 47,3 | 50,76 | 52 | |||||||
| Полож | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||||||
|
| 135 | 152,5 | 170 | 187,5 | 205 | 222,5 | 240 | 257,5 | 275 | |||||||
|
| 52 | 50,58 | 46,96 | 41,85 | 36 | 29,53 | 25,04 | 21,42 | 20 | |||||||
Определим масштабный коэффициент для построения кулачка
![]()
![]()
По полученным значениям ![]() и
и ![]() строим центровой профиль кулачка. Для этого в масштабе
строим центровой профиль кулачка. Для этого в масштабе ![]() проводим окружность радиусом
проводим окружность радиусом ![]() .
.
От радиуса ![]() в направлении противоположном вращению кулачка, отложим полярные углы
в направлении противоположном вращению кулачка, отложим полярные углы ![]() , на сторонах которых отложим
, на сторонах которых отложим ![]() . Соединив плавной кривой концы радиусов-векторов получим центровой профиль кулачка.
. Соединив плавной кривой концы радиусов-векторов получим центровой профиль кулачка.
Действительный профиль кулачка найдём, как кривую, отстоящую от центрового профиля на расстоянии, равном радиусу ролика.
Определим радиус ролика
![]() (5.11)
(5.11)
где, ![]() - радиус ролика,
- радиус ролика, ![]()
![]()
![]()
![]() (5.12)
(5.12)
где, ![]() - радиус кривизны профиля кулачка, определяется графически
- радиус кривизны профиля кулачка, определяется графически
Радиус кривизны профиля кулачка приближённо определяется как радиус вписанной окружности участка кулачка, где его кривизна кажется наибольшей. На этом участке произвольно выбираются точки ![]() . Точку
. Точку ![]() соединим с точками
соединим с точками ![]() и
и ![]() . К серединам получившихся хорд восстановим перпендикуляры, точку пересечения которых примем за центр вписанной окружности.
. К серединам получившихся хорд восстановим перпендикуляры, точку пересечения которых примем за центр вписанной окружности.
![]()
![]()
Принимаем ![]()
![]()
На центровом профиле кулачка выбираем ряд точек, через которые проводим окружность с радиусом ролика. Огибающая эти окружности является действительным профилем кулачка.
Литература
1. Артоболевский И.И. Теория механизмов и машин; Учеб. для втузов. – 4-е изд., перераб. и доп. – М.: Наука. 1988;
2. Девойно Г.Н. Курсовое проектирование по теории механизмов и машин. 1986.
Похожие работы
... отрезка "ав". Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скоростей определится из соотношений: . Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении. Как уже говорилось, отрезок плана скоростей ав (вектор) обозначает скорость точки "В" относительно точки ...
... (м); lав=lас== (м); Так как механизм находится в 5 положении, то, деля окружность на 12 частей, т.е. на каждую часть приходится по 30, задаём нужное положение. 2. Киниматическое исследование механизма компрессора 2.1 Построение плана скоростей для заданного 5-го положения. , угловая скорость коленчатого вала , где мин-1 – частота вращения коленчатого вала. ; ; ...
... .335 с., ил. Организационно-экономический расчёт.Консультант: Одинцова Л. А. Исследовательская часть. Охрана труда и охрана окружающей среды. В данном проекте спроектирован цех для ремонта поршневых компрессоров. Основной материал обработки серый чугун марок СЧ 21, 24 ГОСТ 1412-79. Для ремонта компрессоров применяется различное оборудование: токарные, круглошлифовальные, плоскошлифовальные, ...
... "Инструкции по эксплуатации поршневого компрессора". Типичные повреждения и неисправности и указания по их устранению Признаки Причины Способ устранения Другие ненатуральные шумы компрессора а) сильный перегрев, вызывающий заклинивание поршня а) снять и очистить поршень и зеркало цилиндра, проверить качество используемого масла Повышенное давление на выходе или на входе может ...

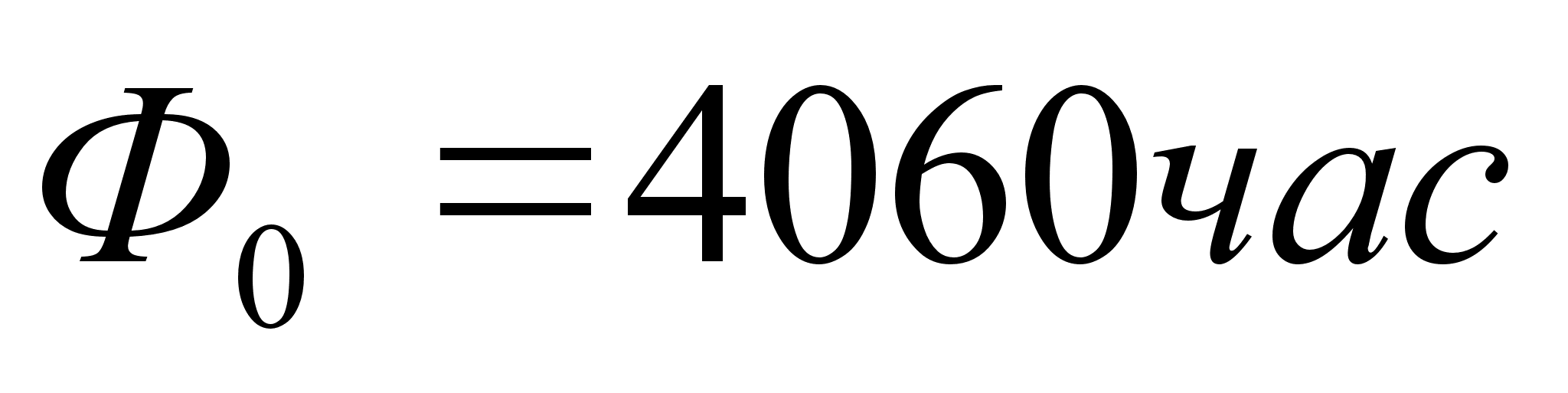
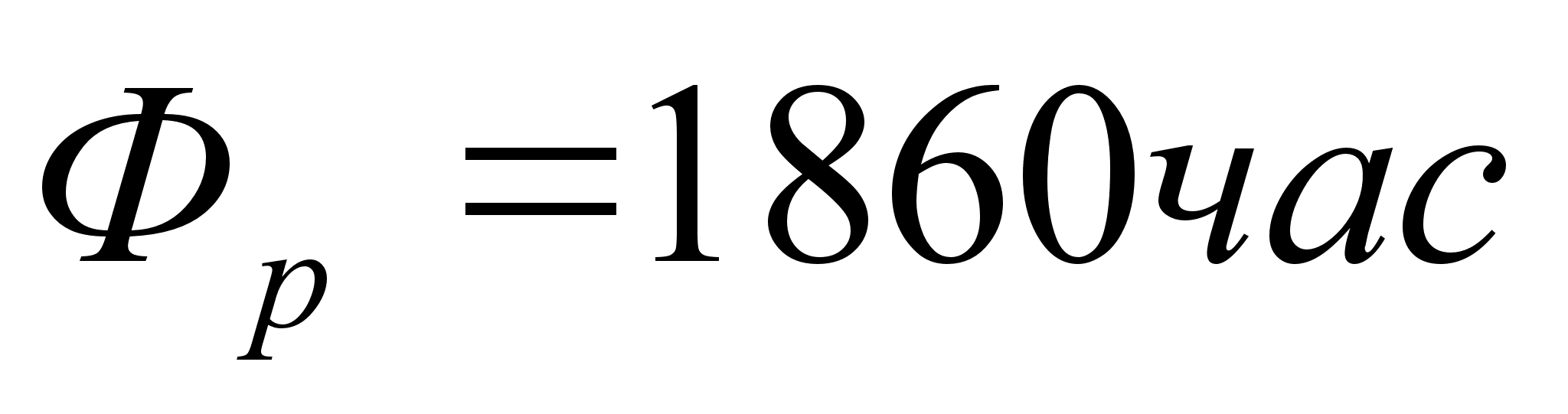


0 комментариев