Реализация модели фильтра в Simulink

3. Реализация модели фильтра в Simulink

Перевели данные содержащие электрокардиограмму (приложение 1) из MSExcel в MATLAB и построили график кардиосигнала (рисунок 7).

>> plot(G)

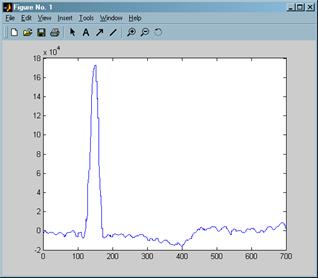
Рисунок 7

Затем наложили на исходный сигнал помеху (рисунок 8):

n=length(G);

e=rand(n)*17225

for i=1:n

s(i)=e(i)+G(i)

end

>> plot(s)

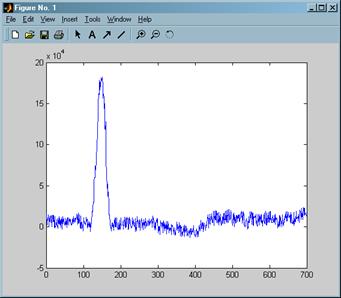
Рисунок 8

r=0

for i=1:n;

r=r+1;

t(i)=r;

end

t1=t'

S=s’

В приложении Simulink собрали схему, реализующую модель данного фильтра (рисунок 9).

Рисунок 9

На вход фильтра подается сигнал с помехой. Значения коэффициентов полиномов передаточной функции взяты из рабочей области MATLAB. На рисунке 10 представленны результаты фильтрации и исходный сигнал с помехой.

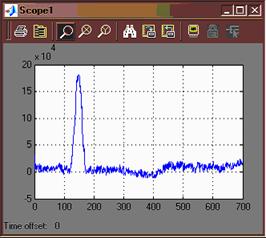
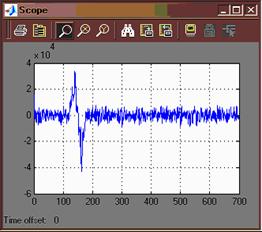
Рисунок 10

Заметим, что результат фильтрации неудовлетворителен, появляется значительный по амплитуде отрицательный выброс, в то время как амплитуда R-зубца уменьшается почти в четыре раза.

4. Реализация полосового фильтра в цифровой форме

Итак для фильтрации электрокардиосигнала аналоговый полосовой фильтр оказался молоэффективен. Однако, MATLAB предоставляет широкие возможности для проектирования различных фильтров (в том числе и полосно-пропускающего) в цифровой форме.

В MATLAB существует библиотека (toolbox) Filter Design, предназначенная для решения задач проектирования, включая процедуры коррекции полученных результатов с учётом эффектов квантования. Библиотека имеет интерактивную графическую программу (GUI) fdatool, с помощью которой можно рассчитывать цифровые фильтры.

Сразу после загрузки программы отображается главное окно библиотеки. В нем мы задали параметры проектируемого фильтра (рисунок 11) в соотфетствии с полученными ранее ЛАЧХ И ФЧХ.

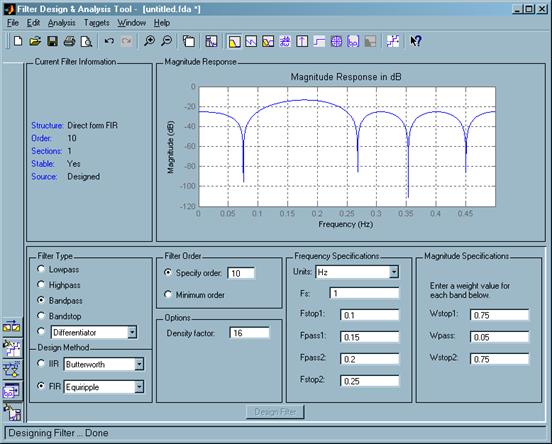
Рисунок 11

Воспользовавшись кнопками Import filter, Filter Coefficient, вывели значения коэффициентов фильтра (рисунок 12).

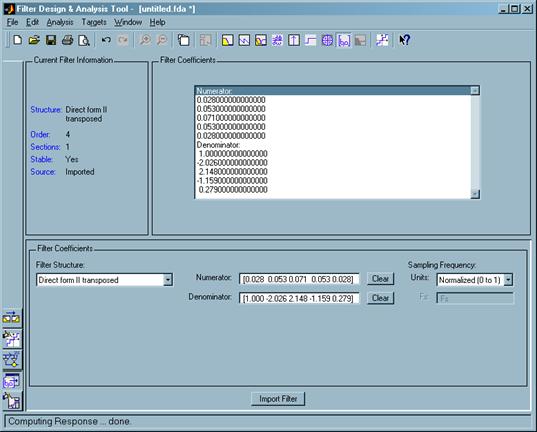
Рисунок 12

Последовательно выбирая команды Magnitude Recponse, Phase Recponse, Impulse Recponse, Step Recponse, определили характеристики фильтра.

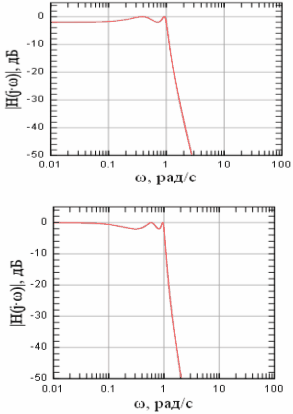
Амплитудно-частотная характеристика фильтра (рисунок 13)

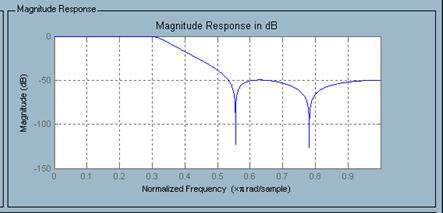
Рисунок 13

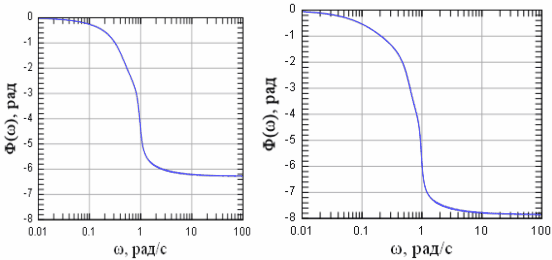
Фазо-частотная характеристика (рисунок 14)

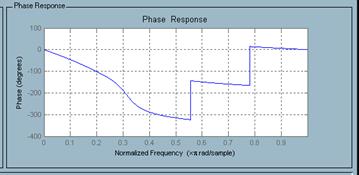
Рисунок 14

Импульсная характеристика (рисунок 15)

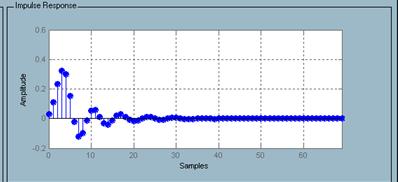
Рисунок 15

Отклик на единичное воздействие (рисунок 16)

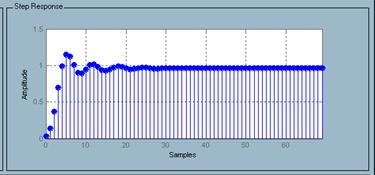
Рисунок 16

5. Реализация модели фильтра в Simulink

Нажав на кнопку  мы получаем созданный фильтр в виде блока-элемента библиотеки Simulink. Дважды щелкнув мышью на изображении этого блока можно получить его внутреннюю структуру (рисунок 17)

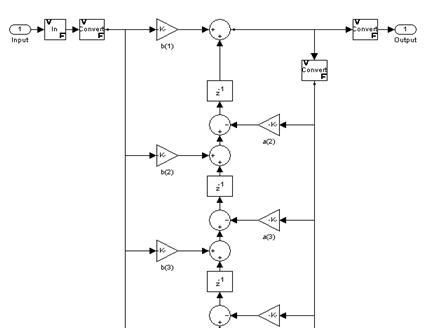
Рисунок 17

На рисунке 18 представлена схема, реализующая модельданного фильтра.

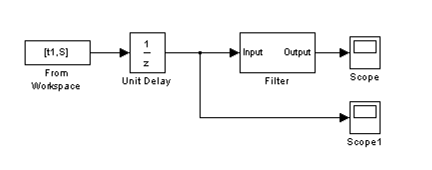
Рисунок 19

На вход фильтра подавали тот же сигнал, что и при исследовании аналогового фильтра

На рисунке 20 представлены результаты фильтрации и исходный сигнал с помехой.

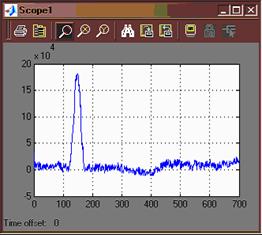
Рисунок 20

При сравнении двух осциллограмм можно говорить об удовлетворительном результате фильтрации.

6. Исследование характеристик WAVELET и WAVELET-преобразований одномерных сигналов

 

Тoolbox Wavelet – набор инструментов, встроенных в вычислительную среду MATLAB, для решения разнообразных инженерных задач, связанных с компрессией сигналов, анализом их особенностей, очисткой от шумов и др. В основе используемых процедур лежит относительно новая теория разложения сигналов по специальным функциям всплескам (wavelet), главные особенности которых ограниченность во времени, самоподобие и компактная локализация энергии по времени и частоте.

Тулбокс Wavelet состоит из набора подпрограмм, которые позволяют:

·           ознакомиться и исследовать характеристики индивидуальных wavelet и wavelet-пакетов;

·           вычислять непрерывное wavelet-преобразование одномерных сигналов;

·           производить анализ и синтез дискретных одномерных и двумерных сигналов на основе дискретного wavelet-преобразования;

·           раскладывать одно- и двумерные сигналы по пакету wavelet;

·           исследовать статистические характеристики сигналов;

·           производить сжатие и очистку от шума одномерных и двумерных сигналов.

Wavemenu запускается из командной строки MATLAB командой «wavemenu».

В качестве исходного сигнала используем все тот же сигнал ЭКГ с наложенной на него помехой (рисунок 21):

Рисунок 21

Wavelet-преобразование позволяет разложить сигнал по компактным, хорошо локализованным по времени и частоте, базисным функциям, что позволяет, в отличие от преобразования Фурье, описывать нестационарные сигналы. При этом важно, что такое разложение достаточно экономно в вычислительном отношении.

В отличие от кратковременного преобразования Фурье (STFT), непрерывное wavelet-преобразование (CWT) имеет переменное разрешение по времени и частоте. В области высоких частот оно обеспечивает хорошее разрешение по времени и плохое по частоте, а в области низких частот хорошее разрешение по частоте и плохое по времени (рис. 3). Применение wavelet-преобразования дает хорошие результаты, особенно когда компоненты сигнала с высокой частотой имеют небольшую длительность, а низкочастотные компоненты достаточно большую. Практически все биологические сигналы имеют подобную структуру.

Выбрали wavelet Добеши с двумя уровнями декомпозиции (ортогональный фильтр с конечной маской) (рисунок 22).

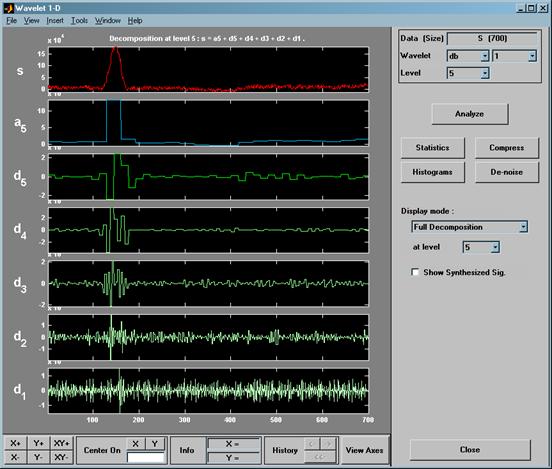
Рисунок 22

Дискретное wavelet-преобразование наиболее эффективно в задачах сжатия сигналов и изображений, задаче очистки сигнала от шумов.

Нажатие на кнопку Stanistics позволяет получить статистические данные относительно исследуемого сигнала (рисунок 23).

При сжатии сигнала используют следующую схему: производится wavelet-преобразование исходного сигнала, после чего запоминаются только значащие коэффициенты, то есть те, которые больше некоторого заданного порога. Восстановление сигнала производится при помощи обратного wavelet-преобразования, при этом пропущенные коэффициенты заменяются нулями.

Результаты сжатия представлены на рисунке 24.

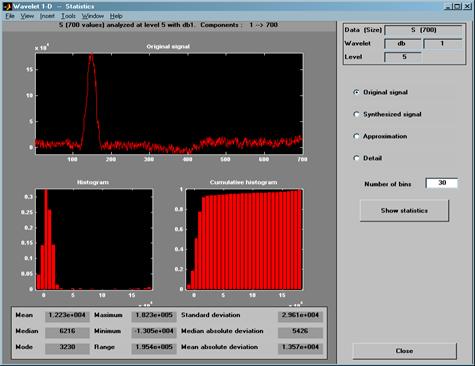
Рисунок 23

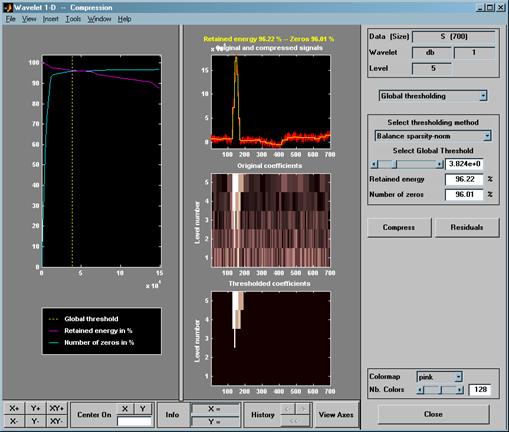
Рисунок 24

Графический интерфейс позволяет решать задачи уменьшения уровня шума в дискретном (цифровом) сигнале (очистки от шума). Для этого необходимо нажать на кнопку «Denoise» в середине правой колонки, под кнопкой «Analyze». Параметры и результаты уменьшения шума представлены на рисунке 25.

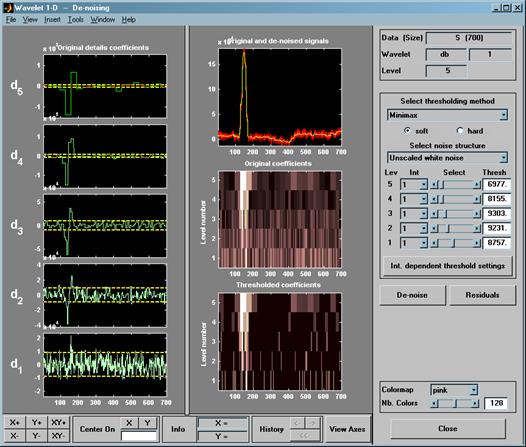
Рисунок 25

На рисунке 26 подробнее представлен результат очистки сигнала от шума.

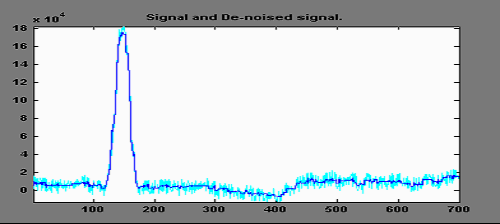
Рисунок 26

Заключение

В ходе курсового проекта быди получены навыки современных методов обработки биомедицинских сигналов с использованием средств вычислительной техники. Выполняя курсовой проект исследовали аналоговый и цифровой полосно-пропускающий фильтр, реализовали модель фильтра в Simulink, а также познакомились с wavelet-преобразованиями.

Методы цифровой обработки сигналов приобрели большую важность ввиду того, что теперь они не только заменяют классические аналоговые методы во многих традиционных областях техники, но и применяются во многих новых областях, таких как медицинская техника.

Дискретное wavelet-преобразование наиболее эффективно в задачах сжатия сигналов и изображений, задаче очистки сигнала от шумов.

Список использованных источников

1.  Джонсон Д. Справочник по активным фильтрам. – М.: Энергоатомиздат, 1983

2.  Макс Жак Методы и техника обработки сигналов при физических измерениях. Пер. с фр. Под ред Волкова Н.Г. – М.: Мир, 1983

3.  Дьяконов В. Simulink 4. Специальный справочник. – СПб.: Питер, 2002

4.  Андреев И.И., Ланнэ А.А. MATLAB для DSP: SPTool – инструмент для расчёта цифровых фильтров и спектрального анализа сигналов // Цифровая обработка сигналов. 2000. №2.

5.  Потемкин В.Г. MATLAB 5 для студентов /Диалог-МИФИ. 1999.