Навигация
Оценка рациональной формы поперечного сечения с точки зрения прочности
3. Оценка рациональной формы поперечного сечения с точки зрения прочности
Наиболее рациональным по расходу материала является швеллер или двутавр, так как для обеспечения прочности при одинаковых условиях площадь поперечного сечения у них наименьшая. Выбираем двутавр.
4. Проверка выбранного поперечного сечения на прочность касательного напряжения
Условие прочности по касательным напряжениям имеет вид:
τmax = ![]() ≤ [τ]
≤ [τ]
[τ] = 390 МПа – допускаемое касательное напряжение.
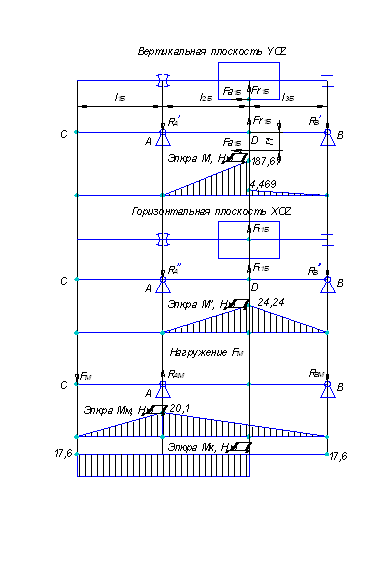
Из эпюры поперечных сил:
Qmax = 29,4 т = 29,4 · 104 Н – максимальная поперечная сила.
Из справочника (двутавр №36):
Sx = 423 см3 = 423 · 10-6 м3 – статический момент полусечения расположенного выше или ниже нейтральной оси.
Ix = 13380 cм4 = 13380 · 10-8 м4 – момент инерции всего сечения относительно нейтральной линии.
b = d = 7,5 мм = 0,0075 м – толщина стенки двутавра.
τmax = ![]() = 124 · 106 Па = 124 МПа
= 124 · 106 Па = 124 МПа
τmax = 124 МПа ≤ [τ] = 390 МПа
5. Построение эпюр нормальных и касательных напряжений в опасном сечении балки
Определим наибольшие нормальные напряжения в сечении балки с максимальным изгибающим моментом.
σmax = ± Mmax / Wx = ±(48,22 · 104) / 0,000743 = ± 648 МПа,
min
так как для двутавра №36 Wx = 743 см3 = 0,000743 м3.
Из теории известно, что наибольшие нормальные напряжения при поперечном изгибе возникают в крайних волокнах сечения, в нейтральном слое напряжение равно нулю. Строим эпюру нормальных напряжений. Для этого в произвольном масштабе изображаем сечение двутавра. Параллельно вертикальной оси двутавра проводим нулевую линию и откладываем от нее по разные стороны на уровне крайних волокон σmax и σmin. Соединяем эти точки прямой линией.
Наибольшие касательные напряжения найдены выше. τmax = 124 МПа
Наибольшие касательные напряжения по высоте сечения возникают на уровне нейтральной оси.
Строим эпюру касательных напряжений (рис. 2).
На нулевой линии на уровне нейтральной оси откладываем τmax. Зная характер эпюры, даем ее полное изображение.
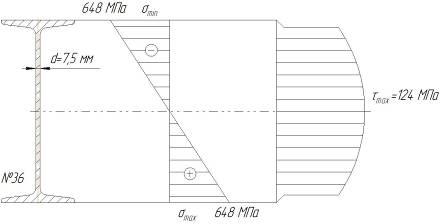
Рис. 2.
6. Проверка на прочность балки по эквивалентным напряжениям
Рассмотрим элемент, вырезанный в районе точки А (рис. 3). На гранях этого элемента, совпадающих с поперечными сечениями, возникают максимальные нормальные напряжения. В точке А возникает линейное напряженное состояние, поэтому условие прочности имеет вид:
σmax ≤ [σ]
Очевидно, что:
σmax = σА = Mmax / Wx = (48,22 · 104) / 0,000743 = 648 МПа
σmax = 648 МПа ≤ [σ] = 650 МПа.
Рассмотрим элемент, вырезанный в районе точки В (рис. 3). На его гранях, совпадающих с поперечными сечениями, возникают максимальные касательные напряжения (точка В находится в нейтральном слое).
τmax = τВ = ![]() =
= ![]() = 124 · 106 Па = 124 МПа
= 124 · 106 Па = 124 МПа
В точках нейтрального слоя возникает плоское напряженное состояние – чистый сдвиг. Как известно, при чистом сдвиге:
σ1 = |σ3| = τ; то есть:σ1 = |σ3| = τmax = τВ = 124 МПа
По гипотезе прочности наибольших касательных напряжений:
σэкв = σ1 – (-σ3) = σ1 + σ3 = 2τВ = 2 · 124 = 248 МПа
σэкв = 248 МПа ≤ [σ] = 650 МПа.
Вероятно опасной точкой может быть точка С (точка на границе полки и стенки двутавра). В этой точке возникают нормальные напряжения, близкие по значению к максимальным и значительные касательные напряжения (рис. 3).
σС = ![]() =
= ![]() = 604 · 106 Па = 604 МПа
= 604 · 106 Па = 604 МПа
τС = ![]() =
= ![]() = 91 · 106 Па = 91 МПа
= 91 · 106 Па = 91 МПа
Sx’ – статический момент площади полки относительно оси х. Принимая полку за прямоугольник с размерами: 145х12,3, находим:
Sx’ = 145 · 12,3 · 173,85 = 3,1 · 105 мм3 = 3,1 · 10-4 м3
В точке С возникает плоское напряженное состояние. По гипотезе наибольших касательных напряжений находим:
σэкв = ![]() =
= ![]() = 631 МПа
= 631 МПа
σэкв = 631 МПа ≤ [σ] = 650 МПа.
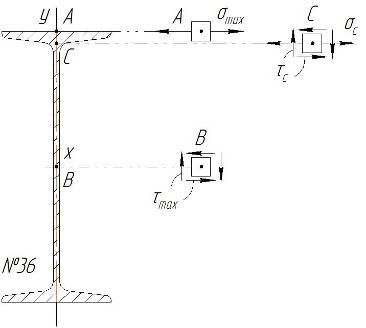
Рис. 3.
Похожие работы
... и строим эпюры (рис.4,в и рис.5,в) 1 вариант: φ0 = φА = 0 мрад мрад мрад 2 вариант: φ0 = φВ = 0 мрад мрад мрад 3 Процедура создания стержней 3.1 Создание стальной балки Спроектировать стальную балку (рис. 6,а) в 5 вариантах поперечного сечения: круглого, прямоугольного (h/b=2), двутаврового, из швеллеров и уголков, приняв допускаемое напряжение ...
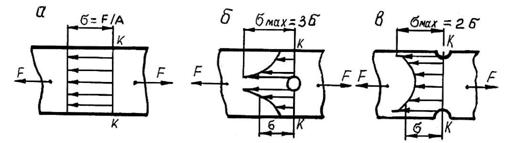
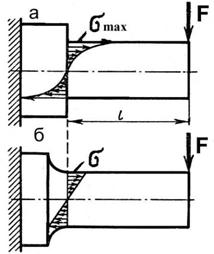
... Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как или и далее величину диаметра вала . Местные напряжения Напряжения при растяжении (сжатии), изгибе, кручении и сложных деформациях, определяемые по рассмотренным выше зависимостям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, в местах ...
... представление о характере изменения силового фактора по длине или координате и позволяют установить местонахождение опасных сечений. 20. Сформулировать основные гипотезы и допущения, принятые в сопротивлении материалов. 1) Гипотеза о сплошном строении тела. 2) Гипотеза об идеальной упругости материала. 3) Гипотеза об однородности материала. 4) Гипотеза об изотропности материала. ...
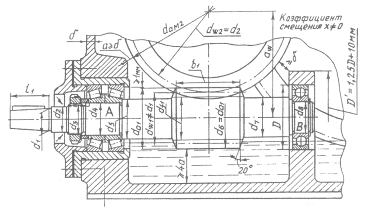
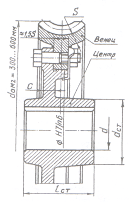
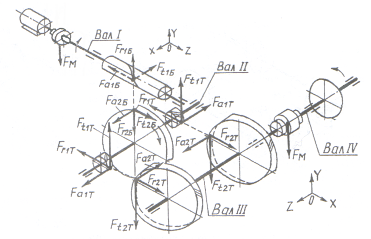
... валиками (индекс М), шаг : д)конструктивные особенности: на валу установлена одна звёздочка для тяговой пластинчатой цепи; приводной вал конвейера соединён с выходным валом редуктора посредством горизонтально расположенной цепной передачи; е) расчётный срок службы; ж) кратковременная перегрузка ; з) номер типового режима нагружения - 2. 10.1 Предварительная разработка конструкции ...
0 комментариев