Навигация
Длину магнитной линий снимаем с учетом масштаба с эскиза магнитной цепи. La = 0,1625 м.
Падение магнитных потенциалов в сердечнике якоря
![]() , (4.24)
, (4.24)
![]()
Результаты вышеприведенных и последующих расчетов сведены в таблицу 4.1.
4.5 Участок зубцового слоя якоряПлощадь в расчетном сечении зубцового якоря
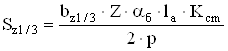 , (4.25)
, (4.25)
![]()
Индукция в расчетном сечении зубцового якоря
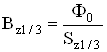 , (4.26)
, (4.26)
![]()
По индукции ![]() = 1,8 Тл, согласно [1], находим напряженность магнитного поля,
= 1,8 Тл, согласно [1], находим напряженность магнитного поля,![]() 14200 А/м.
14200 А/м.
Магнитное напряжение зубцов якоря
![]() , (4.27)
, (4.27)
![]()
4.6 Участок сердечника главного полюса
Площадь сечения сердечника главного полюса
![]() , (4.28)
, (4.28)
![]()
Индукция в сердечнике главного полюса
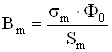 , (4.29)
, (4.29)
![]()
По индукции ![]() =1,7 Тл, согласно [1],находим напряженность Нm = 7050 А/м.
=1,7 Тл, согласно [1],находим напряженность Нm = 7050 А/м.
Падение магнитных потенциалов в сердечнике главных полюсов
![]() , (4.30)
, (4.30)
где Lm – длина силовой линии из эскиза. Lm = 0,12 м.
![]() Fm = 7050 · 0,12 = 846 А.
Fm = 7050 · 0,12 = 846 А.
Магнитное напряжение этого участка Fmj, оценивают по приближенной эмпирической формуле
![]() , (4.31)
, (4.31)
![]()
Площадь сечения участка поворота магнитного потока Sj’, зависит от толщины остова в месте расположения главных полюсов
![]() , (4.32)
, (4.32)
![]()
Индукция на участке выхода потока из полюса в остов
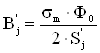 , (4.33)
, (4.33)
![]()
Магнитное напряжение на участке выхода потока из полюса в остов
![]() , (4.34)
, (4.34)
где Hj’– магнитная напряженность на участке перехода из полюса в остов,
согласно[1], Hj’ = 6800 А/м;
Lj’– длина силовой линии на участке поворота потока в остове.
Lj’ = 0,08 м.
DFj’ = 6800 ∙ 0,08 = 544 А.
4.9 Ярмо остова
Площадь сечения ярма остова
![]() , (4.35)
, (4.35)
Sj = 0,06053 · 0,7234 = 0,043787 м2.
Индукция в остове
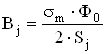 , (4.36)
, (4.36)
![]()
Магнитное напряжение в ярме остова
![]() , (4.37)
, (4.37)
где Hj – магнитная напряженность в остове, согласно [1], Hj = 2010 А/м;
Lj – длина силовой линии в ярме остова, из эскиза магнитной цепи.
Lj’ = 0,644 м.
DFj = 2010∙ 0,644 = 1294,44 А.
4.10 Расчет воздушного зазора
Таблица 4.1 – Расчет магнитных напряжений и МДС возбуждения
| Номер участка | Наименование участка | Магнитный поток, Вб | Сечение, м2 | Индукция, Тл | Напряженность, А/м | Длина силовой линии, м | Магнитное напряжение, А |
| 1 | Сердечник якоря | 0,058 | 0,032439 | 1,8 | 14200 | 0,1625 | 2307,5 |
| 2 | Зубцовый слоя якоря | 0,117 | 0,064876 | 1,8 | 14200 | 0,0331 | 470,02 |
| 3 | Зубцовый слой полюса | – | – | – | – | – | – |
| 4 | Сердечник полюса | 0,123 | 0,072127 | 1,7 | 7050 | 0,12 | 846 |
| 5 | Стык полюса с остовом | – | – | – | – | – | 136 |
| 6 | Переход из полюса в остов | 0,061 | 0,036862 | 1,66 | 6800 | 0,08 | 544 |
| 7 | Ярмо остова | 0,061 | 0,043787 | 1,4 | 2010 | 0,644 | 1294,44 |
| Сумма магнитных напряжений стальных участков | 5597,96 | ||||||
| 8 | Воздушный зазор | 0,117 | 0,001947 | 0,86 | – | – | 4248,19 |
| МДС намагничивания | 9846,15 | ||||||
| МДС на компенсацию действия реакции якоря | 918,3 | ||||||
| МДС Возбуждения обмотки главного полюса | 10764,45 | ||||||
Потребная МДС воздушного зазора для обеспечения заданных свойств двигателя
![]() , (4.38)
, (4.38)
где ![]() – коэффициент использования мощности.
– коэффициент использования мощности.
При ![]() ,
,![]() . Принимаю
. Принимаю ![]() = 0,8;
= 0,8;
![]() – коэффициент регулируемости по скорости;
– коэффициент регулируемости по скорости;
![]() – коэффициент магнитной устойчивости;
– коэффициент магнитной устойчивости;
![]() – МДС поперечной реакции якоря.
– МДС поперечной реакции якоря.
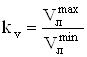 , (4.39)
, (4.39)
![]() .
.
![]() , (4.40)
, (4.40)
![]()
В машинах без компенсационной обмотки, для снижения воздействия поперечной реакции якоря наконечникам главных полюсов придают особую форму, так чтобы зазор расходился бы к краям полюса. Расходящиеся воздушные зазоры обеспечивают нарастание магнитного сопротивления потоку поперечной реакции якоря соответственно росту её МДС от центра главного полюса. Очевидно, что степень искажения магнитного поля главных полюсов, а значит, и величина максимальных межламельных напряжений в этом случае зависят от формы и величины воздушного зазора. Поэтому коэффициент магнитной устойчивости в некомпенсированных двигателях определяется специальным расчетом с учетом индивидуальных особенностей проектируемой машины.
Коэффициент максимального искажения магнитного поля
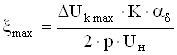 , (4.41)
, (4.41)
где ![]() – максимальный уровень межламельного напряжения.
– максимальный уровень межламельного напряжения.
Принимаю ![]()
![]()
Коэффициент раскрытия воздушного зазора принимаю, ![]()
Тогда согласно [1], рисунок 8.3 ![]()
![]()
Согласно закону полного тока, сумма падений магнитных напряжений в контуре должна компенсироваться МДС намагничивания
![]() , (4.42)
, (4.42)
![]()
Реальное значение МДС возбуждения главных полюсов
![]() , (4.43)
, (4.43)
где ![]() – поперечная составляющая реакции якоря.
– поперечная составляющая реакции якоря.
Наиболее простым методом нахождения составляющей ![]() является ее расчет через коэффициент реакции якоря
является ее расчет через коэффициент реакции якоря
![]() , (4.44)
, (4.44)
В двигателях без компенсационной коэффициент реакции якоря, ![]() определяется по диаграмме рисунка 8.4.
определяется по диаграмме рисунка 8.4.
Для индукции ![]() Тл, принимаем
Тл, принимаем ![]() .
.
![]()
![]()
При этом удостоверяемся в правильности выбора ![]() по формуле
по формуле
![]()
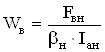 , (4.45)
, (4.45)
![]()
Так как число витков округлили, то необходимо уточнить потребную МДС воздушного зазора. Для этого уточним реальное значение МДС возбуждения главных полюсов.
![]() , (4.46)
, (4.46)
![]()
![]() , (4.47)
, (4.47)
![]()
![]() , (4.48)
, (4.48)
![]()
Для определения точных геометрических размеров воздушного зазора сначала рассчитаем эквивалентный воздушный зазор
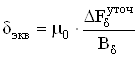 , (4.49)
, (4.49)
где ![]() – магнитная постоянная.
– магнитная постоянная. ![]() Гн/м.
Гн/м.
![]() м.
м.
Связь между конструкционными и эквивалентными воздушными зазорами устанавливается через коэффициент Картера по поверхности якоря, учитывающий геометрические размеры зубцового слоя якоря
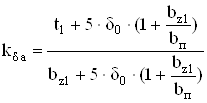 . (4.50)
. (4.50)
Принимаю ![]() = 3,183 мм.
= 3,183 мм.
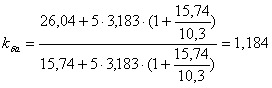 .
.
Найдем коэффициент Картера по поверхности полюса для эксцентричного зазора
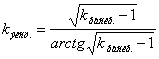 , (4.51)
, (4.51)
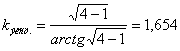 .
.
![]() , (4.52)
, (4.52)
![]()
При нахождении параметров катушки главных полюсов, одним из решающих значений для вписывания катушки, является сечение проводника обмотки возбуждения. Принимаю класс изоляции «В» и плотность тока равную
jв = 3,5 А/мм2. (4.53)
Далее рассчитываю пределы, в которых должно находиться сечение проводника обмотки возбуждения.
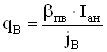 , (4.54)
, (4.54)
![]() мм2.
мм2.
Катушки главных полюсов при 2р = 2 выполняются намоткой проводников на широкое ребро. Выбираю размеры проводника, согласно[1]
hпр × bпр = 25 × 1,81 qв = 44,6 мм2. (4.55)
Примем: Dмв = 0,5 мм, Dразд = 1 мм, Dвыст = 0,5 мм.
Найдем размер катушки по высоте hвк
![]() , (4.56)
, (4.56)
![]()
Разбиваем общее число витков на два слоя
![]() (4.57)
(4.57)
Тогда размеры катушки по ширине ![]() при намотке на широкое ребро
при намотке на широкое ребро
![]() , (4.58)
, (4.58)
![]() , (4.59)
, (4.59)
![]()
![]()
Исходя из полученных размеров катушки, рассчитывается средняя длина одного витка обмотки возбуждения для верхнего и нижнего слоя
![]() , (4.60)
, (4.60)
![]() , (4.61)
, (4.61)
![]()
![]()
Общая длина меди обмоток возбуждения Lв
![]() , (4.62)
, (4.62)
![]()
Сопротивление обмотки возбуждения при 20°С
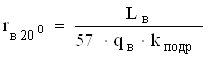 , (4.63)
, (4.63)
где kподр – коэффициент, учитывающий подрез катушки. kподр = 1.
![]()
Масса меди катушек главных полюсов mмв
![]() , (4.64)
, (4.64)
![]()
5 Расчет стационарной коммутации
Целью данного расчета является нахождение среднего за период коммутации значения реакции ЭДС. Расчет выполняется на основе ранее полученных параметров активного слоя, коллектора и щеток. Необходимо обеспечить выполнение ограничения по допустимой величине средней реактивной ЭДС.
Рассмотрим четыре характерных области замыкания потоков пазового рассеяния
![]() , (5.1)
, (5.1)
где ![]() – суммарный удельный коэффициент индуктивности;
– суммарный удельный коэффициент индуктивности;
![]() – магнитная проводимость в пазу якоря над медью;
– магнитная проводимость в пазу якоря над медью;
![]() – то же для части паза, занятой медью проводников;
– то же для части паза, занятой медью проводников;
![]() – то же по коронкам зубцов якоря;
– то же по коронкам зубцов якоря;
![]() – то же для лобовых частей обмотки якоря.
– то же для лобовых частей обмотки якоря.
Удельная магнитная проводимость части паза, занятой медью
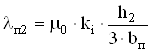 , (5.2)
, (5.2)
где ![]() – высота части паза, занятой медью проводников;
– высота части паза, занятой медью проводников;
![]() – коэффициент экранирующего эффекта от вихревых токов.
– коэффициент экранирующего эффекта от вихревых токов.
Определяю ![]() из полной высоты паза
из полной высоты паза
![]() , (5.3)
, (5.3)
где ![]() – односторонняя толщина изоляции якорной катушки;
– односторонняя толщина изоляции якорной катушки;
![]() – высота клина;
– высота клина;
![]() – общее число прокладок на дне паза и под клином;
– общее число прокладок на дне паза и под клином;
![]() – толщина прокладок.
– толщина прокладок.
Одностороннюю толщину изоляции вычисляем по формуле
![]() , (5.4)
, (5.4)
![]()
![]()
Рассчитаем приведенную высоту элементарного проводника паза якоря
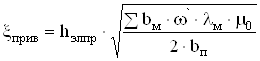 , (5.5)
, (5.5)
где ![]() – высота элементарного проводника в пазу якоря;
– высота элементарного проводника в пазу якоря;
![]() – суммарная ширина меди в пазу;
– суммарная ширина меди в пазу;
![]() – угловая частота коммутации одного паза;
– угловая частота коммутации одного паза;
![]() – удельная проводимость меди при ожидаемой рабочей
– удельная проводимость меди при ожидаемой рабочей
температуре. ![]() = 35 · 106 см/м.
= 35 · 106 см/м.
Для этого найдем величину ![]()
![]()
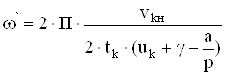 , (5.6)
, (5.6)
где ![]() – окружная скорость на поверхности коллектора в
– окружная скорость на поверхности коллектора в
номинальном режиме;
![]() – коэффициент щеточного перекрытия.
– коэффициент щеточного перекрытия.
![]() , (5.7)
, (5.7)
![]()
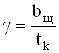 , (5.8)
, (5.8)
![]() .
.
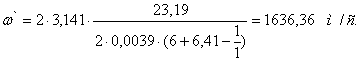
 .
.
По диаграмме рисунка 9.2, согласно [1], найдем величину коэффициента демпфирования. ![]() = 1.
= 1.
![]()
Удельная магнитная проводимость части паза над медью
![]() , (5.9)
, (5.9)
где ![]() – коэффициент, учитывающий материал бандажа крепления
– коэффициент, учитывающий материал бандажа крепления
якорной обмотки. При клиновом креплении из стеклопластов
принимается ![]() =1.
=1.
Найдем величину h1
![]() , (5.10)
, (5.10)
![]()
![]() Гн/м.
Гн/м.
Удельная магнитная проводимость по коронкам зубцов
 , (5.11)
, (5.11)
где ![]() – коэффициент Картера для поверхности якоря под добавочным полюсом.
– коэффициент Картера для поверхности якоря под добавочным полюсом.
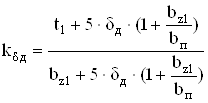 , (5.12)
, (5.12)
Зададимся величиной воздушного зазора между якорем и добавочным полюсом
![]() , (5.13)
, (5.13)
![]()
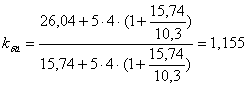 .
.
Рассчитаем ширину наконечника добавочного полюса
![]() , (5.14)
, (5.14)
![]() мм.
мм.
![]() Гн/м.
Гн/м.
С учетом распушения магнитный поток добавочного полюса должен перекрывать пространство, называемое зоной коммутации
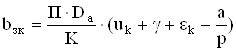 , (5.15)
, (5.15)
![]()
Удельная магнитная проводимость по лобовым частям при немагнитных бандажах крепления лобовых вылетов
 , (5.16)
, (5.16)
![]()
![]()
Найдем среднее за период коммутации значение реактивной ЭДС
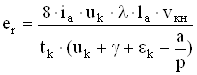 , (5.17)
, (5.17)
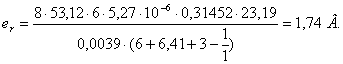
С ростом средней реактивной ЭДС увеличиваются абсолютные небалансы между ступенчатой кривой реактивной ЭДС и плавной кривой распределения коммутирующей ЭДС от потока добавочных полюсов.
Поэтому устанавливается ограничение на значение средней реактивной ЭДС в номинальном режиме
![]() . (5.18)
. (5.18)
1,74 ![]() (3,5…4,0)В.
(3,5…4,0)В.
6 Расчет добавочных полюсов
Из условия равенства реактивной и коммутирующей ЭДС рассчитаем требуемую индукцию в зоне коммутации
 , (6.1)
, (6.1)
где ![]() – окружная скорость на поверхности якоря в номинальном режиме.
– окружная скорость на поверхности якоря в номинальном режиме.
![]() . (6.2)
. (6.2)
![]() м/с.
м/с.
![]() Тл.
Тл.
Для обеспечения требуемого уровня магнитной индукции в зоне коммутации необходимо создать коммутирующий поток
![]() , (6.3)
, (6.3)
![]() Вб.
Вб.
Полный поток добавочных полюсов
![]() , (6.4)
, (6.4)
где ![]() – коэффициент рассеяния добавочного полюса;
– коэффициент рассеяния добавочного полюса;
![]() = 3 – в машинах без компенсационной обмотки.
= 3 – в машинах без компенсационной обмотки.
![]() Вб.
Вб.
Чтобы обеспечить линейность магнитной характеристики добавочных полюсов во всем рабочем диапазоне тока якоря, включая и режим максимальной мощности, индукция в сердечнике полюса в номинальном режиме не должна превышать
![]() Тл. (6.5)
Тл. (6.5)
Принимаю ![]() .
.
Наметим ширину сердечника добавочного полюса
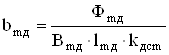 , (6.6)
, (6.6)
где ![]() – длина сердечника полюса.
– длина сердечника полюса. ![]() м;
м;
![]() – коэффициент заполнения сердечника сталью.
– коэффициент заполнения сердечника сталью.
![]() = 1.
= 1.
![]() мм.
мм.
Зададимся значением второго воздушного зазора
![]() мм, (6.7)
мм, (6.7)
![]() мм.
мм.
Магнитное напряжение первого воздушного зазора
 , (6.8)
, (6.8)
![]() А.
А.
Магнитное напряжение второго воздушного зазора
 , (6.9)
, (6.9)
Найдем значение индукции в сердечнике добавочного полюса
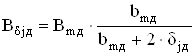 , (6.10)
, (6.10)
![]() Тл.
Тл.
![]() А.
А.
Полная МДС обмотки возбуждения добавочных полюсов
![]() , (6.11)
, (6.11)
![]() А.
А.
Число витков катушки добавочного полюса
 , (6.12)
, (6.12)
![]() витка.
витка.
Так как число витков округляли, то необходимо уточнить значение МДС обмотки возбуждения добавочных полюсов
![]() , (6.13)
, (6.13)
![]() А.
А.
![]() , (6.14)
, (6.14)
![]() А.
А.
![]() , (6.15)
, (6.15)
![]() А.
А.
Скорректируем размеры второго воздушного зазора
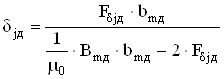 , (6.16)
, (6.16)
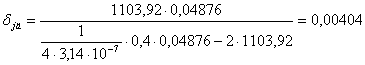 м.
м.
Оценим площадь поперечного сечения проводников обмотки
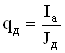 , (6.17)
, (6.17)
где J![]() - максимально допустимая плотность тока в проводниках обмотки, принимаю J
- максимально допустимая плотность тока в проводниках обмотки, принимаю J![]() = 3,5 А/мм
= 3,5 А/мм![]()
![]() мм2.
мм2.
Укладку производим на широкое ребро в семь слоев по высоте тела добавочного полюса.
По значению q![]() намечаем размеры проводника обмотки возбуждения добавочных полюсов
намечаем размеры проводника обмотки возбуждения добавочных полюсов
hпр × bпр = 22 × 1,81, qд = 39,1 мм2, (6.18)
Найдем размер катушки по высоте в нашем случае
![]() , (6.19)
, (6.19)
![]() мм.
мм.
Тогда размеры четырех крайних к остову слоев катушки по ширине, при условии, что в них по 12 витков
![]() , (6.20)
, (6.20)
![]() мм.
мм.
Средняя длина витка добавочного полюса
![]() , (6.21)
, (6.21)
![]() м.
м.
Сопротивление цепей обмоток добавочных полюсов 20°С
![]() , (6.22)
, (6.22)
![]() Ом.
Ом.
Масса меди катушек добавочных полюсов
![]() , (6.23)
, (6.23)
![]() кг.
кг.
Список использованных источников
1 Андросов Н. Н., Дурандин М.Г. Тяговые электрические машины и преобразователи: Методическое руководство к курсовому проектированию по дисциплине «Тяговые электрические машины и преобразователи» - УрГУПС, 2004 г.
2 Проектирование тяговых электрических машин.: Учеб. пособие для вузов ж.-д. трансп. / Под ред. М.Д. Находкина. - М.: Транспорт, 1967. – 536 с.
3 Костенко МЛ., Пиотровский Л.М. Электрические машины.: Учебник для студентов высш. техн. учеб. заведений, Изд. 3-е, перераб. -Л.: Энергия, 1972.-544 с.
4 Захарченко Д.Д., Ротанов Н.А. Тяговые электрические машины.: Учеб. для вузов ж.д. трансп. - М.: Транспорт, 1991. - 343 с,
5 Алексеев А.Е. Тяговые электрические машины и преобразователи. - Л.: Энергия, 1977. - 445 с.
6 Уткин В.Г., Соколов С.И., Сукач Э.И. Электропоез ЭР2 руководство по эксплуатации.- М.: Транспорт, 1974.- 248с.
Похожие работы
... 5,75, а Z = 100 и z = 17. Централь передачи определяется по следующей формуле: (27) Подставляя численные значения, получаем: 1.7 Определение габаритных размеров Длина тягового электродвигателя ограничивается расстоянием между внутренними гранями колесных пар, которое для железных дорог равно 1,44 м. Однако здесь же ...
... превышения температур обмоток . Должно выполниться условие: ; (9.5) 49.60<140 – условие действительно выполняется. Вывод: тяговые двигатели данного локомотива с массой поезда Q=4900 т на участке длиной 19.88 км не перегреваются.10. Расчёт расхода топлива тепловозами на тягу поездов Затраты на электроэнергию или топливо являются ...
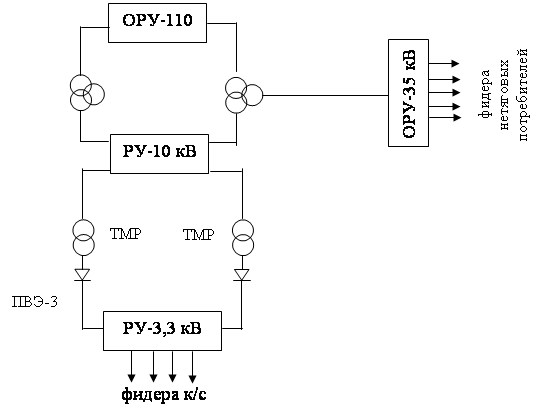
... аварийного режима к.з. 1.2 Структурная схема тяговой подстанции Долбина В данном дипломном проекте предлагается рассмотреть модернизацию тяговой промежуточной подстанции с питающим напряжением 110 кВ. В Белгородской дистанции электроснабжения имеется 9 тяговых подстанций постоянного тока, 8 из которых питаются от ЛЭП-110 кВ, в том числе и тяговая подстанция «Долбина». Тяговая подстанция ...
... 5 V 0 5 10 15 20 25 yк 0,30 0,272 0,251 0,236 0,223 0,213 Fк.сц 432,6 392,2 361,9 340 321,6 307,2 4.4 Построение тягово-энергетических характеристик тепловоза 2ТЭ121 На основании сводной таблицы (табл.3), полученной на основании расчётов на ПЭВМ в Math Cad строится тяговая характеристика тепловоза (рис.3). Тяговая характеристика тепловоза включает: 1) линии ...


0 комментариев