Опис конструкції шнекової фрези

1.3 Опис конструкції шнекової фрези

Шнекові фрези - зуборізальний інструмент, що працює методом обкочування, їх використовують для обробки прямозубих, косозубих і шевронних циліндричних коліс,а також для нарізання зубів черв’ячних коліс з різними видами зачеплення. Черв’ячна фреза як інструмент виходить з черв’яка шляхом прорізання канавок,утворюючих передню поверхню зубців і простір для розміщення стружки і затилування зубів і утворення задніх кутів по всьому контуру.

По конструктивному виконанні черв’ячні фрези бувають цілі, насадні і збірні.

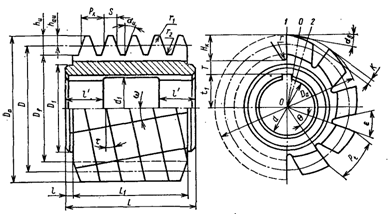
Рис. 1.3. Черв’ячна фреза. Конструктивні параметри

По виду обробки діляться на чорнові, чистові і прецензійні. По виду вихідного черв’яка,покладеного в основу черв’ячної фрези вони бувають евольвентні, Архімедові і конволютні для нарізання коліс з евольвентним зачепленням.

Для нарізання зубчастих коліс з циклоїдним зачепленням і зачепленням Новикова використовують фрези ,в основу яких покладені відповідні черв’яки.

Черв’ячні фрези працюють на спеціальних зубофрезерних станках. В процесі фрезерування фреза і заготовка обертається навколо своєї осі. За один оберт фрези заготовка обернеться на 1/Zk при одно західній фрезі і на a/ Zk якщо фреза багато західна; Zk – число зубців нарізуваного колеса,а – число заходів фрези.

Метод фрезерування черв’ячними фрезами є високопродуктивним і універсальним,дістав широке поширення у всіх видах виробництва для обробки циліндричних і черв’ячних коліс. На відміну від дискових і пальцевих фрез одна черв’ячна фреза може обробляти колеса з любим числом зубців даного модуля.

Основними конструктивними параметрами черв’ячної фрези є зовнішній діаметр - da0 ,довжина – L,діаметр отвору під оправку - d₁ ,число зубців z, форма і напрям канавок, розміри профілю зубців.

2. Моделювання. Загальні відомості

Моделюванням називається дослід який проводиться на моделях чи на реальних установках з використанням методів теорії подібності при постановці і обробці результатів експеремента. Подібними називаються явища, у яких всі процеси (повна схожість) чи найбільш суттєве при даному дослідженні (неповна чи локальна схожість)в любий момент часу и в довільній точці простору і одрізняються від відповідних параметрів іншого явища в певне (постійне) число раз, яке називається масштабом.

Ознаками схожості і умовами встановлення її при реалізації моделювання служать численно одинакові критерії схожості.

Подібність може бути фізичною і математичною. У фізичних подібних явищах всі процеси (основні для даного досліду)мають однакову фізичну природу, але описуються однаковими рівняннями. Можливість встановлення схожості при моделюванні реалізують з допомогою теорії подібності, яка ґрунтується на аналізі рівнянь.

Під моделями розуміють установки, пристрої, комбінації окремих елементів чи суму логічних представлень, які відтворюють явища чи групи явищ, подібних до вивчаючих. Моделі ділять на наступні основні групи:

·          Математичні моделі, призначені для дослідження явищ на установках,які дозволяють реалізувати математичну схожість;

·          Геометричні моделі чи макети, дають тільки геометричну схожість без відтворення природи явища що проходить;

·          Фізичні моделі – для дослідження явищ на установках, які зберігають схожість основних фізичних процесів досліджуваного явища.

При фізичному і математичному моделюванні виникають похибки трьох видів:

1.         Первинна похибка через проходження між справжнім значенням фізичної величини і її розрахунковим значенням, прийнятим для здійснення на моделі;

2.         Друга похибка - через неточність відтворення на моделі модельованих величин (розрахункових значень) і похибок, зв’язаних з розмірами;

3.         Принципова похибка – через неповного врахування в моделі факторів які заздалегідь впливають на вивчаючі процеси (наприклад, обумовленим моделюванням замість точного).

В інструментальному виробництві фізичне і математичне моделювання використовується для того,щоб наперед оцінити ефективність нових конструкцій ріжучого інструменту і визначити оптимальні параметри,які забезпечать максимальну стійкість.

Різальні властивості любого інструменту визначаються в процесі різання на основі порівняння результатів цього процесу з якими-небудь іншими показниками. Фізичне моделювання дає можливість замінити складний різальний інструмент більш простим і розглядати замість реального процесу роботи складного інструмента на більш простий. Можливі і інші способи фізичного моделювання процесу.

Математичним моделюванням можна визначити ефективність нової конструкції інструмента до його виготовлення. Крім цього кореляційне рівняння залежності стійкості від деяких параметрів інструмента і умов різання також можна використати як математичні моделі роботи різальних інструментів. Ці рівняння прораховують на ЄВМ і визначають оптимальну комбінацію параметрів які забезпечують необхідну стійкість інструменту.

Любу модель можна оцінити тільки на основі встановлення тісного кореляційного зв’язку між результатами роботи реального інструменту в звичайних виробничих умовах і результатами ,які отримані при моделюванні.

Для оцінки моделі можна використовувати коефіцієнт кореляції. Якщо X1 i X2 випадкові величини,взяті фіксовані моменти часу t1 i t2 то коефіцієнт кореляції.

Де М – символ математичного очікування;

D – символ дисперсії;

Коефіцієнт кореляції є мірою залежності випадкових величин X1 i X2.В випадку незалежності цих величин r = 0.Якщо X1 i X2 зв’язані точною лінійною залежністю, то r=±1. Відповідно,величини X1 i X2 будуть некорильовані, якщо r = 0,и корельовані, якщо .