Навигация
Работа асинхронного двигателя под нагрузкой
1.4 Работа асинхронного двигателя под нагрузкой
n1 – частота вращения магнитного поля статора. n2 – частота вращения ротора.
n1 >n2
Магнитное поле статора вращается в том же направлении, что и ротор и скользит относительно ротора с частотой ns= n1 – n2
Отставание ротора от вращающегося магнитного поля статора характеризуется скольжением S= ns / n1, => S =(n1 – n2) / n1
Если ротор неподвижен, то n2=0, S=(n1 – n2) / n1, => S = n1 / n1=1
Если ротор вращается синхронно с магнитным полем, то скольжение S= 0.
При холостом ходе, то есть при отсутствии нагрузки на валу двигателя скольжение ничтожно мало и его можно принять равным 0. Нагрузкой на валу ротора может служить, например резец токарного станка. Он создаёт тормозной момент. При равенстве вращающего и тормозного момента двигатель будет работать устойчиво. Если нагрузка на валу увеличилась, то тормозной момент станет больше вращающего и частота вращения ротора n2 уменьшится. Согласно формуле S =(n1 – n2) / n1 скольжение увеличится. Так как магнитное поле статора скользит относительно ротора с частотой ns= n1 – n2, то оно будет пересекать проводники ротора чаще, в них увеличится ток и двигательный вращающий момент, который вскоре станет равным тормозному. При уменьшении нагрузки, тормозной момент становится меньше вращающего, увеличивается n2 и уменьшается S. Уменьшается Э.Д.С и ток ротора и вращающий момент вновь равен тормозному. Магнитный поток в воздушном зазоре машины при любом изменении нагрузки остаётся примерно постоянным.
2. Рабочие характеристики асинхронного двигателя
Рабочие характеристики асинхронного двигателя есть зависимость
S – скольжения
n2 – частоты вращения ротора
М – развиваемого момента
I1-потребляемого тока
Р1-расходуемой мощности
СОSφ-коэффициента мощности
КПДη
От полезной мощности Р2 на валу машины.
Эти характеристики снимаются при естественных условиях. Частота тока f1 и напряжение U1 остаются постоянными. Изменяется только нагрузка на валу двигателя.
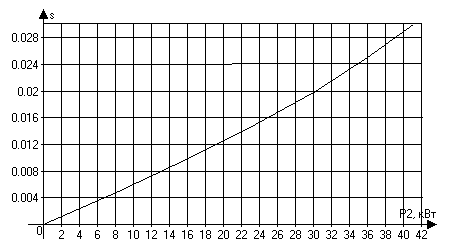
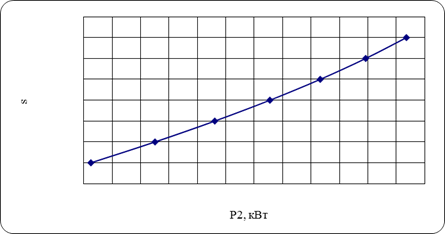
При увеличении нагрузки на валу двигателя S увеличивается. При холостом ходе двигателя n2≈n1, и S≈0. При номинальной нагрузке скольжение обычно составляет от 3 до 5%.
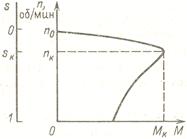
При увеличении нагрузки на валу двигателя частота вращения n2 уменьшается. Однако, изменение частоты вращения при увеличении нагрузки от 0 до номинальной очень незначительны и не превышают 5%. Поэтому, скоростная характеристика асинхронного двигателя является жёсткой. Кривая имеет очень малый наклон к горизонтальной оси.
Вращающий момент М, развиваемый двигателем, уравновешен тормозным моментом на валу Мт и моментом М0, идущим на преодоление механических потерь, то есть М= Мт + М0 =Р2/Ω2+ М0, где Р2 – полезная мощность двигателя, Ω2-угловая скорость ротора. При холостом ходе М= М0. С увеличением нагрузки вращающий момент также увеличивается, причём за счёт некоторого уменьшения частоты вращения ротора увеличение вращающего момента происходит быстрее, чем полезной мощности на валу.
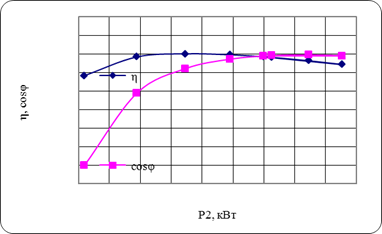
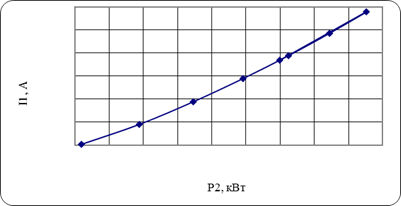
Ток I1, потребляемый двигателем из сети неравномерно изменяется с увеличением нагрузки на валу двигателя. При холостом ходе СОSφ-коэффициента мощности – мал. И ток имеет большую реактивную составляющую. При малых нагрузках на валу двигателя активная составляющая тока статора меньше реактивной составляющей, поэтому активная составляющая тока незначительно влияет на ток I1. При больших нагрузках активная составляющая тока статора становится больше реактивной и изменение нагрузки вызывает значительное изменение тока I1.
Графическая зависимость потребляемой двигателем мощности Р1 изображается почти прямой линией, незначительно отклоняющейся вверх при больших нагрузках, что объясняется увеличением потерь в обмотках статора и ротора с возрастанием нагрузки.
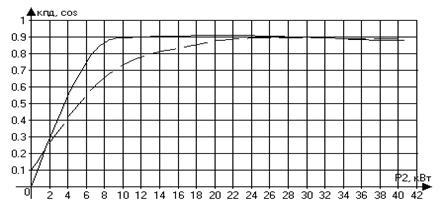
Зависимость СОSφ-коэффициента мощности – от нагрузки на валу двигателя следующая. При холостом ходе СОSφ мал, порядка 0,2. Так как активная составляющая тока статора, обусловленная потерями мощности в машине, мала по сравнению с реактивной составляющей этого тока, создающей магнитный поток. При увеличении нагрузки на валу СОSφ возрастает, достигая наибольшего значения 0,8–0,9, в результате увеличения активной составляющей тока статора. При очень больших нагрузках происходит некоторое уменьшение СОSφ, так как в следствие значительного увеличения скольжения и частоты тока в роторе возрастает реактивное сопротивление обмотки ротора.
Кривая КПДη имеет такой же вид как в любой машине или трансформаторе. При холостом ходе КПД=0. С увеличением нагрузки на валу двигателя КПД резко увеличивается, а затем уменьшается. Наибольшего значения КПД достигает при такой нагрузке, когда потери мощности в стали и механические потери, не зависящие от нагрузки, равны потери мощности в обмотках статора и ротора, зависящим от нагрузки.
Похожие работы
... также отвечает поставленным в техническом задании требованиям. Специальная часть. Проводниковые материалы и обмоточные провода, применяемые в асинхронных двигателях. Проводниковые материалы. К проводниковым материалам, применяемым в электромашиностроении, относятся медь и алюминий. Серебро, имеющее ...
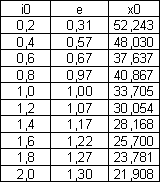
... Потери, не изменяющиеся при изменении скольжения : Pст. + Pмех. = 727,12+125,6 = 852,17 Вт. Таблица 1. Рабочие характеристики асинхронного двигателя. Параметр Ед-ца Скольжение 0,005 0,01 0,015 sн=0,019 0,02 0,025 0,03 a’×r’2/s Ом 48,53 24,27 16,18 12,77 12,13 9,71 8,09 b’×r’2/s Ом 0 0 0 0 0 0 0 R = a + a¢*r¢2/s Ом 49,04 ...
... 0,726 (Ом) 11) Индуктивное сопротивление двигателя, определяемое по пусковому режиму. (1.11) отсюда 12) Приведенное индуктивное сопротивление обмотки ротора (1.12) 2. Расчет механической характеристики асинхронного двигателя в двигательном режиме Особенностью работы АД в двигательном режиме является незначительное изменение скольжения двигателя на рабочей части ...
... 2,54 2,45 2,59 Графики пусковых характеристик спроектированного двигателя с короткозамкнутым ротором изображены на рисунке 6 и рисунке 7. Рисунок 6 – Зависимость Рисунок 7 – Зависимость Спроектированный асинхронный двигатель удовлетворяет требованиям ГОСТ как по энергетическим показателям (КПД и ), так и по пусковым характеристикам. 9. ТЕПЛОВОЙ РАСЧЁТ Превышение температуры ...


0 комментариев