Навигация
Масштабный коэффициент построения картины зацепления
1. Масштабный коэффициент построения картины зацепления.
![]()
Исходные данные:
Модуль ![]()
Частота вращения вала двигателя ![]()
Частота вращения кривошипа ![]()
Числа зубьев ![]()
Знак передаточного отношения - минус
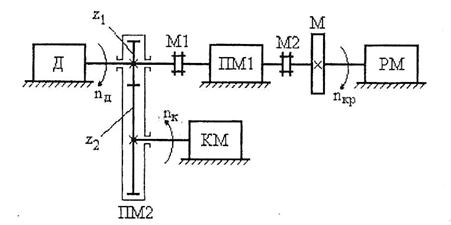
Номер схемы редуктора ![]() (рис.8).
(рис.8).
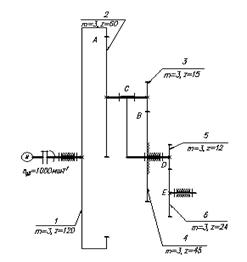
Рис.8 - Редуктор
Передаточное отношение простой передачи
![]()
Общее передаточное отношение редуктора
![]()
Передаточное отношение планетарной передачи
![]()
Формула Виллиса для планетарной передачи
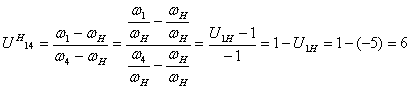
5. Передаточное отношение обращенного механизма, выраженное в числах зубьев.
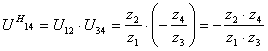
Представим полученное отношение в виде
![]()
6. Подбор чисел зубьев
Выбираем числа зубьев: ![]()
7. Условие соосности
![]()
Условие соосности выполнено
8. Делительные диаметры
![]()
![]() ,
, 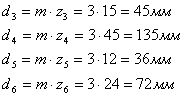
9. Угловая скорость вала двигателя
![]()
10. Линейная скорость точки A колеса z1
![]()
11. Масштабный коэффициент Kv
![]()
12. Масштабный коэффициент построения плана редуктора
![]()
1. Определение частот вращения аналитическим методом.
![]() откуда
откуда ![]()
Знак плюс показывает, что водило вращается в одном направлении с валом
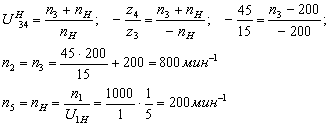
2. Определение частот вращения графическим методом.
Масштабный коэффициент плана частот вращения
![]()
Частоты вращения, полученные графическим способом.
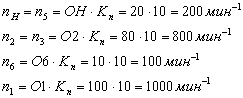
Определение погрешностей:
![]()
![]()
Private Sub CommandButtonl_Click ()
Dim zl, z2, m, ha, C, z5, z6, xl, x2, aw, a, h, hal, ha2, hfl, hf2, dl, d2, dal, da2, dBl, dB2, dfl, df2, SI, S2, P, PB, rf, q As Double zl=CDbl (TextBoxl. Value)
z2 = CDbl (TextBox2. Value) m = CDbl (TextBox3. Value)
ha = CDbl (TextBox4. Value) c = CDbl (TextBox5. Value)
q = CDbl (TextBox6. Value)
ListBoxl. Clear
ListBoxl. Addltem ("Начало отсчета")
ListBoxl. Addltem ("zl=" & zl)
ListBoxl. Addltem ("z2=" & z2)
ListBoxl. Addltem ("m=" & m)
ListBoxl. Addltem ("ha*=" & ha)
ListBoxl. Addltem ("C*=" & C) q = (q* 3.14) /180
ListBoxl. Addltem ("угол-' & q) xl= (17-zl) /17
ListBoxl. Addltem ("xl=" & xl) x2 = - xl
ListBoxl. Addltem ("x2=" & x2) a = m* (zl +z2) /2
ListBoxl. Addltem ("a=" & a) aw=a
ListBoxl. Addltem ("aw=" & aw) h=2.25*m
ListBoxl. Addltem ("h=" & h) ha1=m* (ha+x1)
ListBoxl. Addltem ("ha1=" &ha1) ha2=m* (ha+x2)
ListBoxl. Addltem ("ha2=" &ha2) hf1=m* (ha+c-x1)
ListBoxl. Addltem ("hf1=" &hf1) hf2=m* (ha+c-x2)
ListBoxl. Addltem ("hf2=" &hf2) d1=m*z1
ListBoxl. Addltem ("d1=" &d1) d2=m*z2
ListBoxl. Addltem ("d2=" &d2) dw1=d1
ListBoxl. Addltem ("dw1=" &dw1) dw2 = d2
ListBoxl. Addltem ("dw2=" & dw2) dal =dl +2*hal
ListBoxl. Addltem ("dal=" & dal) da2 - d2 + 2 * ha2
ListBoxLAddltem ("da2=" & da2) dfl = dl - 2 * hfl
ListBoxLAddltem ("dfl=" & dfl) df2 = d2-2*hf2
ListBoxLAddltem ("hf2=" & h£2) dBl=dl*Cos (q)
ListBoxLAddltem ("dBl=" & dBl) dB2 = d2 * Cos (q)
ListBoxLAddltem ("dB2=" & dB2) Sl=0.5*3.14*m + 2*xl * m * Tan (q)
ListBdxl. AddItem ("Sl="&Sl)
S2 = 0.5 * 3.14 *m + 2*x2*m* Tan (q) ListBoxLAddltem ("S2=" & S2)
P = 3.14*m
ListBoxLAddltem ("p=" & P)
pB = p * Cos (q)
ListBoxLAddltem ("pB=" & pB) rf = 0.38 * m
ListBoxLAddltem ("r£=" & rf) End Sub
Private Sub CommandButton2_Click () UserForm 1. Hide
End Sub
Исходные данные
Угол зацепления а = 20
Коэффициент высоты головки зубаha = l
Коэффициент радиального зазора С = 0,25 Модуль m = 3 мм
Число зубьев шестерни z 1 = 12
Число зубьев колеса z2 = 24
Результаты расчета
Начальное межосевое расстояние aw = 54 мм
Высота зуба h = 6,67 мм
ШЕСТЕРНЯКОЛЕСО
Коэффициент смещенияХ1 = 0,29Х2= - 0,29
Высота головки зуба hal= 3,87 ммha2=2,13 мм
Высота ножки зуба hfl = 2,88 ммhf2=4,62 мм
Делительный диаметр dl= 36 ммd2=72мм
Начальный диаметр dwl= dl= 36 ммdw2=72 мм
Диаметр вершин dal=43,74 ммda2 =76,26 мм
Диаметр впадин dfl=30,24 мм df2 =62,76 мм
Основной диаметр dBl=33,83 ммdB2 =67,66 мм
Толщина зуба S 1= 5,34 ммS2 =4,074 мм
Шаг Р=9,42 мм
Основной шаг Рв=8,85 мм
Радиус rf=l,14 мм
4. Синтез и анализ кулачкового механизма
Исходные данные:
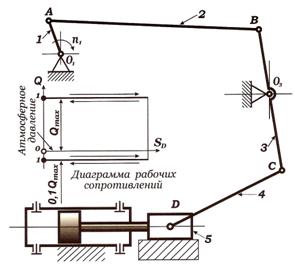
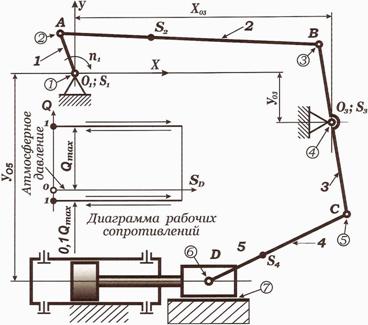
а) диаграмма движения выходного звена
![]()
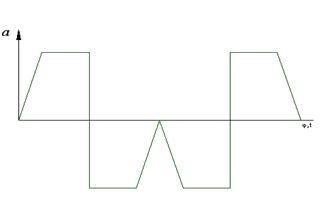
б) частота вращения кривошипа ![]()
в) максимальный подъем толкателя ![]()
г) рабочий угол кулачка ![]()
д) угол давления ![]()
ж) дезаксиал кулачка ![]()
з) роликовый тип кулачкового механизма (рис 9)
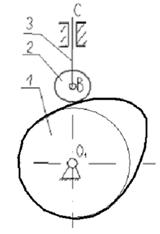
Рис.9 - Роликовый тип кулачка
4.1 Диаграмма движения толкателя
По заданному графику ускорения толкателя а = f (t), графическим интегрированием по методу хорд получаю графики скорости и перемещения толкателя.
База интегрирования:
![]()
Графики V (s), a (s) получаю методом исключения общего переменного параметра t - время.
Масштабный коэффициент перемещения.
![]()
где ![]() -максимальное значение ординаты графика, соответствует заданному подъему толкателя.
-максимальное значение ординаты графика, соответствует заданному подъему толкателя.
![]()
где ![]() - частота вращения кулачка:
- частота вращения кулачка: ![]()
![]() =120 мм - длина отрезка на оси абсцисс графика изображающая время поворота кулачка на рабочий угол.
=120 мм - длина отрезка на оси абсцисс графика изображающая время поворота кулачка на рабочий угол.
![]()
Масштабный коэффициент скорости толкателя.
![]()
![]()
Выбор минимального радиуса кулачка.
Минимальный радиус кулачка выбираю из условия заданного угла давления ![]() .
.
Для этого строю совместный график ![]() . На этом графике текущее перемещение
. На этом графике текущее перемещение![]() откладываю вдоль оси координат в стандартном масштабе
откладываю вдоль оси координат в стандартном масштабе ![]() . К полученному графику провожу две касательные под углом давления
. К полученному графику провожу две касательные под углом давления ![]() .
.
Точка пересечения касательных образует зону выбора центров вращения кулачка, соединив выбранную точку с началом графика, получаю значение минимального радиус кулачка.
Аналоги скорости рассчитываем в стандартном масштабе следующим образом.
![]() ,
, 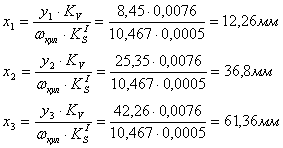
Значение минимального радиуса центрового профиля кулачка с графика S’ (![]() )
)
![]()
![]()
Радиус ролика
rP = (0.2÷ 0.4) ![]() ; rP =
; rP =![]() = 0,018 м
= 0,018 м
Минимальный радиус действительного кулачка
![]()
![]()
Построение профиля кулачка.
Построение профиля кулачка произвожу методом обращенного движения. Масштабный коэффициент построения![]() .
.
В выбранном масштабе строю окружность радиусом ![]() = 60 мм.
= 60 мм.
Откладываю фазовый рабочий угол ![]() . Делю этот угол на столько частей, сколько на графике. Через точки деления провожу оси толкателя во вращенном движении. Для этого соединяю точку деления с центром вращения кулачка. Вдоль осей толкателя от окружности минимального радиуса откладываю текущее перемещение толкателя в выбранном масштабе.
. Делю этот угол на столько частей, сколько на графике. Через точки деления провожу оси толкателя во вращенном движении. Для этого соединяю точку деления с центром вращения кулачка. Вдоль осей толкателя от окружности минимального радиуса откладываю текущее перемещение толкателя в выбранном масштабе.
Соединив полученные точки, имеем центровой профиль кулачка. Обкатывая ролик по центровому профилю во внутрь, получаю действительный профиль кулачка.
4.4 Максимальные значения скорости, ускорения толкателя
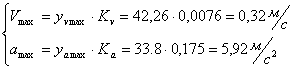
Public Sub kul ()
Dim I As Integer
Dim dis1, dis2, R, a1, a2, arksin1, arksin2, BETTA, BET As Single
Dim R0, FIR, FI0, FII, SHAG, E As Single
Dim S (1 To 36) As Single
R0 = InputBox ("ВВЕДИТЕ МИНИМАЛЬНЫЙ РАДИУС КУЛАЧКА RO")
FIR = InputBox ("ВВЕДИТЕ РАБОЧИЙ УГОЛ КУЛАЧКА FIR")
FI0 = InputBox ("ВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ УГЛА ПОВОРОТА КУЛАЧКА FI0")
E = InputBox ("ВВЕДИТЕ ДЕЗАКСИАЛ E")
For I = 1 To 36
S (I) = InputBox ("ВВЕДИТЕ СТРОКУ ПЕРЕМЕЩЕНИЙ S (" & I & ")")
Next I
FIR = FIR * 0.0174532
SHAG = FIR / 12
FI0 = FI0 * 0.0174532
FII = FI0
For I = 1 To 36
dis1 = (R0 ^ 2 - E ^ 2) ^ (1/2)
dis2 = S (I) ^ 2 + R0 ^ 2 + 2 * S (I) * dis1
R = dis2 ^ (1/2)
a1 = E / R
a2 = E / R0
arksin1 = Atn (a1/ (1 - a1 ^ 2) ^ (1/2))
arksin2 = Atn (a1/ (1 - a2 ^ 2) ^ (1/2))
BETTA = FII + arksin1 - arksin2
BETTA = BETTA * 180/3.1415
Worksheets (1). Cells (I,
1) = R
Worksheets (1). Cells (I,
2) = BETTA
FII = FII + SHAG
Next I
End Sub
Таблица 4.1 - Результаты расчета
| R, мм | BETTA | R, мм | BETTA | R, мм | BETTA | R, мм | BETTA |
| 42 | 0 | 56.64 | 104 | 42 | 208 | 42 | 312 |
| 42.7 | 13 | 51.06 | 117 | 42 | 221 | 42 | 325 |
| 45.48 | 26 | 45.48 | 130 | 42 | 234 | 42 | 338 |
| 51.06 | 39 | 42.7 | 143 | 42 | 247 | 42 | 351 |
| 56.64 | 52 | 42 | 156 | 42 | 260 | ||
| 59.44 | 65 | 42 | 169 | 42 | 2731 | ||
| 60.12 | 78 | 42 | 182 | 42 | 286 | ||
| 59.64 | 91 | 42 | 195 | 42 | 299 |
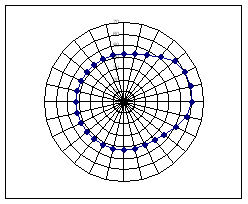
Рис.10 - Схема кулачка.
Список использованных источников
1. Артоболевский И.И. Технология машин и механизмов. М.: Наука, 1998. -720с.
2. Кожевников С.И. Технология машин и механизмов. М.: Машиностроение, 1989. - 583с.
3. Кореняко А.С. Курсовое проектирование по технологии машин и механизмов. Киев, Вища школа, 1970. - 330с.
4. Машков А.А. Технология машин и механизмов. Мн.: Высшая школа, 1967. - 469с.
5. Филонов И.П. Технология машин и механизмов. Мн.: Дизайн ПРО, 1998. - 428с.
6. Фролов К.В. Технология машин и механизмов. М.: Высшая школа, 1998. - 494с.
Похожие работы
... этого отрезка в миллиметрах вычислим момент инерции маховика. Углы вычисляем по формулам: Проводим вычисления и находим: Проводим касательные и измеряем длину отрезка KL. 3. Динамический анализ рычажного механизма 3.1 Построение планов скоростей и ускорений в заданном положении Вычертим кинематическую схему механизма в заданном положении градусов. При построении ...
... ,5 – 174,5 90 Δ, % 0,00 0,00 0,00 0,00 0,00 0,00 0,00 ПРИВЕДЁННЫЕ ФАКТОРЫ Положение 2 Расчёт ЭВМ Погрешность Δ, % – 156,6 – 156,6 0,00 IПР 0,22 0,22 0,00 2. Синтез и анализ кулачкового механизма 2.1 Построение диаграмм движения толкателя 1. Строится заданная диаграмма ускорений толкателя. Максимальная ордината ...
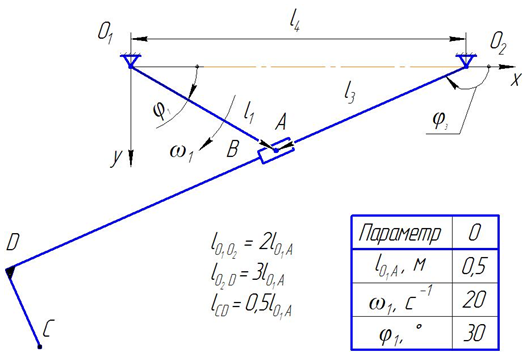
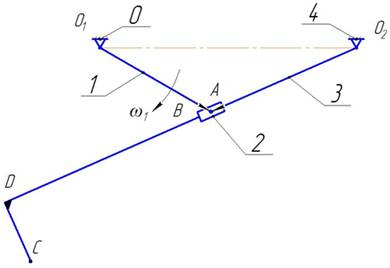
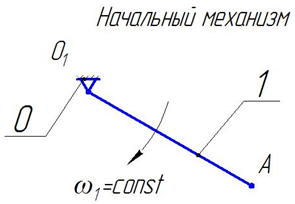
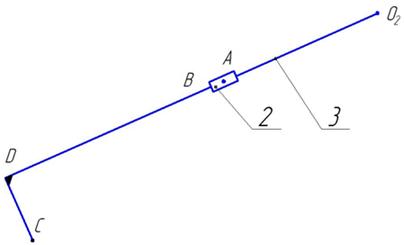
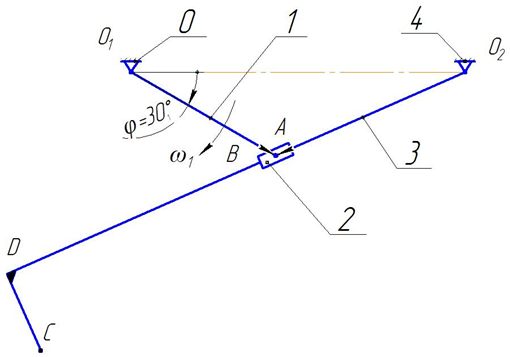
... [lCD]: Методом засечек в принятом масштабе µ строим план положения механизма для заданного положения кривошипа О1А, φ1 = 30° (рис. 5). Рис. 5 План положения механизма, µ = 0,01 м/мм 3. Кинематический анализ рычажного механизма Построение плана скоростей. План скоростей строим для заданного положения механизма, для φ1 = 30° (рис. 5). Построение плана скоростей начинаем ...
... 2.7 Определение кинетической энергии и приведенного момента инерции механизма Кинетическая энергия механизма равна сумме кинетической энергии звеньев: Тмех=∑Тi Для механизма насоса с заданными параметрами кинетическая энергия звена равна: ∑Тi=Т3+Т5= Где JO2’==12·0,352/3=0,49 кг·м2 JO2’’==30·0,1552/3=0,24 кг·м2 Т3=(0,49+0,24)·4,942/2=8,9 ...
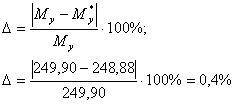
0 комментариев