Контрольная операция

1 контрольная операция

Таблица №13

№ инт.	Диапазон значений измеряемой величины в интервале		Вероятность P*i	Вероятность Pi	Среднее квадратическое отклонение	Математическое ожидание
1	4,65014364	4,86106248	0,15	0,03	0,16	5,02
2	4,86106248	5,07198132	0,46	0,92
3	5,07198132	5,28290016	0,33	0
4	5,28290016	5,493819	0,05	0,03
5	5,493819	5,70473784	0	0
6	5,70473784	5,91565668	0	0,01
7	5,91565668	6,12658548	0	0,01

Используя функцию Лапласа определяем теоретические вероятности.

Находим суммарную вероятность:

k – число интервалов разбиения в данном случае k=7.

Определяем величину расхождения.

По таблице 8 методического пособия находим, что полученное по данным выборки значение значениеменьше значения , соответствующего 0.1% уровню значимости (число степеней свободы r=k-3=7-3=4), другими словами вероятность получить такие же или еще большие значения  при нашей гипотезе менее 0.1%, отсюда заключаем, что отклонения являются значительными, и гипотеза о нормальной совокупности, на которой получена наша выборка, противоречит наблюдениям

Таблица №14

№ инт.	Диапазон значений измеряемой величины в интервале		Вероятность P*i	Вероятность Pi	Среднее квадратическое отклонение	Математическое ожидание
1	16387,6289	17918,0945	0,29	0,05	944,59	18388,80
2	17918,0945	19448,5602	0,57	0,94
3	19448,5602	20979,0259	0,07	0
4	20979,0259	22509,4916	0,05	0
5	22509,4916	24039,9573	0	0
6	24039,9573	25570,4229	0	0
7	25570,4229	27100,8886	0	0,01

Используя функцию Лапласа определяем теоретические вероятности.

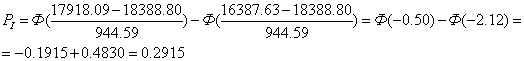
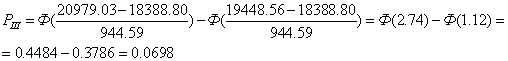
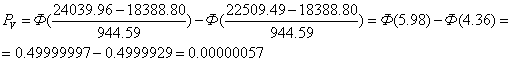
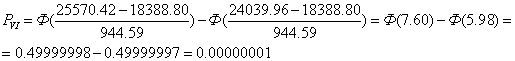
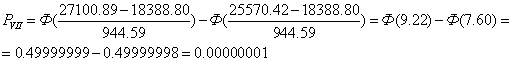
Находим суммарную вероятность:

k – число интервалов разбиения в данном случае k=7.

Определяем величину расхождения.

По таблице 8 методического пособия находим, что полученное по данным выборки значение значениеменьше значения , соответствующего 0.1% уровню значимости (число степеней свободы r=k-3=7-3=4), другими словами вероятность получить такие же или еще большие значения  при нашей гипотезе менее 0.1%, отсюда заключаем, что отклонения являются значительными, и гипотеза о нормальной совокупности, на которой получена наша выборка, противоречит наблюдениям

Таблица №15

№ инт.	Диапазон значений измеряемой величины в интервале		Вероятность P*i	Вероятность Pi	Среднее квадратическое отклонение	Математическое ожидание
1	8,2797248	9,60626877	0,0174	0,05	1,46	12,66
2	9,60626877	10,9328124	0,0982	0,03
3	10,9328127	12,2593567	0,2766	0,14
4	12,2593567	13,5859006	0,3453	0,59
5	13,5859006	14,9124446	0,1993	0,13
6	14,9124446	16,2389886	0,0546	0,03
7	16,23898862	17,5655426	0,0068	0,03

Используя функцию Лапласа определяем теоретические вероятности.

Находим суммарную вероятность:

k – число интервалов разбиения в данном случае k=7.

Определяем величину расхождения.

По таблице 8 методического пособия находим, что полученное по данным выборки значение значениеменьше значения , соответствующего 98% уровню значимости (число степеней свободы r=k-3=7-3=4), другими словами вероятность получить такие же или еще большие значения  при нашей гипотезе более 98%, отсюда заключаем, что отклонения нельзя считать значительными, и гипотеза о нормальной совокупности, на которой получена наша выборка, не противоречит наблюдениям

Таблица №16

№ инт.	Диапазон значений измеряемой величины в интервале		Вероятность P*i	Вероятность Pi	Среднее квадратическое отклонение	Математическое ожидание
1	136,434331	168,124257	0,0483	0,1	37,77	228,08
2	168,124257	199,814183	0,1707	0,13
3	199,814183	231,504109	0,3093	0,15
4	231,504109	263,194036	0,2879	0,54
5	263,194036	294,883962	0,1378	0,06
6	294,883962	326,573888	0,0338	0,01
7	326,573888	358,263824	0,0043	0,01

Используя функцию Лапласа определяем теоретические вероятности.

Находим суммарную вероятность:

k – число интервалов разбиения в данном случае k=7.

Определяем величину расхождения.

По таблице 8 методического пособия находим, что полученное по данным выборки значение значениеравно значению , соответствующего 98% уровню значимости (число степеней свободы r=k-3=7-3=4), другими словами вероятность получить такие же или еще большие значения  при нашей гипотезе более 98%, отсюда заключаем, что отклонения нельзя считать значительными, и гипотеза о нормальной совокупности, на которой получена наша выборка, не противоречит наблюдениям

Оценка состояния ТП

Контроль осуществляется с помощью КК Шухарта (Контрольные карты по количественному признаку).