Розрахунок похибки вимірювання кутової швидкості

7.2 Розрахунок похибки вимірювання кутової швидкості

Для визначення кутової швидкості необхідно диференціювати вихідний сигнал ТП. В загальному випадку результуюча похибка дискретного вимірювання кутової швидкості має наступні складові [16]: методична похибка; похибка інтерполяції; похибка, що обумовлена похибкою одного відліку АЦП; похибка, що обумовлена випадковими завадами та неточністю виконання модулятору та діафрагми.

Методична похибка дискретного вимірювання кутової швидкості в момент t_i визначається виразом:

, (7.7)

де  - час між відліками вихідного сигналу ТП;

 - значення кута повороту в моменти часу  та .

У випадку, коли кутове прискорення дорівнює нулю (кутова швидкість постійна), методична похибка відсутня. Для оцінки методичної похибки використаємо методику, що застосовано у [16]. Припустимо, що усі інші похибки, окрім методичної, відсутні. Вважаємо вихідний сигнал ТП гладкою функцією часу, яка у любій точці розкладається у ряд Тейлора. Якщо розкласти  біля точки  в ряд Тейлора, обмежившись трьома членами ряду, отримуємо:

, (7.8)

де  - точка між  та . Після нескладних перетворень отримуємо:

. (7.9)

Максимальна оцінка методичної похибки вимірювання кутової швидкості:

, (7.10)

де  - максимальне значення другої похідної вихідного сигналу ТП на інтервалі диференціювання, виражене у одиницях кутового прискорення. Значення  обумовлене не тільки режимом роботи об’єкту контролю, а й імпульсними завадами у вихідному сигналі ТП:

 , (7.11)

де - коефіцієнт, який зворотно пропорційний крутизні залежності вихідної напруги ТП від кута повороту.

Цей коефіцієнт дорівнює:

. (7.12)

Провівши аналогічні перетворення, можна довести, що методична похибка на початку інтервалу диференціювання дорівнює методичній похибки на кінці інтервалу. Якщо виникає необхідність подальшої обробки даних, тобто запізнення вимірювальної інформації не важливе, можна визначити методичну похибку із запізненням на . В цьому випадку, у відповідності з [16]:

. (7.13)

Цю оцінку можливо використовувати при обробці даних вимірювання з використанням інтерполяції. Вище наведені розрахунки справедливі тільки для диференціаторів першого типу. Для диференціаторів другого типу, у відповідності з [16], оцінка максимальної методичної похибки має вигляд:

, (7.14)

а для диференціатору третього типу:

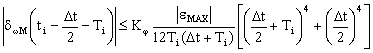. (7.15)

Диференціатори другого та третього типу мають більш високу завадостійкість, ніж диференціатор першого типу. Але вони мають більший інтервал диференціювання. Максимальна оцінка методичної похибки диференціатору першого типу прямо пропорційна максимальному значенню другої похідної вихідної напруги ТП та часу Т_В. Значення другої похідної вихідної напруги в загальному випадку є випадковою величиною, яка залежить від багатьох факторів. На неї впливають кутове прискорення, випадкові завади, резонансні явища, що обумовлені муфтою спряження, співвідношення моментів на валу, прецесія та нутація ротору, неточність виконання прорізів модулятору та діафрагми та інше. У роботі [18] доведено, що якщо виходити з режиму роботи об’єкту контролю з максимальними динамічними моментами (максимальне навантаження, максимальна швидкодія), закон розподілу максимального кутового прискорення буде наближатись до дискретного двомодального. У цьому випадку, закон розподілу методичної похибки диференціатору першого типу, має також дискретний двомодальний закон розподілу:

. (7.16)

Середньоквадратичне відхилення методичної похибки:

. (7.17)

Для вимірювання швидкісних діаграм та проведення динамічних вимірювань кутової швидкості необхідно знаходити виміряні значення між точками опитування. Для цього використовують інтерполяцію. При цьому виникає похибка інтерполяції. Оцінки інтерполяції розглянуто у [12]. Так стосовно до диференціатора першого типу похибка східчастої інтерполяції оцінюється виразом:

. (7.18)

При використанні лінійної інтерполяції оцінка похибки має вигляд:

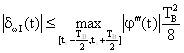. (7.19)

При використанні інтерполяції кубічними сплайнами, можна використовувати точні або асимптотично точні оцінки похибок сплайн-інтерполяції на класах функцій [13]. Всі вони достатньо складні для використання, тому в даному випадку доречно обмежитись тільки порядковими оцінками похибок. Якщо функція  належить класу  функцій, неперервних на  і, що мають неперервні похідні до k - того порядку (k = 0, 1, 2, 3, 4), то для похибки інтерполяції кубічним сплайном s(t) функції та її похідних дійсні оцінки:

 (7.20)

де с - невід’ємна константа;

. (7.21)

N_s - число відліків. Для функції  порядок наближення  сплайном s(t) дорівнює , порядок наближення похідної , дорівнює  та буде складати малу величину у порівнянні з іншими похибками.

Розглянемо похибку визначення кутової швидкості, що обумовлена похибкою квантування вихідного сигналу ТП. Припустимо, що методична похибка визначення кутової швидкості та похибка визначення кута повороту, що обумовлена неточністю виконання модулятору та діафрагми відсутні. Тоді результат вимірювання можливо записати у вигляді:

, (7.22)

де  - виміряне значення кутової швидкості у момент часу ;

,  - значення кута повороту у моменти часу  та ;

,  - похибка вимірювання кута повороту, що обумовлена квантуванням вихідного сигналу ТП, у моменти часу  та .

Друга частина виразу (7.22) є похибкою вимірювання кутової швидкості, що виникає внаслідок наявності похибки квантування вихідного сигналу ТП:

. (7.23)

Є очевидним, що закон розподілу похибки вимірювання кутової швидкості, що обумовлена похибкою квантування можна визначити як композицію законів розподілу величин  та , які як і похибка квантування мають рівномірний закон розподілу. При умові стаціонарності випадкових процесів, що обумовлюють виникнення цих похибок, їх закони розподілу можна вважати однаковими:

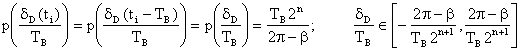. (7.24)

У відповідності з [19] композиція двох однакових прямокутних законів є трикутний закон (розподіл Сімпсона). Закон розподілу похибки вимірювання кутової швидкості, що обумовлена квантуванням вихідного сигналу ТП [14]:

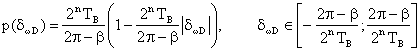. (7.25)

Середньоквадратичне значення цієї похибки:

. (7.26)

Випадкова похибка вимірювання кутової швидкості виникає під впливом випадкових завад та неточності виконання прорізів модулятору та діафрагми. Будемо вважати заваду на вході диференціатору першого типу стаціонарною випадковою функцією. Припустимо, що методична похибка визначення кутової швидкості та похибка квантування відсутні. Тоді результат вимірювання кутової швидкості можливо записати у вигляді:

. (7.27)

Друга частина виразу (7.27) є похибкою вимірювання кутової швидкості, що виникає внаслідок наявності похибки квантування вихідного сигналу ТП:

. (7.28)

Визначимо закон розподілу похибки вимірювання кутової швидкості, що обумовлена неточністю виконання модулятору та випадковими завадами. Цей закон можна визначити як композицію законів розподілу випадкових величин  та , які мають нормальний закон розподілу. При умові стаціонарності випадкових процесів, що обумовлюють виникнення цих похибок, їх закони розподілу можна вважати однаковими:

. (7.29)

У відповідності з [10] композиція двох однакових нормальних законів є також нормальним законом, який визначається виразом:

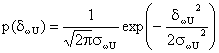. (7.30)

В силу властивостей стаціонарності [15], середньоквадратичне значення похибки вимірювання кутової швидкості, що обумовлена випадковими завадами та неточністю виконання модулятору та діафрагми:

. (7.31)

Середньоквадратичне відхилення загальної похибки вимірювання кутової швидкості знаходиться з виразу:

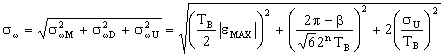. (7.32)

Графік відносного середньоквадратичного значення похибки вимірювання кутової швидкості  при різних значеннях , без урахування складової, що обумовлена неточністю виконання прорізів модулятору та діафрагми, при рад/с², n=12 наведено на рисунку 7.1.

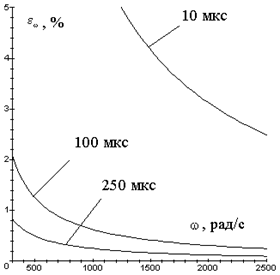
Рисунок 7.1 - Відносна середньоквадратична похибка вимірювання кутової швидкості.

Функція (7.26) має мінімум за аргументом Т_В, при якому результуюча середньоквадратична похибка вимірювання кутової швидкості мінімальна:

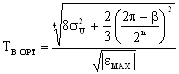. (7.33)

Враховуючи, що , вираз (7.33) можна записати як:

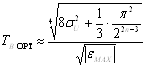. (7.34)

У випадку, коли похибкою, що обумовлена завадами та неточністю виконання модулятору та діафрагми можна знехтувати, вираз (7.34) прийме вигляд:

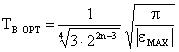. (7.35)

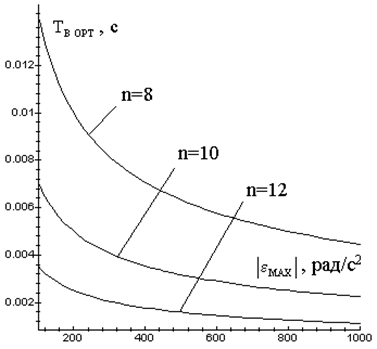
Залежності  від значення максимального кутового прискорення об’єкту контролю при різній розрядності АЦП наведено на рисунку 7.2.

Мінімальна відносна середньоквадратична похибка вимірювання кутової швидкості при відсутності випадкових завад визначається виразом:

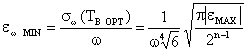. (7.36)

Графіки залежності цієї похибки від кутової швидкості при різній розрядності АЦП при рад/с наведено на рисунку 7.3. Їх наведено в діапазоні кутових швидкостей, в якому період дискретизації як мінімум у два рази менше за період вихідного сигналу ТП.

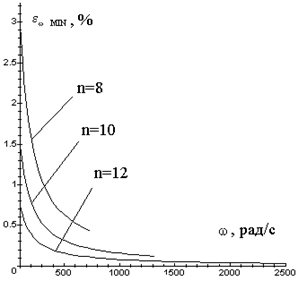
Рисунок 7.3 - Мінімальна відносна похибка вимірювання кутової швидкості

З аналізу рисунка 7.3. випливає, що в області низьких кутових швидкостей відносна середньоквадратична похибка вимірювання значно збільшується, що в першу чергу обумовлено похибкою квантування вихідного сигналу ТП.