Навигация
Уточнение вида зависимости
27904
знака
0
таблиц
0
изображений
2. Уточнение вида зависимости
Далее будут приведены некоторые определения и то, что из них следует для большей определенности функции привлекательности.
Математически в предположении о совпадении часть, касающаяся пропорциональности изменения условий dxs и dys, означает, что
dxs=
dys "s (2.1)
где через ‘обозначено дифференцирование.
Из справедливости гипотезы 2, т. е. из неизменности интенсивностей перехода при выполнении (2.1), следует, что функции предпочтения для аргументов с индексом s удовлетворяют уравнениям
,"s, (2.2)
где индекс s у функций j» и y» появился из-за того, что коэффициенты пропорциональности в гипотезе 2 могут быть разными для разных условий, т. е. зависеть от самого условия, следовательно, и от его номера s. Разные функции f и y подчеркивают лишь то, что отношение к «журавлю в небе» – y другое, чем к «синице в руках» – x.
Решением дифференциального уравнения (2.2), если (2.1) справедливо для любого s, будет произвольная дифференцируемая функция F от m аргументов zs (s=1,2,…, m), где вместо аргументов стоят разности fs(xs)-ys(ys), т. е.
f (x, y)=F[y1(y1)-f1(x1), y2(y2)-f2(xs),¼, ym(ym)-fm(xm)]. (2.3)
Кроме того, из (2.3) следует выполнение гипотезы 1 о совпадении. Итак, справедливо следующее утверждение.
Теорема 1. Для выполнения гипотез 1 и 2 (т. е. соотношений (2.1) и (2.2) независимость всех функций из них от человека) необходимо и достаточно, чтобы функция привлекательности имела вид (2.3)
Замечание. Легко ослабить требование гипотезы 1, полагая, она справедлива лишь для людей каждой группы i. Для этого нужно учесть зависимость всех произвольных функций F, f и y от группы, добавив к ним еще индекс i. Кроме того, уже упоминалось монотонно возрастающее преобразование функции привлекательности, переводящее предпочтения в интенсивности перехода, которое может зависеть от группы, содержащей человека x. Это далее используемое преобразование также эквивалентно добавлению индекса i, который отражает влияние группы, но лишь на функцию F.
Результат теоремы говорит лишь о том, что гипотезы 1 и 2 эквивалентны соотношению (2.3). Если же функцию привлекательности невозможно привести к такому виду, то, значит, одна из гипотез несправедлива, но остается не ясным, что нужно править. Слабым утешением служит и то, что все используемые на практике функции легко приводятся к виду (2.3) подбором преобразований факторов f и y функции F.
Таким образом, выполнение требований такого взаимодействия факторов, которое выражается гипотезой 2 о самовозмещении, позволяет еще больше уточнить функцию предпочтения (привлекательности). Но это уточнение означает только, что всегда можно оставить той же самой привлекательность новой группы, возникшей из-за изменения в ней какого-либо фактора, изменением того же самого фактора в старой. Однако остается открытым вопрос о выравнивании привлекательности из-за изменения одного фактора, например, дохода путем изменения других факторов, например, экологических и жилищных условий. В данном случае все зависит от вида произвольной функции F(z1, z2,…., zm), определяющей привлекательность (предпочтение).
Если же заведомо ясно, что все факторы x (и, соответственно, y) можно разделить на несколько совокупностей так, что эффективность действия на предпочтения отдельного человека факторов из одной не подвержены влиянию факторов из другой, то возникает задача: может ли такое свойство независимости эффективности факторов из одной совокупности от значений из другой (или короче независимости по эффективности) дать возможность уточнить функцию предпочтения. Не уменьшая общности, можно начать с двух совокупностей x=(x1, x2) (y=(y1, y2)). Затем, разбивая при возможности одну из них на две части, получим три совокупности и так далее.
Примером возможности разбиения факторов на две совокупности могут служить такие: первая – экологические показатели, вторая – показатели криминальной обстановки. Действительно, разве может повлиять на эффективность действия чистоты (или загрязненности) воды на предпочтения отдельного человека, величина другого фактора – количества хищений автомобилей. И, наоборот, эффективность действия такого параметра, как количество автомобильных краж, вряд ли измениться из-за увеличения или уменьшения загрязненности воды. Другими словами, чистота воды и количество автомобильных краж не изменяют силу влияния (эффективность) друг друга на привлекательность, хотя и оказывают влияние на предпочтения отдельного человека.
Определение. Совокупности факторов x1(y1) и x2 (y2), образующих полный набор x=(x1, x2) [y=(y1, y2)], независимы по эффективности, если величина изменения привлекательности при изменении факторов одной совокупности не зависят от значений факторов другой.
Математически независимость по эффективности означает, что 
– величина изменения привлекательности при изменении (эффективности) факторов из одной совокупности Gi(i=1,2,), где G1ÈG2={1,2,…, m} и G1ÇG2=Æ, не изменяется при изменении факторов из другой – Gj (i¹j); т. е. ei(x, y)=ei(xi, yi) или
" i, j=1,2. (2.4)
Теорема 2. Разбиение факторов x и y, на две совокупности (x1, x2) [x=(x1, x2)] и (y1, y2) [y=(y1, y2)] независимых по эффективности, существует тогда и только
тогда, когда функция привлекательности
f (x, y)=F1 (x1, y1)+F2 (x2, y2). (2.5)
Следствие 1. Все факторы x (y) независимы по эффективности тогда и только тогда, когда
f (x, y)=
. (2.6)
Достаточность условий (2.5) и (2.6) теоремы 2 и следствия 1 для выполнения (2.4) проверяется простым дифференцированием, а необходимость (2.4) следует из решений системы дифференциальных уравнений (2.4) в частных производных, которые имеют общий вид, приведенный в (2.5). Соотношение (2.6) получается из (2.5), в случае, когда вначале отщепляется x1(y1) в качестве множества G1, затем из оставшегося множества G2 выделяется x2 (y2) и т. д. пока в G2 не остается один последний фактор xm (ym).
Следствие 2. Для независимых по эффективности факторов гипотезы 1 о совпадении и 2 о самовозмещении выполнены, когда
f (x, y)=
Fs[fs(ys)-fs(xs)]; (2.7)
и, наоборот, из (2.7) следует, что справедлива гипотеза 1, все факторы x (y) независимы по эффективности и для любого из них выполнена гипотеза 2.
3. Примеры конкретных функций. Теорема 1 и следствия 1 и 2 позволяет ограничить класс функций привлекательности от факторов, которые на практике либо просто равны. либо пропорциональны интенсивностям перехода lij. Разберем несколько примеров, в которых будет рассмотрено попарное изменение факторов, независимо от значений всех остальных, предполагаемых фиксированными.
Пример 1. Пусть привлекательности, пропорциональные интенсивностям перехода, не меняются, если факторы x1 и y1. меняются на одну и ту же величину. Тогда из гипотезы 2, точнее из (2.1) следует, что dx1=dy1.откуда получается.
, а функции y1(z)=f1(z)=z. В этом случае из теоремы 1 следует, что привлекательность будет зависеть от разностей y1- и x1 первых компонент кортежей факторов x и y. Это значит, что lijµF(y1-x1,…), где символ µ обозначает пропорциональность. Примером таких факторов могут служить координаты, определяющие расстояния.
Пример 2. Пусть факторы x2 и y2 в некоторых двух группах, например, отраслях экономики, меняются так, что их относительные приращения dx2/x2 и dy2/y2 одинаковы, т. е. dx2/x2=dy2/y2, и при этом не меняется привлекательность отрасли, предлагающей условия y для человека, находящегося на уровне x. Тогда привлекательности переходов между ними lij зависят лишь от отношения факторов y2/x2. Это следует из того, что из гипотезы 2 получаем y‘2(z)=
. Тогда функции y2(z)=f2(z)=lnz и общий интеграл дифференциального уравнения (2.2) равен lny2-lnx2=ln(y2/x2) =const. Другими словами, из постоянства предпочтений, следовательно, и движения (т. е. постоянства интенсивностей перехода, когда остальные параметры не меняются) при пропорциональном к уже достигнутым уравнениям приращениям факторов следует, что lijµF(…, y2-/x2,…). Заработки людей в отраслях, на предприятиях или регионах служат примером таких благ-факторов подвижности.
Пример 3. Если неизменны предпочтения, определяющие интенсивности перехода, при отношении приростов факторов x3 и y3, обратно пропорциональных к отношению уровней, ими уже достигнутых, т. е. dx3/dy3=1/(x3/y3) или x3dx3=y3dy3. Тогда из условия (2.1) гипотезы 2 следует, что y‘3=
, а y3(z)=f3(z)=2z2. Из результата теоремы 1 теперь имеем lijµF(…,
,…). Это значит, что движение зависит от разности квадратов достигнутых уровней факторов. Возможно, именно такова зависимость отношения честолюбивого человека к престижу должности.
Пример 4. Пусть m=3 и функции Fl (l=1,2,3), фигурирующие следствии 2, линейны, т. е. Fl(z)=al+blz. Если для теоремы 1 F(z)=a+bTz, тогда результирующие функции F от трех аргументов и для следствия 2 и для теоремы 1 совпадают и равны
F(z1, z2, z3)=a+b1z1+b2z2+b3z3.
где для следствия 2 a=a1+a2+a3. а) Допустим, что все факторы удовлетворяют примеру 1. Тогда, если факторами x человек обладает в группе i, а факторы y ему предложены в группе j, то интенсивность его перехода на новое место будет пропорциональна
f (x, y)=a+b1(y1-x1)+b2(y2-x2)+ b3(y3-x3).
б) Если же первый фактор удовлетворяет примеру 1, второй – примеру 2, а третий – примеру 3, то интенсивность переходов одинаково относящихся в силу гипотезы 1 к благам-факторам людей их групп i в группу j будет
lij µf (x, y)=a+b1(y1-x1)+b2ln(y2/x2)+b3(y
-x).
Пример 5. Пусть m=3 и все три фактора удовлетворяют примеру 2, а функция фигурирующая в теореме 1 такова
F(z1, z2, z3)=exp (a+b1z1+b2z2+b3z3).
Тем самым предполагается, что нет независимости по эффективности (см. задачу 2). Тогда интенсивности lij переходов пропорциональны таким функциям от факторов:
f (x, y)=exp [a+b1 ln(y1/x1)+b2 ln(y2/x2)+b3(ln(y3/x3)]=
=A
,
где A=ea. Очевидно, что в этом примере изменения интенсивностей переходов lij и предпочтений при изменении какого-либо одного фактора xl или yl (l=1,2,3) зависит от значений всех остальных факторов, хотя соотношение (2.1) выполнено, а, следовательно, справедливость гипотезы 2 не нарушена.
Во всех примерах гипотеза 1 выполнена, так как все коэффициенты a, A, и bi не зависят от группы, к которой отнесен человек, обладающий набором благ x. Более того, обратим внимание на то, что в примерах нигде не учитывалось различие в коэффициентах пропорциональности f и y приращений факторов-благ. Таким образом, набор функций от факторов, удовлетворяющих условиям гипотез 1 и 2 весьма широк.
Задачи.
1. Пусть I(y1, y2) – индикатор возрастного интервала (y1, y2), где начало и конец – возраст человека (полное число лет), т. е. функция от возраста z, равная 1 при y1,<z<y2. и 0 в остальных случаях. Пусть C означает, что «нужен поп», B – «нужна попадья, A – «нужна попова дочка». Функция F(z)=A·I (18,30)+B·I (0,7)+C·I (60,100). Ответьте на вопросы из поговорки: «кому нужен поп? кому попадья? кому попова дочка?», выраженные последним соотношением.
Похожие работы
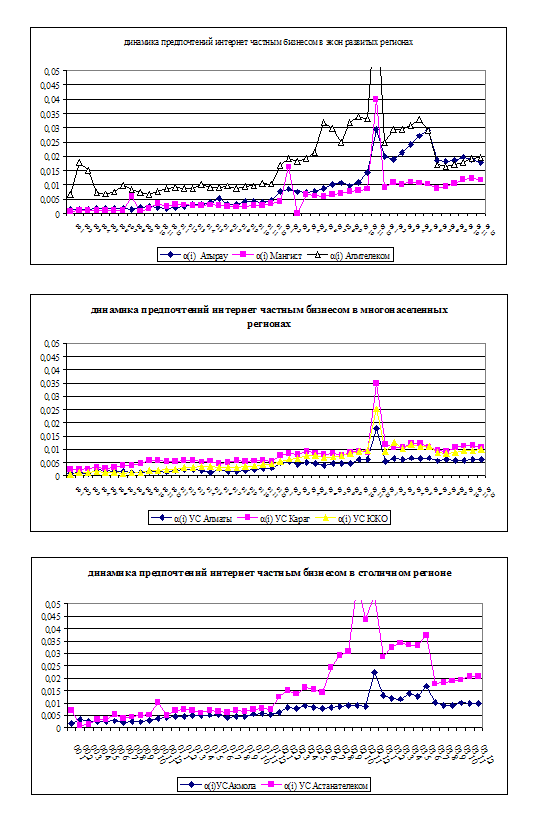
... столичную группу образуют г. Астана, Акмолинская область. 3-ую группу образуют многонаселенные области – ЮКО, Карагандинская, Алматинская области. 9. Первый вариант оценок субъективных предпочтений интернет-услуг частным бизнесом Рассмотрим систему показателей, которая позволяет провести косвенную оценку реакции потребителя интернет-услуг, выражающую в увеличении объема потребляемых услуг, а ...
... , если вместо факторов подвижности подставит их логарифмы. 7. Предельная эффективность факторов Интенсивности переходов f (x, y) (вероятности при дискретном времени) обычно связаны (пропорциональны) функции предпочтения. Поэтому при всех фиксированных условиях (наборах факторов x и y) и интенсивности переходов и предпочтения постоянны. Но возникает вопрос, что будет происходить с этими ...
... 2002г. 2003г. 2004г. 2005г. За 9 мес. 2006г. всего совокупных расходов, грн 541,3 607,0 658,3 736,8 903,5 1229,4 1428,3 Процентов потребительские совокупные расходы 93,3 93,7 92,8 93,3 92,6 91,1 90,5 продовольственные товары (включая питание вне дома, алкогольные напитки и табачные изделия) 67,9 65,4 62,8 62,7 61,7 61,0 58,1 ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
0 комментариев