К.П.Д. магнетрона

1.3 К.П.Д. магнетрона

Трудности, связанные с прямым вычислением отдаваемой электронами мощности, настолько велики, что в настоящее время не существует строгого расчета электронного к. п. д. магнетрона типа бегущей волны. В подобных случаях можно вычислить мощность, рассеиваемую электронами после взаимодействия с полем, и затем использовать закон сохранения энергии

Рассмотрим кинетическую энергию, которую имеет электрон в момент удара об анод после того, как значительная часть потенциальной энергии электрона отдана высокочастотному полю в пространстве взаимодействия.

При обсуждении процессов сортировки электронов было показано, что циклоидальная траектория благоприятного электрона при малой амплитуде высокочастотных колебаний наклоняется в сторону анода, но остается в основном такой же, как в статическом режиме. Радиус катящегося круга в плоском магнетроне равен

, (1.5)

где  - расстояние между катодом и анодом.

Скорость, которую имеет электрон при ударе об анод, зависит от момента удара. Будем исходить из наихудшего с точки зрения величины к. п. д. случая, когда удар происходит в верхней точке циклоидальной траектории. Полюсом вращения является точка касания круга к плоскости, по которой происходит качение этого круга. Радиус вращения электрона равен здесь . Зная угловую скорость вращения круга  нетрудно получить максимальную скорость электрона:

. (1.6)

К такому же результату можно придти, исходя из известной скорости центра круга, равной .

Максимальная кинетическая энергия, рассеиваемая электроном на аноде, равна

 (1.7)

Тот же электрон, находясь на катоде до начала движения в пространстве взаимодействия, обладал по отношению к аноду потенциальной энергией, равной W_n = eU_a, при нулевой кинетической энергии. Следовательно, энергия, отданная высокочастотному полю, по закону сохранения энергии равна W_n —.

К. п. д. рассматриваемого одиночного электрона, таким образом, имеет величину

 (1.8)

Полученное уравнение можно преобразовать, выразив величину  через критические параметры и .

 (1.9)

Уравнение (1.9) показывает связь электронного к.п.д. магнетрона с постоянным анодным напряжением и индукцией магнитного поля. При В = В_кр электронный к.п.д. равен нулю, что вполне согласуется с делавшимися предположениями. Чем больше режим магнетрона отличается от критического, тем выше должен быть электронный к.п.д. Особенно интересно, что никакого теоретического предела повышения величины _эл для магнетрона по рассматриваемым уравнениям не существует.

Зависимость электронного к.п.д. магнетрона от величины магнитного поля В можно сделать особенно наглядной, если учесть условие синхронизма при работе на любом фиксированном виде колебаний. Воспользуемся упрощенным условием самовозбуждения магнетрона:

 (1.10)

Вводя это соотношение в (1.8) и полагая для цилиндрической системы  имеем при

 (1.11)

где - отношение радиуса катода к радиусу анода, равное .

Подставим в (1.11) величины е и m, а также введем резонансную длину волны - го вида колебаний .

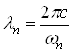Выражая индукцию магнитного поля в тесла и длину волны в сантиметрах, получаем:

 (1.12)

Для оценки получаемого к.п.д. рассмотрим в качестве примера 8-резонаторный магнетрон 10-см диапазона, работающий на -виде колебаний при магнитной индукции 0,18 тл (1800 гс). Величину  примем равной 1/3; такая или близкая к ней величина  типична для магнетронов при N = 8. Вычисления по (1.12) дают: 70%.

Расчетные значения электронного к.п.д. по (1.11) и (1.12) обычно несколько превышают получаемую на практике величину . Отчасти это и понятно, так как в рассмотренном расчете не были учтены потери энергии за счет неблагоприятных электронов, бомбардирующих катод, а также непроизводительные потери электронов на боковые крышки магнетрона и некоторые другие факторы. Величина электронного к.п.д. существующих магнетронов сантиметрового диапазона составляет 50—70%, а в некоторых случаях и более. Столь высокая эффективность магнетронов делает их ценнейшим мощным автогенератором диапазона СВЧ. Для данного магнетрона при неизменной длине волны уравнение (1.11) можно переписать в виде

 (1.13)

Полученное уравнение соответствует случаю, когда к.п.д. отсчитывается при движении вдоль одной из прямых самовозбуждения на плоскости (U_a, В) (см. рис. 1.3, а). Соответствующее графическое изображение зависимости _эл = f(B) для 8-резонаторного магнетрона показано на рисунке1.4, а. Кривые электронного к.п.д. имеют вид отрезков гипербол. Чем ниже номер вида п, тем меньше электронный к.п.д. при одной и той же величине магнитной индукции В. Иначе говоря, для достижения одного и того же электронного к.п.д. наименьшее магнитное поле требуется при -виде колебаний.

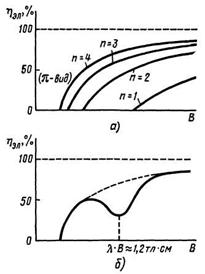
Рисунок 1.4 - Зависимость электронного к.п.д магнетрона от индукции магнитного поля при const

Рост электронного к. п. д. магнетрона при увеличении магнитной индукции В и, напомним, при соответствующем повышении постоянного анодного напряжения _а легко понять с физической точки зрения, так как при этом происходит неограниченное уменьшение радиуса катящегося круга и уменьшение энергии, рассеиваемой электронами на аноде. Такие же тенденции характерны для работы других приборов магнетронного типа. В этом отношении проявляются очевидные отличия и преимущества приборов М-типа в сравнении с приборами О-типа. В приборах М-типа электроны отдают СВЧ полю не кинетическую, а потенциальную энергию, полученную от источника постоянного напряжения. Средняя скорость переносного движения электронов не изменяется, благодаря чему не нарушаются условия синхронизма с полем бегущей волны.

Опыт в основном подтверждает ход зависимости _эл = f(B) при , представленной на рисунке 1.4, а. Однако в случае разнорезонаторных магнетронов в некотором интервале значений магнитной индукции наблюдается "провал" электронного к. п. д., как показано качественно на рисунке 1.4, б. Исследования показали, что в центре "провала" произведение магнитной индукции, выраженной в тесла, на длину волны в сантиметрах имеет для всех магнетронов одинаковую величину, равную приблизительно 1,2 тл.см.

"Провал" электронного к. п. д. в разнорезонаторных магнетронах можно качественно объяснить с точки зрения циклотронного резонанса, возникающего при условии . В пространстве взаимодействия разнорезонаторного магнетрона, кроме поля -вида, имеется составляющая поля п = 0. При приблизительном совпадении частоты генерируемых колебаний и циклотронной частоты характер движения электронов может измениться. Большую роль играет тот факт, что поле нулевой составляющей значительно медленнее убывает при удалении от анода, чем поле -вида .

Форма спиц и их взаимодействие с полем -вида ухудшаются.

Обычно разнорезонаторные магнетроны эксплуатируются при более низком магнитном поле, чем поле, соответствующее центру "провала". Перейти в область больших индукций за "провалом" практически не удается из-за трудностей получения очень сильных магнитных полей.

Некоторое влияние на величину электронного к. п. д. магнетрона оказывает разделение видов колебаний. По-видимому, условия формирования спиц ухудшаются при наличии "загрязняющих" полей в пространстве взаимодействия. Электронный к. п. д. магнетрона может снизиться также за счет влияния поля связок около концов анодного блока. Это поле, не имеющее азимутальных вариаций, оказывает примерно такое же воздействие на пространственный заряд в магнетроне, какое имеет поле нулевой составляющей в магнетронах разнорезонаторной конструкции. Для устранения подобных эффектов связки обычно экранируются путем расположения их в кольцевых канавках, выточенных на торцах анодного блока.

Диаметр катода также влияет на величину электронного к. п. д. Для повышения величины желательно уменьшать отношение . Однако при малом - не могут полностью удовлетворяться условия синхронизма между электронами и полем, так как напряженность постоянного электрического поля имеет наибольшую величину у катода и уменьшается по направлению к аноду. Чтобы повысить электронный к. п. д. магнетрона, обычно рекомендуется выбирать наименьшую возможную величину, при которой получается достаточная устойчивость видов колебаний.

Для оценки оптимального отношения с предложены различные эмпирические соотношения, например:

  (1.14)

где N — число резонаторов. Отметим, однако, что зависимость эл = f() не очень критична и допускает заметные отклонения от величины, рассчитанной по уравнениям (1.14).

В заключение напомним, что полный к. п. д. магнетрона определяется с учетом к. п. д. резонаторной системы:

 (1.15)

Как известно, величина  в общем случае связана с собственной, нагруженной и внешней добротностями колебательной системы соотношением

 (1.16)

Величина внешней добротности выбирается с учетом допустимого затягивания частоты магнетрона и обычно не бывает ниже 100—200. Собственную добротность  желательно иметь как можно выше. Типичная величина в сантиметровом диапазоне имеет порядок 1000. Таким образом, по (1.16) к. п. д. резонаторной системы может составлять от 90—95% до 60—65% на наиболее коротких волнах. Типичные значения полного к. п. д. магнетронов составляют от 60—70% на дециметровых волнах до 20—30% на волнах длиной порядка 1 см.

Похожие работы

Передатчик импульсный СВЧ диапазона

Скачать

14694

4

9

... функционально-узлового метода конструирования, повышающего надёжность аппаратуры и её качественные показатели; широкое применение цифровых устройств. В данной курсовой работе предлагается спроектировать импульсный передатчик для наземной радиолокационной станции. Радиолокация решает задачи обнаружения, определения координат и параметров движения различных объектов с помощью отражения или ...

Выбор и обоснование тактико-технических характеристик РЛС. Разработка структурной схемы

Скачать

45419

3

0

... обзора земли с целью обеспечения возможности автономной навигации по характерным наземным радиолокационным ориентирам.   3. Обоснование, выбор и расчет тактико-технических характеристик радиолокационной станции 3.1. Обоснование, выбор и расчет тактических характеристик РЛС 3.1.1. Максимальная дальность действия RmaxМаксимальная дальность действия задается тактическими требованиями и зависит ...

Научные проблемы создания высокоточного оружия флота

Скачать

75759

0

0

... техническому совершенству, боевым и эксплуатационным качествам не уступали лучшим зарубежным образцам, а нередко и превосходили их. Большинство из созданных в эти годы образцов в большей или меньшей степени представляли собой высокоточное оружие. В них использовались высокоточные инерциальные системы, системы коррекции и телеуправления движением на траектории и системы самонаведения на конечном ...

Радиолокационная Головка Самонаведения

Скачать

37104

0

12

... систем в РЛГС четыре: 3.2.1 Радиолокационная часть РЛГС Радиолокационная часть РЛГС состоит из: ·     передатчика. ·     приемника. ·     высоковольтного выпрямителя. ·     высокочастотной части антенны. Радиолокационная часть РЛГС предназначена: ·     для генерирования высокочастотной электромагнитной энергии заданной частоты (f±2,5%) и мощности 60 Вт, которая в виде коротких ...