Навигация
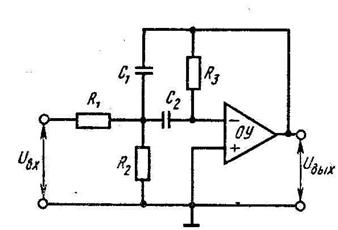
Фильтры верхних частот на одном усилителе с положительным коэффициентом усиления
1.1 Фильтры верхних частот на одном усилителе с положительным коэффициентом усиления
Обобщенная передаточная функция по напряжению ФВЧ второго порядка имеет вид
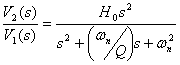 (1.1)
(1.1)
В этом выражении Н0 — коэффициент передачи на бесконечно большой частоте, ωn – собственная частота, Q –добротность.
Преобразуя (1.1) получаем:
![]() (1.2)
(1.2)
Сравнивая (1.1) и (1.2) и анализируя результат можно получить первый вариант расчетных формул. Выбирая R2=R4=R и С1=Сз=С, получаем:
![]() ; 1/Q=3-K; H0=K, (1.3а), (1.3б), (1.3в)
; 1/Q=3-K; H0=K, (1.3а), (1.3б), (1.3в)
Реализацию ФВЧ второго порядка можно получить подстановкой К=1. Полагая m=С3/С1, и n=R4/R2 и подставляя С1=С и R2=R, получаем вместо (1.2)
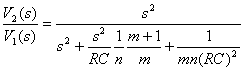 (1.4)
(1.4)
Сравнивая полученное с (1.1), находим еще один вариант расчетных формул (вариант 2):
![]()
![]() (1.5)
(1.5)
Отсюда видно, что для любого заданного значения п минимум 1/Q достигается при m=1. Так как обычно желательно иметь минимум 1/Q для любого заданного п, то примем m=1. В этом случае (1.5) упрощается и принимает вид
![]()
![]() (1.6)
(1.6)
В другом используемом на практике наборе номиналов элементов RС-фильтра верхних частот на одном усилителе с положительным коэффициентом усиления, емкости обоих конденсаторов имеют равные номиналы, а коэффициент усиления ИНУН равен двум. Тогда нормированные значения С1=С3=С и K=2. Используя выражение (1.2), в этом случае находим
![]()
![]() (1.7)
(1.7)
Преимущество структурs Саллена и Ки на усилителе с положительным коэффициентом усиления заключается в том, что она характеризуется в общем случае простыми расчетными соотношениями; проектировщик имеет возможность легко управлять значениями номиналов элементов и их разбросом; кроме того, допустимо использовать небольшие значения коэффициента усиления ИНУН, которые удобны тем, что их легко стабилизировать. Есть также и некоторые недостатки; основной из них состоит в том, что она характеризуется высокими значениями чувствительности, если с их помощью пытаются реализовать схемы с высоким Q.
1.2 Фильтры, реализующие комплексно-сопряженные нули
Рассмотрим реализации активных фильтров для обобщенной передаточной функции второго порядка. Их обычно относят к биквадратным функциям фильтрации. Общий вид биквадратных передаточных функций по напряжению второго порядка такой
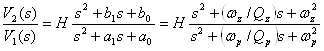 (1.8)
(1.8)
где Н — постоянная, ωz и ωp— нули и полюсы, соответствующие собственным частотам, а Qz и Qp—добротности комплексных нулей и полюсов. Предполагается, что нули могут быть вещественными или комплексными и что они могут быть расположены в любом месте на плоскости комплексной частоты, включая и правую полуплоскость.
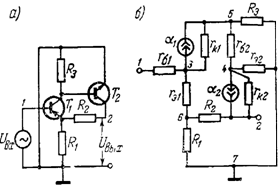
Первый тип биквадратного фильтра реализуется на основе схемы с одним усилителем и конечным коэффициентом усиления.
Предполагая, что нули расположены ближе к началу координат, чем полюсы, получаем следующие расчетные соотношения:
![]() ;
; ![]() ; (1.9а), (1.9б)
; (1.9а), (1.9б)
![]() ; Н=К (1.9в), (1.9г)
; Н=К (1.9в), (1.9г)
Множитель т можно выбрать произвольно.
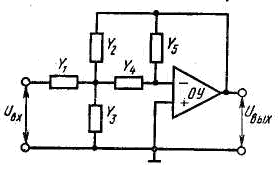
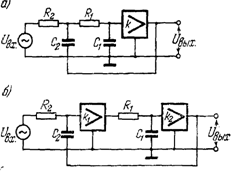
Второй тип биквадратного фильтра реализуется одним усилителем с бесконечным коэффициентом усиления. Здесь используется операционный усилитель с дифференциальным входом. Передаточную функцию такого фильтра легко найти
![]() (1.10)
(1.10)
Если Y1+Ya+Y4=Y2+Yb+Y3 или Ya=Y2+Y3 или Yb=Y1+Y4, то (1.10) примет вид
![]() (1.11)
(1.11)
В третьем типе реализации биквадратного фильтра используются два операционных усилителя. Анализ этой схемы дает
![]() ,что совпадает с (1.11).
,что совпадает с (1.11).
Рассмотрим еще одну реализацию биквадратного фильтра. В ней используются двойные Т-образные цепи в качестве пассивных компонентов. Передаточная функция фильтра по напряжению
![]() (1.12), где
(1.12), где
b+2=g+e; f+2=d; T=RC. (1.13)
Из (1.8) и (1.13) получаем
![]() ;
; ![]() ;
;
![]() ;
;![]() ;
; ![]() . (1.14)
. (1.14)
Если Н0, ωp, ωz, Qp и Qz подлежат определению, то приведенные уравнения можно разрешить относительно параметров а, Ь, е, f, g, R и С.
Для ФВЧ g=b=0, e=2, 2+f=d.
Похожие работы
... усилителя от приведенного ко входу ЭДС смещения ОУ2. Приведенные результаты показывают, что дрейф нуля и коэффициент ослабления синфазного напряжения определяются только мультидифференциальным операционным усилителем. Соотношения (90), (94) показывают, что основным преимуществом классической структуры инструментального усилителя (рис. 12) является независимость коэффициента передачи синфазного ...
... со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью ее реализации. Это называется "проблемой аппроксимации". Во многих случаях ...
... даже иногда вредным. Однако превратить УПТ в усилитель переменного тока можно достаточно просто (например, вводя разделительные емкости). Поэтому большинство массовых операционных усилителе выпускаются как усилители постоянного тока. Условное обозначение ОУ приведено на рисунке 7.1. В обозначении функции (¥ > – усилитель с бесконечно большим коэффициентом усиления) первый символ (¥) ...
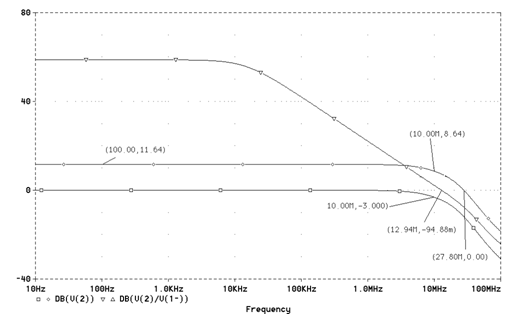
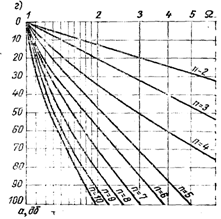
... целесообразно решать аппроксимационную задачу. Определим нормированную частоту ограничения фильтра, как отношение = = 0,6666. Нормированная частота в полосе задерживания обычного фильтра НЧ равна . Эта же частота в случае фильтра НЧ с ограниченной полосой пропускания рассчитывается по формуле Из кривых (рис. 1.) по вычисленной и заданным и а определим ...

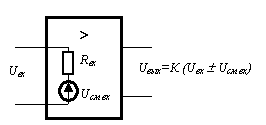

0 комментариев