Навигация
Радиотехническая система передач
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра радиотехнических систем
РЕФЕРАТ
На тему:
«Параметры кодов. Контроль, обнаружение и исправление ошибок»
МИНСК, 2008
1. Параметры кодов
Определение 1. Код – это множество дискретных сигналов, выбранное для передачи сообщений. Коды характеризуются следующими параметрами:
1 Основание кода ![]() – число элементов множества
– число элементов множества ![]() , выбранное для построения кода. Например, если:
, выбранное для построения кода. Например, если:
а) ![]() , то
, то ![]() для троичного кода;
для троичного кода;
б) ![]()
![]() для двоичного кода.
для двоичного кода.
Практически ![]() .
.
Замечание – Эффективность каналов передачи (хранения) информации возрастает с переходом на недвоичные коды.
2 Длина кода ![]() (значность) – число символов кодового слова.
(значность) – число символов кодового слова.
Определение 2. Последовательности элементов (символов) длиной ![]() называются кодовыми словами или кодовыми векторами. Говорят, что слово
называются кодовыми словами или кодовыми векторами. Говорят, что слово
![]() имеет длину
имеет длину ![]() ;
; ![]() ,
, ![]()
Параметр ![]() определяет следующие особенности класса кодов. Коды бывают:
определяет следующие особенности класса кодов. Коды бывают:
а) равномерные (блоковые), ![]() ;
;
б) неравномерные, ![]() ;
;
в) бесконечные, ![]() . К бесконечным относят коды:
. К бесконечным относят коды:
1) свёрточные;
2) цепные;
3) непрерывные.
У равномерных (блоковых) кодов поток данных разделяется на блоки по ![]() информационных символов, и далее они кодируются
информационных символов, и далее они кодируются ![]() –
символьными кодовыми словами.
–
символьными кодовыми словами.
Для непрерывного кода поток данных разбивается на блоки длины ![]() , которые называются кадрами информационных символов. Эти кадры кодируются
, которые называются кадрами информационных символов. Эти кадры кодируются ![]() символами кодового слова (кадрами кодового слова). При этом кодирование каждого кадра информационных символов в отдельные кадры кодового слова производится с учетом предыдущих
символами кодового слова (кадрами кодового слова). При этом кодирование каждого кадра информационных символов в отдельные кадры кодового слова производится с учетом предыдущих ![]() кадров информационных символов.
кадров информационных символов.
k-битовый n-битовый n-битовый k-битовый
 блок блок блок блок
блок блок блок блок
k0 битов/кадр n0 битов/кадр n0 битов/кадр k0 битов/кадр

Непрерывный код
Рисунок 1.1
3 Размерность кода ![]() – число информационных позиций кодового слова.
– число информационных позиций кодового слова.
4 Мощность кода ![]() – число различных кодовых последовательностей (комбинаций), используемых для кодирования.
– число различных кодовых последовательностей (комбинаций), используемых для кодирования.
![]() – максимальное число кодовых комбинаций при заданных
– максимальное число кодовых комбинаций при заданных ![]() и
и ![]() . Например,
. Например, ![]() ;
; ![]() ;
; ![]() .
.
Определение 3. Код, у которого используются все комбинации, называется полным (безизбыточным).
Определение 4. Если число кодовых слов кода ![]() , то код называется
избыточным.
, то код называется
избыточным.
Пример – Пусть ![]() ,
, ![]() ,
, ![]() .
.
Код ![]()
 – избыточный;
– избыточный; ![]() .
.
5 Число проверочных (избыточных) позиций кодового слова ![]() .
.
Пусть ![]() ,
, ![]() ,
, ![]() . Тогда на длине слова из семи символов – три избыточных.
. Тогда на длине слова из семи символов – три избыточных.
6 Скорость передачи кода ![]() . Для приведенного примера
. Для приведенного примера
![]() .
.
7 Кратность ошибки ![]() . Параметр
. Параметр ![]() указывает, что все конфигурации из
указывает, что все конфигурации из ![]()
или менее ошибок в любом кодовом слове могут быть исправлены.
8 Расстояние Хэмминга между двумя векторами (степень удаленности любых кодовых последовательностей друг от друга) ![]() .
.
Определение 5. Если ![]() и
и ![]()
![]() кодовые векторы, то расстояние Хэмминга равно числу позиций, в которых они различаются. Может обозначаться и как –
кодовые векторы, то расстояние Хэмминга равно числу позиций, в которых они различаются. Может обозначаться и как – ![]() . Например,
. Например, ![]() ;
;![]() .
.
Замечание – С позиции теории кодирования ![]() показывает, сколько символов в слове надо исказить, чтобы перевести одно кодовое слово в другое.
показывает, сколько символов в слове надо исказить, чтобы перевести одно кодовое слово в другое.
9 Кодовое расстояние (минимальное расстояние кода) ![]() .
.
Определение 6. Наименьшее значение расстояния Хэмминга для всех пар кодовых последовательностей кода называют кодовым расстоянием. ![]() , где
, где ![]() ;
; ![]() ;
; ![]() .
.
Определение 7. Код значности ![]() , размерности
, размерности ![]() и расстояния
и расстояния ![]() называется
называется ![]() - кодом.
- кодом.
Пример – Можно построить следующий код:
![]()
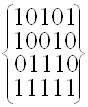 ;
; ![]() ;
; ![]() ;
; ![]() .
.
Данный код можно использовать для кодирования 2–битовых двоичных чисел,
используя следующее (произвольное) соответствие:

Найдем кодовое расстояние этого кода:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Следовательно, для этого кода ![]() .
.
Замечание – ![]() характеризует корректирующую способность кода
характеризует корректирующую способность кода ![]() .
.
10 Вес Хэмминга вектора ![]() равен числу ненулевых позиций
равен числу ненулевых позиций ![]() , обозначается
, обозначается ![]() . Например,
. Например, ![]() .
.
Используя определение веса Хэмминга, получим очевидное выражение ![]() (1.1)
(1.1)
Пример – ![]() ;
;
|
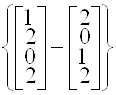
Из выражения (1.1) следует, что минимальное расстояние Хэмминга равно ![]() , где
, где ![]() ;
; ![]() ;
; ![]() .
.
Теорема 1. Минимальное расстояние линейного кода равно минимальному весу ненулевых кодовых слов.
Т.к. ![]() , то возникает вопрос о величине
, то возникает вопрос о величине ![]() , такой, чтобы код обеспечивал контроль ошибок, т.е. обнаружение и исправление ошибок.
, такой, чтобы код обеспечивал контроль ошибок, т.е. обнаружение и исправление ошибок.
2 Контроль ошибок
Кодовое слово можно представить в виде вектора с координатами в ![]() – мерном векторном пространстве. Например, для
– мерном векторном пространстве. Например, для ![]() вектор
вектор
![]() находится в трёхмерном евклидовом пространстве, рисунок 1.2. Разрешенными для передачи выбраны вектора
находится в трёхмерном евклидовом пространстве, рисунок 1.2. Разрешенными для передачи выбраны вектора ![]() и
и ![]() .
.
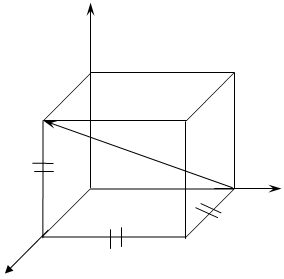 X0
X0
1 0 0 1 1 0
1 0 1 1 1 1
0 0 0 0 1 0 X1
0 0 1 0 1 1
X2
Рисунок 1.2Рисунок дает наглядную алгебраическую интерпретацию понятия “мощность кода”:
а) кодовые слова полного кода определяют ![]() – мерное пространство, состоящее из
– мерное пространство, состоящее из ![]() последовательностей (
последовательностей (![]() – трехмерное пространство, состоящее при
– трехмерное пространство, состоящее при ![]() из 8
последовательностей полного кода);
из 8
последовательностей полного кода);
б) кодовые слова избыточного кода определяют подпространство (подмножество) ![]() – мерного пространства, состоящее из
– мерного пространства, состоящее из ![]() последовательностей.
последовательностей.
Под воздействием помех происходит искажение отдельных разрядов слова. В результате разрешённые для передачи кодовые векторы переходят в другие векторы (с иными координатами) – запрещённые. Факт перехода разрешённого слова в запрещённое для передачи слово можно использовать для контроля за ошибками.
Возможна ситуация, когда разрешённый вектор переходит в другой разрешённый кодовый вектор: ![]()
![]()
![]() . В этом случае ошибки не обнаруживаются, и контроль становится неэффективным.
. В этом случае ошибки не обнаруживаются, и контроль становится неэффективным.
Из рассмотренной модели можно сделать следующий важный вывод: для
того чтобы передаваемые векторы можно было бы отличать друг от друга при наличии помех, необходимо располагать эти векторы в ![]() – мерном пространстве
– мерном пространстве
как можно дальше друг от друга. Из этой же ![]() – мерной модели следует геометрическая интерпретация расстояния Хэмминга:
– мерной модели следует геометрическая интерпретация расстояния Хэмминга: ![]() – это число рёбер, которыенужно пройти, чтобы перевести один вектор в другой, т.е. попасть из вершины одного вектора в вершину другого.
– это число рёбер, которыенужно пройти, чтобы перевести один вектор в другой, т.е. попасть из вершины одного вектора в вершину другого.
Похожие работы
... канала управления, способ его организации, протокол взаимодействия. СОДЕРЖАНИЕ СОДЕРЖАНИЕ. 4 ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ СОКРАЩЕНИЙ. 5 Расчет параметров радиотехнической системы.. 6 1. Расчет параметров преобразования сообщения в цифровую форму. 6 2. Расчет параметров канала связи «объект - ЦП». 8 3. Расчет параметров радиолинии «ЦП - объект». 12 4. Выбор характеристик системы определения ...
... сигналов. 1. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ. 1.1. Вводные замечания. В предисловии дано обоснование направленности содержания курсовой работы с учетом места курса "Радиотехнические цепи и сигналы" в подготовке радиоинженеров. Задание учитывает устойчивые тенденции перехода от аналоговых систем к цифровым системам передачи и обработки непрерывных сообщений на основе дискретизации, ...
... , числовых данных, компьютерных файлов и т.п., то есть там, где недопустимы даже малейшие отличия исходных и восстановленных данных. Во многих случаях нет необходимости в абсолютно точной передаче информации от источника к ее потребителю, тем более что в канале связи всегда присутствуют помехи и абсолютно точная передача в принципе невозможна. В таких случаях может быть использовано разрушающее ...
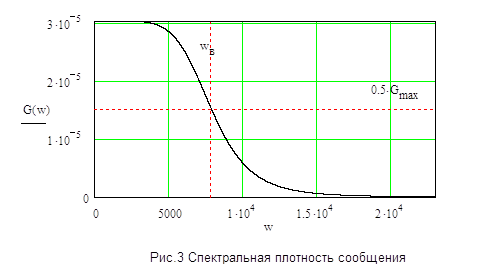
... математического ожидания В этой части необходимо выбрать и рассчитать параметры преобразования аналогового сообщения в цифровой первичный сигнал (двоичный код) для передачи в информационном канале системы измерения и сбора информации. Сообщение представлено в виде реализации случайного стационарного процесса, заданного плотностью распределения своих мгновенных значений W(x) и спектральной ...
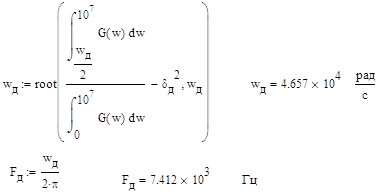
0 комментариев