Требования, предъявляемые к электрическим параметрам антенн ЗССС
Требования к параметрам антенн для ЗССС системы связи "Интерспутник"
Российские требования на параметры антенн для ЗС
Расчет эксцентриситета малого зеркала гиперболы, фокусных расстояний зеркал и диаметра облучателя
Расчет электрических характеристик, допуск на изготовление
Вначале находится поле в раскрыве антенны (внутренняя задача) (см. параграф 2.7)
Техника безопасности и охрана труда
Навигация
Расчет эксцентриситета малого зеркала гиперболы, фокусных расстояний зеркал и диаметра облучателя
Расчет антенны для земной станции спутниковой системы
36838
знаков
6
таблиц
18
изображений
2.3 Расчет эксцентриситета малого зеркала гиперболы, фокусных расстояний зеркал и диаметра облучателя
;
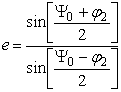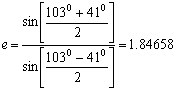
Помимо аналитического вычисления эксцентриситета малого зеркала гиперболы, приведем графическое. На рисунке 2.1 представлены графики, показывающие значения изменения эксцентриситета образующей гиперболы в зависимости от углов (Ψ0) и (φ2).
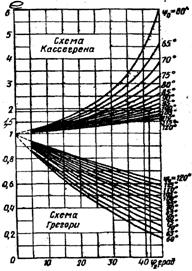
Рисунок 2.1 – зависимость эксцентриситета от углов (Ψ0) и (φ2).
Из графика видно, что при углах Ψ0=1030 и φ2=410 значение эксцентриситета близко к полученному при аналитических вычислениях результату: 
.
Для дальнейшего расчета нам необходимо определить фокусное расстояние большого (F) и малого (f) зеркал. Это можно сделать, используя следующее соотношение:
;
Из приведенного выше соотношения видно, что Fэ определится как:
;
Теперь рассчитаем фокусное расстояние малого зеркала, при этом формула для его определения выглядит следующим образом:
;
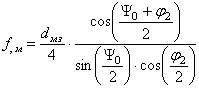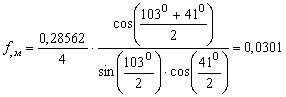
Как известно, разность расстояний от фокусов до произвольной точки на поверхности гиперболоида постоянна, т.е. 
, где 2а – это расстояние между его вершинами. Расстояние между фокусами гиперболоида 
. При этом эксцентриситет образующей гиперболы равен 
. Наглядно расстояние 2а и 2С представлены на рисунке 2.2.
Рисунок 2.2 – графическое представление расстояний 2С и 2а
Теперь мы можем отыскать численные значения расстояний 2С и 2а. Для этого используем выражение:
;
;
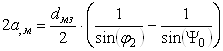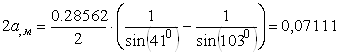
Выполним проверку на условие 
, условие удовлетворено, следовательно, расстояния найдены, верно.
На завершающем этапе расчета данного параграфа нам необходимо определить диаметр облучателя:
;
Таким образом, диаметр облучателя можно определить как:
;
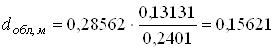
При этом условие 
выполняется.
2.4 Расчет профилей большого и малого зеркал
Данный расчет производится на основе известных выражениях для ρ(ψ) как для большого зеркала параболоида, так и для контррефлектора. Эти выражения выглядят следующим образом,
;
;
для большого и малого зеркал соответственно.
Для упрощения алгоритма вычислений в курсовой работе данный расчет был произведен и запрограммирован с помощью приложения MathCAD professional.
На первом этапе рассчитаем профиль параболы:
Значение угла ψ будет варьировать от (– ψ0)до (ψ0). В результате получим значения для ρ(ψ), которые приведены ниже.
для большого зеркала для малого зеркала
На рисунке 2.3 выполненном в полярных координатах представлены профили обоих зеркал. На рисунках 2.4 и 2.5(а,б) данные профили изображены отдельно, при чем на (рис. 2.5б) профиль параболы представлен в полярных координатах.
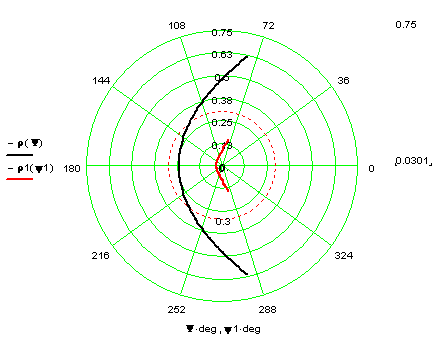
Рисунок 2.3 – профили параболы (черная) и гиперболы (красная)
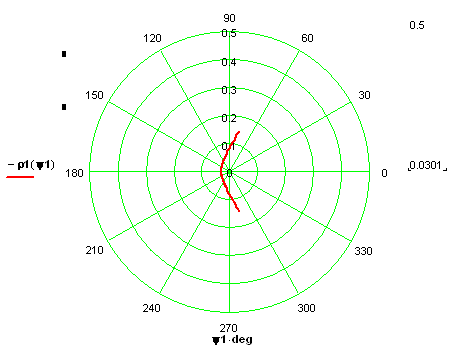
Рисунок 2.4 – контррефлектор
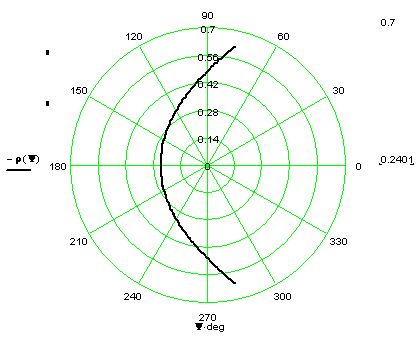
а) профиль большого зеркала
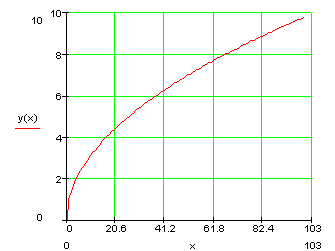
б) профиль большого зеркала в прямоугольных координатах
Рисунок 2.5 – изображение параболоида
Похожие работы
... и прочее). Основное преимущество таких систем связи заключается в возможности значительного расширения зон обслуживания по сравнению с радиорелейными и кабельными линиями связи. Теоретические разработки в области энергетических возможностей линий спутниковой связи позволили сформулировать тактико-технические требования к устройствам спутникового ретранслятора и наземных устройств, исходя из ...
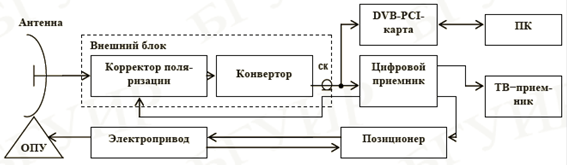
... Прием сигналов осуществляется в г. Гродно с географическими координатами ψ=53,700 с.ш., φз=23,800 в.д. с спутника HotBird 6/7A (130 з.д.) Большинство современных систем индивидуального и коллективного приёма программ спутникового вещания оснащены опорно-поворотным устройством (ОПУ) для оперативного наведения антенны на заданный ИСЗ. Наиболее простым механизмом перестройки антенны ...
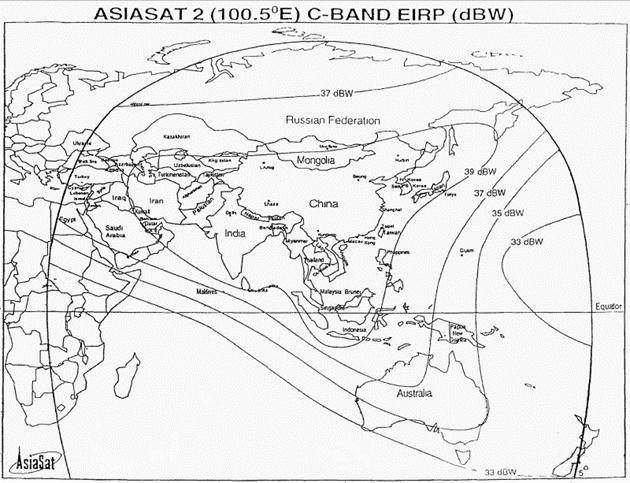
... в зоне с ЭИИМ = 39 дБ; Атырау в зоне с ЭИИМ = 37 дБ. Преобразуем формулу (2.5). (2.6) Вычислим усиление антенны спутника в направлении на Алматы: на Атырау: Произведем расчет дополнительного затухания при распространении радиоволн в атмосфере. Воспользуемся формулой, приведенной в /5/: (2.7) где - дополнительное ...
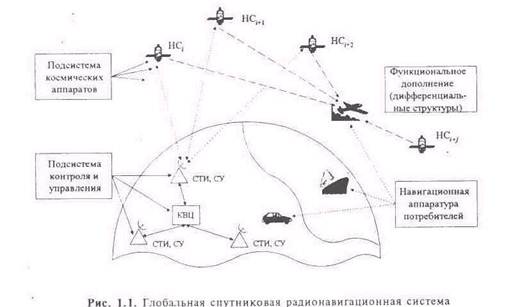
... , используют радиально-скоростные методы. 5. СРНС ГЛОНАСС 5.1. Структура и основные характеристики Отечественная сетевая среднеорбитальная СРНС ГЛОНАСС (ГЛОбальная НАвигационная Спутниковая Система) предназначена для непрерывного и высокоточного определения пространственного (трехмерного) местоположения вектора скорости движения, а также времени космических, авиационных, ...
0 комментариев