Навигация
1. код Баркера;
2. M–последовательность.
Выберем M–последовательность, элемент последовательности, которой рассчитывается по формуле:
![]() (19)
(19)
где ![]() и d – двоичные числа.
и d – двоичные числа.
![]() Составим M-последовательность для информационного элемента. Для этого зададим первые четыре импульса:
Составим M-последовательность для информационного элемента. Для этого зададим первые четыре импульса:
![]()
![]()
Рассчитаем остальные элементы:

Т.о., мы получили М-последовательность для информационного элемента: 011110101100100
Единиц должно быть больше, чем нолей на один разряд (шумоподобнй сигнал).
Информационная последовательность шифруются одними начальными, а синхроимпульс другими начальными условиями.
М-последовательность для синхроимпульса будет запушена в обратном направлении информационная последовательность: 1.
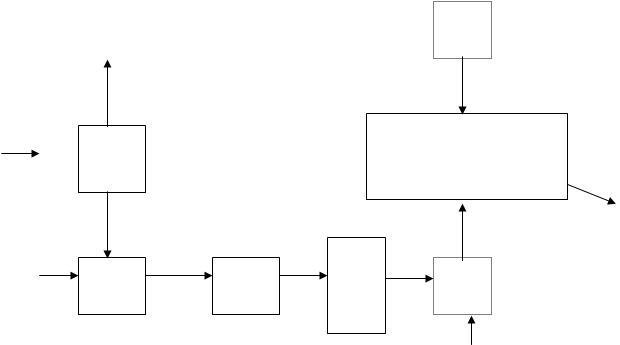
По этим данным строим структурную схему согласованного фильтра для информационной М-последовательности.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|
|

На выходе будем иметь сигнал, амплитуда которого в 15 раз будет больше за счет задержки наших импульсов.
Один сигнал должен быть использован для синхронизации, второй – для передачи информационных символов.
Далее строим функцию корреляции для информационного сигнала, поданного на вход СФинф.
Таблица 1
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||||||||
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||||
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||||||||
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||||
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||||
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | ||||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | ||||||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | |||||||||||||
| -1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | ||||||||||||||
| 1 | 0 | -3 | 0 | -1 | -2 | -1 | 0 | 1 | 0 | -1 | 2 | -1 | -2 | 15 | -2 | -1 | 2 | -1 | 0 | 1 | 0 | -1 | -2 |
Нашу М-последовательность мы либо инвертируем (умножаем на «-1» нашу комбинацию), либо оставляем такой, какая есть. Затем складываем столбцы. Нули заменяются на «-1», а единицы – на «+1». Разность между «+1» и «-1» является результатом, который записывается после черты. По этим результатом строим функцию корреляции.

Рисунок 4 – Функция корреляции – информационный сигнал.
Затем строим функцию корреляции для синхроимпульса, поданного на вход СФинф.
Таблица 2
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | |||||||||||||||
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||||||||||
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| -1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||
| 1 | 0 | -3 | 0 | -1 | -2 | -1 | 0 | 1 | 0 | -1 | 2 | -1 | -2 | 15 | -2 | -1 | 2 | 0 | 0 | 2 | 0 | -1 | -2 | -1 | 0 | -3 | -1 | 1 |
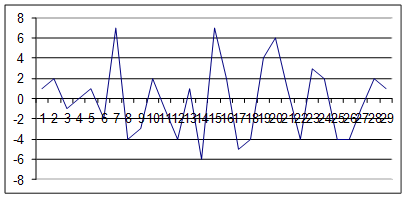
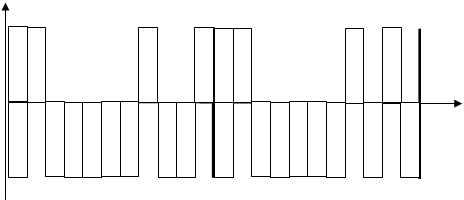
Рисунок 5 – Функция корреляции – сигнал синхронизации.
По полученным ранее данным построим структурную схему согласованного фильтра для синхронизирующей М-последовательности.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|
|
|
|
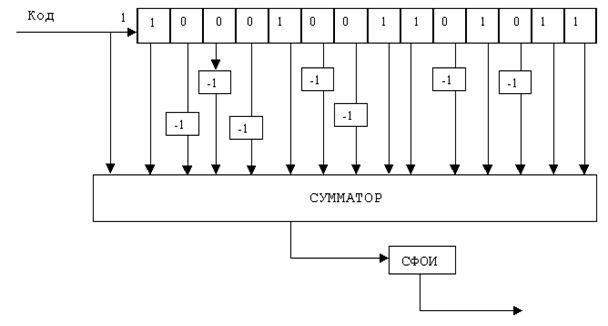
Рисунок 6 – Структурная схема фильтра для синхронизирующей последовательности
Заключение
В результате курсовой работы я закрепила навыки по анализу систем передачи непрерывных сообщений цифровыми методами, расчет характеристик помехоустойчивости и других показателей качества передачи информации по каналу связи с помехами. Мною была разработана структурная схема системы передачи непрерывного сообщения в цифровой форме.
Приведём все основные результаты, полученные в результате произведённых в курсовой работе расчетов, в таблице 3.
Таблица 3
| Величина | Значение |
| 1 Эффективные значения относительных среднеквадратичных ошибок этапов входных преобразований и ошибки, вызванной действием помех | 0,0075 |
| 2 Значение частоты дискретизации Fд | 4500 Гц |
| 3 Значение пик-фактора H | 3,47 |
| 4 Число разрядов двоичного кода Nр | 9 |
| 5 Требуемое значение отношения сигнал/шум для обеспечения пропускной способности канала связи |
|
| 6 Требуемое отношение q2 при оптимальном когерентном приёме | 43 |
| 7 Требуемое отношение q2 при оптимальном некогерентном приёме | 48 |
Методы повышения информационной эффективности :
- разнесенный прием – передача одной и той же информации по параллельным каналам;
- прием в целом - демодулятор строится сразу на все кодовое слово, что позволяет в сравнении с посимвольным приемом повысить верность ;
- обратная связь – система с решающей обратной связью являются примером согласованного подхода к кодированию и модуляции с учетом свойств канала связи;
- применение шумоподобных сигналов – позволяет повысить верность передачи за счет повышения отношения сигнал/шум на входе решающего устройства;
- адаптивная коррекция – осуществление адаптивной коррекции характеристик канала позволяет повысить скорость передачи информации за счет ослабления межсимвольных искажений;
- эффективное кодирование источника – кодирование источника со сжатием данных позволяет сократить избыточность источников сигналов и тем самым повысить эффективность систем передачи информации.
Список литературы
1. Теория электрической связи: Методические указания по изучению курса и выполнению курсовой работы./Д. В. Астрецов, Екатеринбург, УФ СибГУТИ, 2001
2. Теория электрической связи: Учебник для вузов/А.Г. Зюко, Д.Д. Кловский, В.И. Коржик, М.В. Назаров; Под ред. Д.Д. Кловского.
- М: Радио и связь, 1998.
3. Теория электрической связи: Учебное пособие для вузов/ Т.Д. Алексеева, Н.В. Добаткина, Г.К. Кожанова, Н.Т. и др.; Под ред. В.Г. Санникова. - М.: МИС, 1991.
4. Теория электрической связи: Учебное пособие/А.С. Аджемов, М.В. Назаров, Ю.В. Парамонов, В.Г. Санников. - М.: МТУСИ, 1996.
5. Теория электрической связи: Учебник для вузов./Клюев Л.Л.- Минск: Дизайн ПРО, 1998.
Приложение. Структурная схема ИКМ – ЧМ
Тактовые интервалы
Возьмем два числа, например 521 и 522.
Переведем каждое число в двоичную форму:
521 = 1000001001
522 = 1000001010
Похожие работы
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...
... Вид сигнала при модуляции прямоугольными импульсами со скважностью 2: рис. 3 Для отыскания спектра сигнала ДФМ запишем: Спектры сигналов для различных значений: Рис. 4 2.3 Расчет вероятности ошибки на выходе приемника. Вероятность ошибки на выходе приемника определяется формулой где Ф() – функция Крампа q – отношение мощности сигнала к ...
... взаимной нестабильности несущей частоты излучаемого сигнала и частоты настройки приемника и доплеровского сдвига. 2.2 Расчет энергетических характеристик Качество выделения информации приемным устройством цифровой системы передачи информации, связано с вероятностью ошибки приёма разряда сообщения. Связь между допустимым значением вероятности ошибки Рд и пороговым отношением мощности сигнала к ...
... модуляцией, можно сделать вывод, что помехоустойчивость приемника, использующего в качестве информационного параметра фазу, почти приближена к вероятности ошибки приемника Котельникова. 3. Оптимальная фильтрация. Отметим, что оптимальный приемник, является корреляционным, сигнал на его выходе представляет собой функцию корреляции принимаемого и ожидаемого сигналов, благодаря чему ...




0 комментариев