Навигация
Контрольная работа
по дисциплине
«Теория телетрафика»
Законы распределения случайной величины
Таблица1 Исходные данные
Вариант | Емкость АТС | Nнх | Nкв | Cнх | Tнх | Cкв | Tкв | N1 ГИ | Тип блока 1ГИ |
| 9 | 8000 | 3200 | 4800 | 3,4 | 120 | 1,1 | 140 | 1200 | 80*120*400 |
Задание 1
1.Построить огибающую распределения вероятности занятия линий в пучке из v , на каждую из которых поступает интенсивность нагрузки а, при условии, что:
а) N ≈ v;
6) N>>v;
в) N, v → ∞.
2. Для каждого используемого распределения рассчитать среднее число занятых линий и их дисперсию.
Для расчета число линий в пучке определить из следующего выражения:
(целая часть полученного числа), где NN - номер варианта.
Средняя интенсивность нагрузки, поступающей на одну линию:
для NN ≤15:а = 0,15+0,05(15-NN); для 15 < NN ≤ 25:а= 0,05 +0,05(26-NN).
Примечания.
Для огибающей распределения привести таблицу значений Рi, и i
В распределении Пуассона привести шесть - восемь составляющих, включая значения вероятности для i=[Y] (целая часть числа Y); Y = a*v
Решениеа) Распределение Бернулли (биноминальное распределение) при N ≤ v имеет вид:
,
где 
можно рассматривать как вероятность занятия любых i линий в пучке из v;
- числоо сочетаний из 
а – средняя интенсивность поступающей нагрузки на одну линию v – линейного пучка от N источников а =0,15+0,05(15-NN)= 0,15+0,05(15-9)=0,45
v – число линий в пучке 
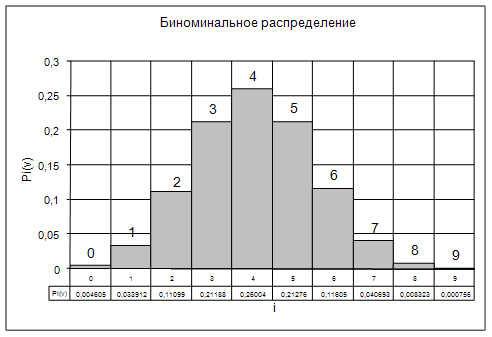
Рисунок1 Биноминальное распределение
Математическое ожидание и дисперсия числа занятых линий, вероятность занятия которых описывается распределением Бернулли, соответственно равны:
б) Распределение Эрланга используется при N>>v и имеет вид:
где 
- вероятность занятия любых i линий в пучке из v.
Y – средняя интенсивность нагрузки Y=a*v=0,45*9=4,05
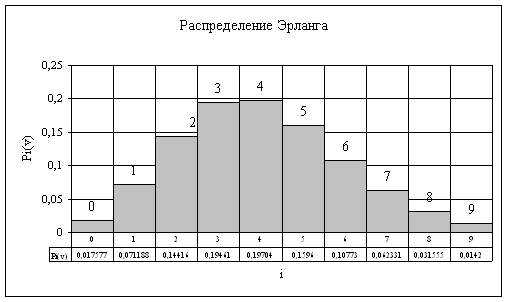
Рисунок 2 Распределение Эрланга
Математическое ожидание и дисперсия числа занятых линий, вероятность занятия которых подчиняется распределению Эрланга, соответственно равны:
в) Распределение Пуассона используется при N, v → ∞ и имеет вид:
где Y – средняя интенсивность нагрузки Y=a*v=0,45*9=4,05
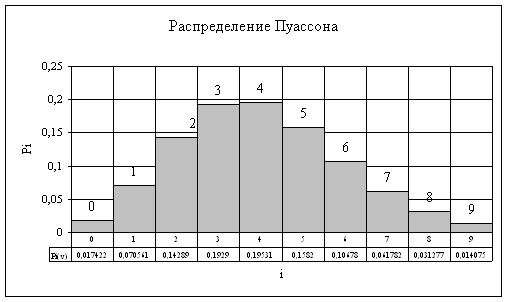
Рисунок 3 Распределение Пуассона
Математическое ожидание и дисперсия числа занятых линий, в бесконечном пучке линий равны между собой и вычисляются по формуле:
Потоки вызовов. Основные свойства и характеристики
Задание 2
На коммутационную систему поступает простейший поток вызовов с интенсивностью Y.
1. Рассчитать вероятности поступления менее k вызовов за промежуток времени [0, t*): Pk(t*), где t*= 0,5; 1,0; 1,5; 2,0.
Похожие работы
аочник: Дударев А.Ю. Преподаватель: Абилов А.В. ИЖЕВСК 2001 Задание №1., где NN – номер варианта, =5,55. , где NN – номер варианта, . , .а) - распределение Бернулли. Среднее число занятых линий: . Дисперсия: . б) - распределение Пуассона. Среднее число занятых линий и дисперсия: .в) - распределение Эрланга. Среднее число занятых линий: . Дисперсия: Задание №2., , . 3. ...
... них 10 час. – обзорные лекции, 4 час. –практические занятия, 6 час. – лабораторные работы на ЭВМ. Рабочая программа курса «Моделирование систем радиосвязи и сетей радиовещания». СОДЕРЖАНИЕ ДИСЦИПЛИНЫ 1 Введение Цели и задачи дисциплины. Основные понятия теории моделирования систем. Использование моделирования при исследовании и проектировании сетей ...
... . Требования к сельским коммутационным станциям : Требования, предъявляемые к используемому для модернизации сельских районов коммутационному оборудованию, в значительной степени обусловлены не только географическими особенностями и исторически сложившейся структурой сельских телефонных сетей (СТС), но и принятыми алгоритмами обслуживания вызовов для обеспечения приоритета междугородных ...
... из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика. 2. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ ДВУХ ТИПОВ В 1 исследовалось стационарное распределение марковского процесса, описывающего открытую сеть с многорежимными стратегиями обслуживания и ...
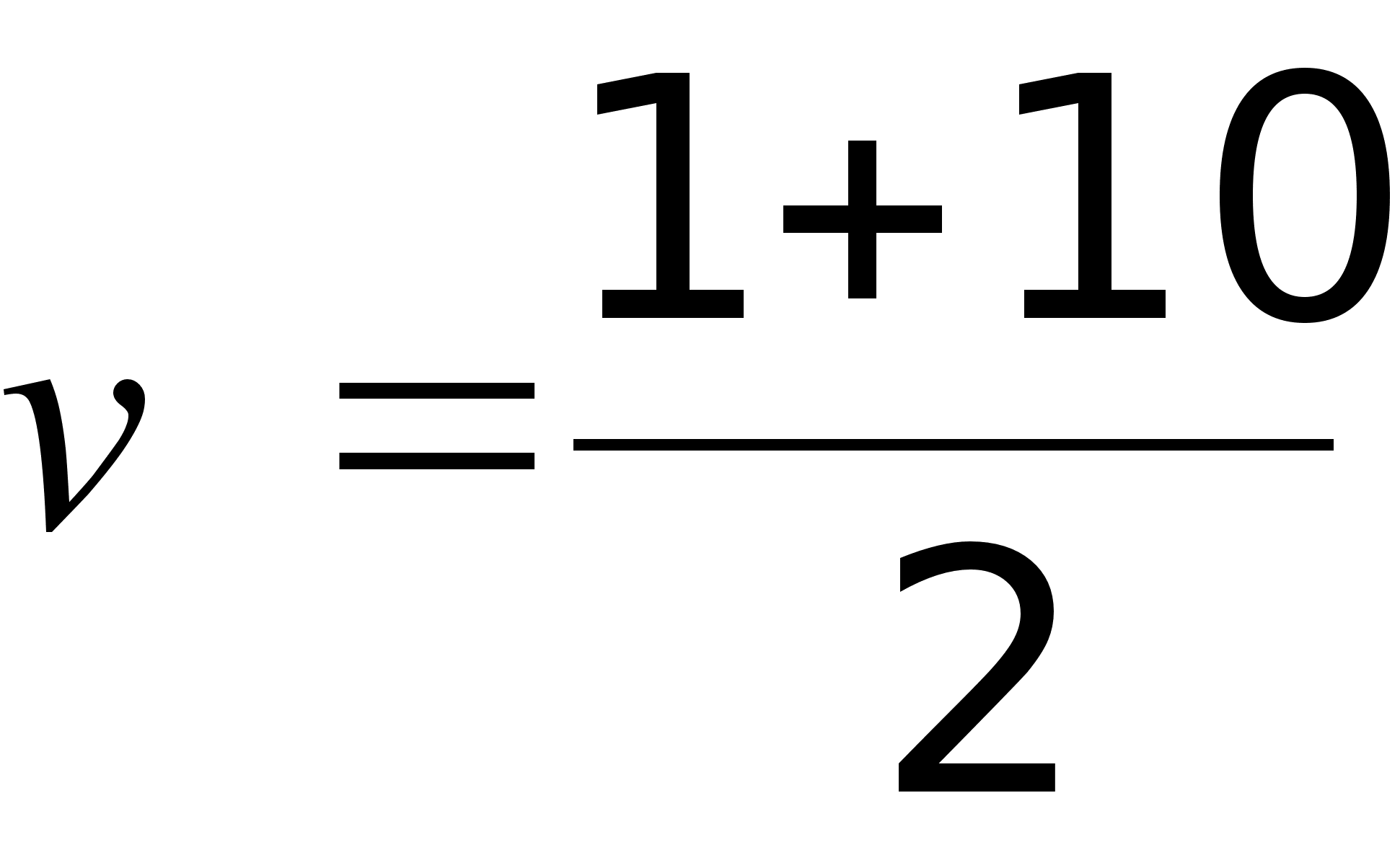
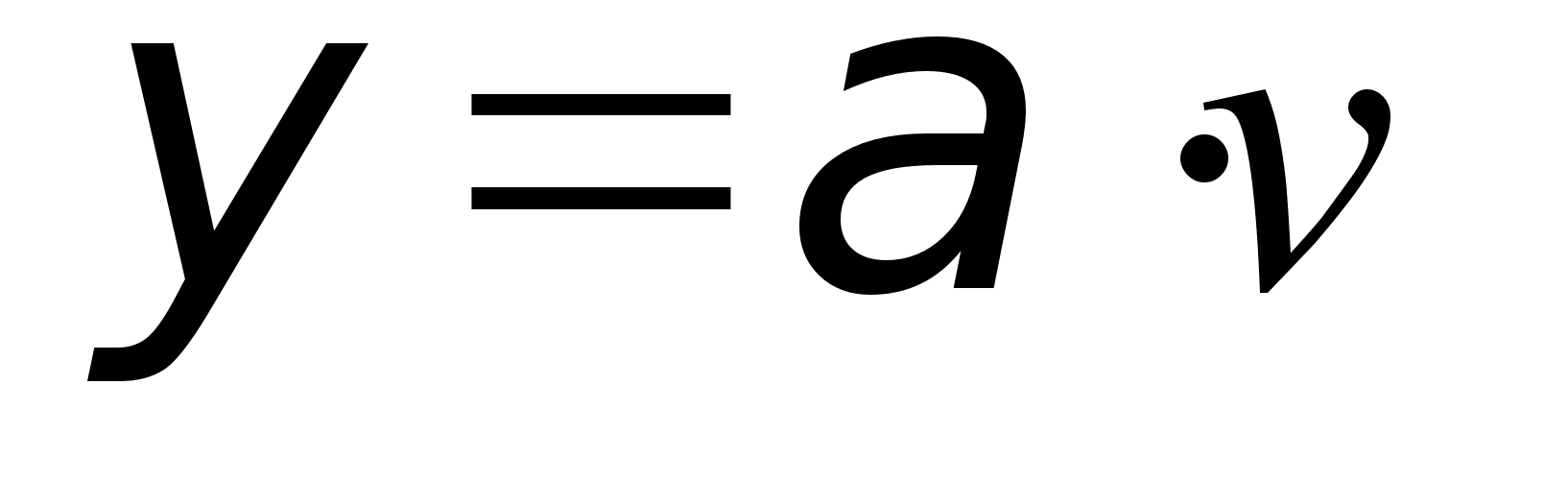
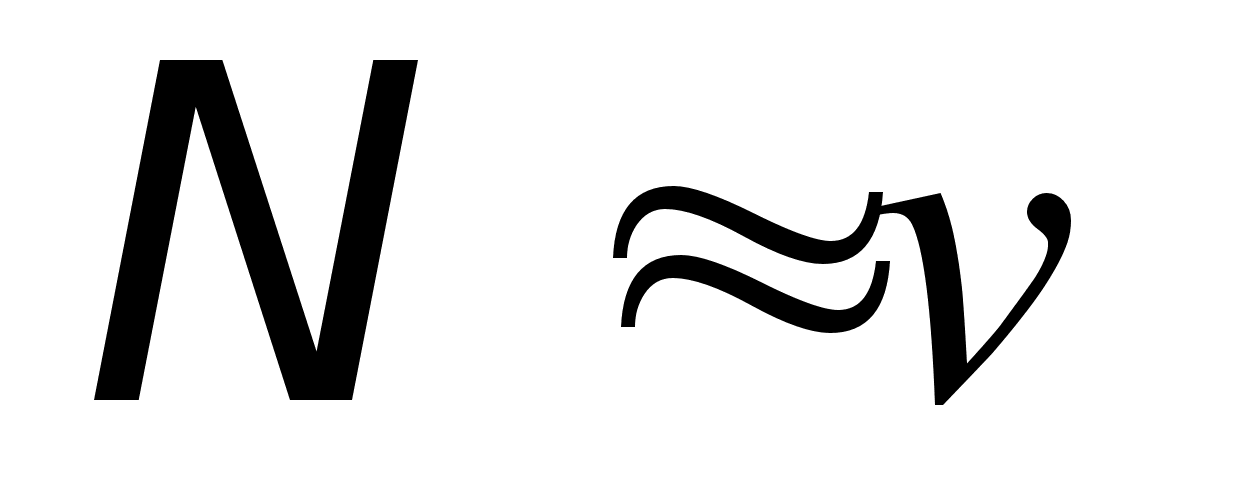
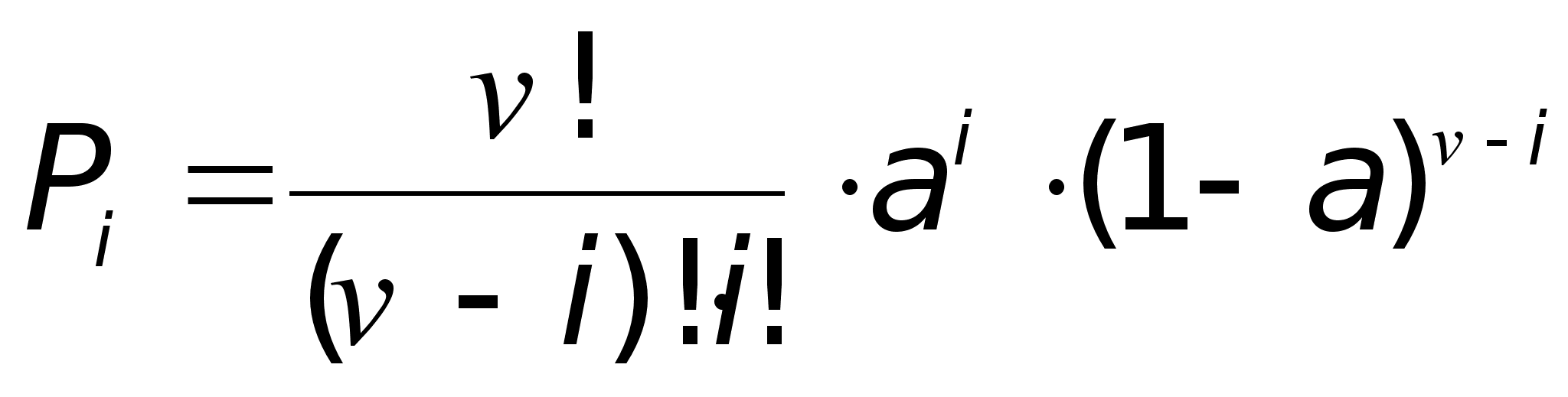
0 комментариев