Навигация
Определить расчетную интенсивность нагрузки в каждом направлении
2. Определить расчетную интенсивность нагрузки в каждом направлении.
Результаты представить в виде таблицы.
Примечание: Нагрузку на выходе 1ГИ в направлении к АМТС и УСС рассчитать следующим образом: Уамтс = 0,05 * Увых1ГИ; Уусс = 0,02 * Увых1ГИ .
Нагрузка, которая будет распределена по другим направлениям ступени, равна:
Уi = Увых1ГИ – (Уамтс + Уусс).
Для распределения нагрузки по направлениям емкости АТС взять из примечания предыдущего задания.
РешениеРаспределим нагрузку по направлениям исходящей и входящей связи. Составим диаграмму распределения нагрузки:
Нагрузка на выходе ступени 1 ГИ распределяется по направлениям исходящей связи. Нагрузку в направлении к АМТС и УСС рассчитаем следующим образом:
Уамтс = 0,05Увых1ГИ = 0,05 * 312,777 = 15,639 Эрл.
Уусс = 0,02Увых1ГИ = 0,02 * 312,777 = 6,256 Эрл.
Нагрузка, которая будет распределена по другим направлениям исходящей связи, равна:
Уi = Увых1ГИ – (Уамтс + Уусс) = 312,777 – (15,639 + 6,256) = 290,882 Эрл.
Эта нагрузка распределяется между станциями сети с помощью нормированных коэффициентов тяготения nij, которые зависят от расстояния между станциями сети Lij, эта зависимость приведена в МУ, стр.12, рис.3.
Нагрузка от проектируемой АТС к другим станциям сети может быть определена из следующей формулы: Уij = nij * Уi * Уj / (![]() nij * Уj),
nij * Уj),
Это выражение приближенно можно записать в виде: Уij = nij * Nj * Уi / (![]() nij * Nj),
nij * Nj),
Расстояние от проектируемой АТСКУ до других станций на сети выберем из условия:
1км £ Lij £ 14 км
Тогда от АТСКУ до АТСКУ1 2км., nij = 0,8;
до АТСКУ2 3км., nij = 0,75;
до АТСКУ3 4км., nij = 0,67;
до АТСКУ4 5км., nij = 0,62;
до АТСКУ5 6км., nij = 0,57;
до АТСКУ6 7км., nij = 0,52;
до АТСКУ7 8км., nij = 0,5;
При определении внутристанционной нагрузки Уij Lij = 0, а nij = 1;
Исходящую нагрузку принимаем равной входящей нагрузке, т. е.:
Уij = Уii , Увх.амтс = Уамтс.
Тогда находим:
Уii= 1*8000*290,882/[(0,8*7000)+(0,75*8000)+(0,67*6000)+(0,62*9000)+(0,57*5000)+
+(0,52*10000)+(0,5*10000)] = 67,943 Эрл.
Уатску-атску1 = 0,8 * 7000 * 0,008493 = 47,56 Эрл.;
Уатску-атску2 = 0,75 * 8000 * 0,008493 = 50,957 Эрл.;
Уатску-атску3 = 0,67 * 6000 * 0,008493 = 34,142 Эрл.;
Уатску-атску4 = 0,62 * 9000 * 0,008493 = 47,39 Эрл.;
Уатску-атску5 = 0,57 * 5000 * 0,008493 = 24,205 Эрл.;
Уатску-атску6 = 0,52 * 10000 * 0,008493 = 44,163 Эрл.;
Уатску-атску7 = 0,5 * 10000 * 0,008493 = 42,465 Эрл.;
Общая входящая нагрузка на проектируемой АТС:
Увхi = ![]() Уji + Уii = 67,943 + 47,56 + 50,957 + 34,142 + 47,39 + 24,205 + 44,163 + 42,465 =
Уji + Уii = 67,943 + 47,56 + 50,957 + 34,142 + 47,39 + 24,205 + 44,163 + 42,465 =
= 460,729 Эрл.
После определения математических ожиданий интенсивности нагрузки по всем направлениям переходим к расчетным значениям нагрузки по формуле:
Ур = У + 0,674![]() , где У – математическое ожидание интенсивности нагрузки в каждом направлении. Результаты расчета сведем в табл.3
, где У – математическое ожидание интенсивности нагрузки в каждом направлении. Результаты расчета сведем в табл.3
| Направление | Математическое ожидание Уij, Эрл. | Расчетная нагрузка Ур , Эрл. |
| АТСКУ1 | 47,56 | 52,20816 |
| АТСКУ2 | 50,957 | 55,76829 |
| АТСКУ3 | 34,142 | 38,08026 |
| АТСКУ4 | 47,39 | 52,02984 |
| АТСКУ5 | 24,205 | 27,52098 |
| АТСКУ6 | 44,163 | 48,64208 |
| АТСКУ7 | 42,465 | 46,85713 |
| Внутристанционная | 67,943 | 73,49862 |
| УСС | 6,256 | 7,941809 |
| АМТС | 15,639 | 18,30441 |
Метод расчета однозвенных полнодоступных коммутационных схем при обслуживании простейшего потока вызовов в системе с потерями. Первая формула Эрланга
Задание 51. Рассчитать необходимое число линии на всех направлениях искания : ступени 1ГИ, предполагая полнодоступное однозвенное включение при заданных нормах величины потерь. Расчетную интенсивность нагрузки взять из предыдущего задания. Результаты занести в таблицу.
2. Рассчитать и построить зависимость числа линий v и коэффициента использования h от величины интенсивности нагрузки при величине потерь Р = 0,0NN, где NN - номер варианта. Результаты расчета представить в виде таблицы и графиков v = f(Y) и h = f(Y) при Р = const.
3. Построить зависимость величины потерь Ev,v(Y) от интенсивности поступающей нагрузки при фиксированном значении числа линий в направлении к УСС. Диапазон изменения величины потерь принять от 0,0001 до 0,2 (соответствующим выбором Y). Результаты представить в виде таблицы и графика Р =f(Y) при v = const.
Решение
1.Расчет необходимого числа линий на всех направлениях искания ступени 1ГИ таб.4
Таблица 4
| Направление | Расчетная нагрузка Ур , Эрл. | Р | Ртабл. | v |
| АТСКУ1 | 52,20816 | 0,005 | 0,005 | 69 |
| АТСКУ2 | 55,76829 | 0,005 | 0,005 | 73 |
| АТСКУ3 | 38,08026 | 0,005 | 0,005 | 53 |
| АТСКУ4 | 52,02984 | 0,005 | 0,005 | 69 |
| АТСКУ5 | 27,52098 | 0,005 | 0,005 | 40 |
| АТСКУ6 | 48,64208 | 0,005 | 0,005 | 65 |
| АТСКУ7 | 46,85713 | 0,005 | 0,005 | 63 |
| Внутри-станционная | 73,49862 | 0,003 | 0,003 | 93 |
| УСС | 7,941809 | 0,001 | 0,001 | 21 |
| АМТС | 18,30441 | 0,01 | 0,01 | 28 |
2. Рассчитаем и построим зависимость числа линий v и коэффициента использования h от величины интенсивности нагрузки при величине потерь Р = 0,008 по формулам:
h = У0/v, где У0 – обслуженная нагрузка,
У0 = У – Упот = У * [1 – Еv,v(У)] = У * 0,985
Таблица 5 Результаты расчета
| №п.п. | У, Эрл. | v | Ртабл. | У0 | h |
| 1 | 1 | 5 | 0,007 | 0,985 | 0,197 |
| 2 | 3 | 9 | 0,007 | 2,955 | 0,328333 |
| 3 | 5 | 12 | 0,007 | 4,925 | 0,410417 |
| 4 | 10 | 19 | 0,007 | 9,85 | 0,518421 |
| 5 | 15 | 25 | 0,007 | 14,775 | 0,591 |
| 6 | 20 | 31 | 0,007 | 19,7 | 0,635484 |
| 7 | 25 | 37 | 0,007 | 24,625 | 0,665541 |
| 8 | 30 | 43 | 0,007 | 29,55 | 0,687209 |
| 9 | 40 | 54 | 0,007 | 39,4 | 0,72963 |
| 10 | 50 | 66 | 0,007 | 49,25 | 0,746212 |
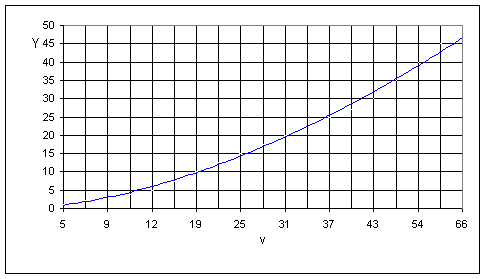
Рисунок 7 График зависимости v = f(Y)
|
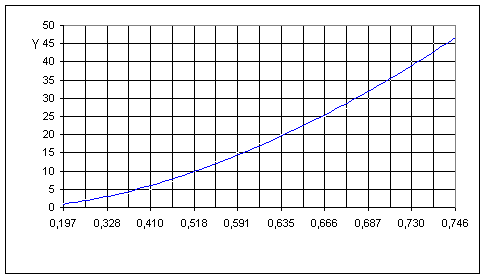
Рисунок 8 График зависимости h = f(Y)
3. Построим зависимость величины потерь Ev,v(Y) от интенсивности поступающей нагрузки при фиксированном значении числа линий в направлении к УСС.
Результаты расчета при v = const = 20 таб.6
Таблица 6
| №п.п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| У, Эрл. | 7,70 | 8,16 | 8,44 | 8,83 | 9,40 | 10,46 | 11,04 | 11,45 | 11,91 | 12,92 |
| Ртабл. | 0,0001 | 0,0002 | 0,0003 | 0,0005 | 0,001 | 0,003 | 0,005 | 0,007 | 0,01 | 0,02 |
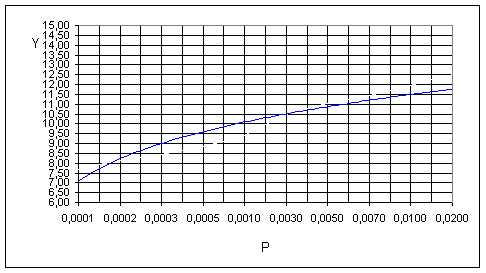
Рисунок 9 График зависимости Р =f(Y)
Метод расчета однозвенных полнодоступных коммутационных схем при обслуживании примитивного потока вызовов в системе с потерями. Первая формула Энгсета - Фрайя
Задание 61. Используя таблицы (приложение 2), рассчитать для заданных значений v и а при n = 20 вероятности Рt, Рв, Рн, сравнить их по величине. Для расчета значения v и а взять из задания 1. Если а > 0,5, то принять а = а/2.
2. Построить зависимость числа линий v от интенсивности нагрузки при фиксированном значении Рв = 0,0NN при n = 10, 30, 60. На этом же рисунке построить зависимость v = f(Y) для обслуживания простейшего потока вызовов. Результаты представить в виде таблицы. Объяснить полученные зависимости.
Решение1. Рассчитаем вероятности Рt, Рв, Рн по формулам:
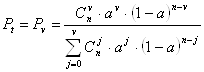 ;
;
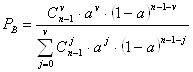 ;
;
![]() ,
,
где а = 0,5 – интенсивность нагрузки от одного источника;
v = 9 – число линий в пучке;
n = 20 – число источников нагрузки, из условия задания.
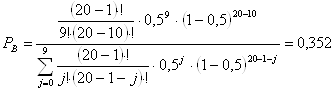 ;
;
 ;
;
![]() ;
;
По результатам расчета видно, что Рt> Рв> Рн.
2. Построим зависимость числа линий v от интенсивности нагрузки при фиксированном значении Рв = 0,0NN = 0,008 при n = 10, 30, 60. На этом же рисунке построим зависимость v = f(Y) для обслуживания простейшего потока вызовов.
Результаты расчета при Рв = 0,007 приведены в таб.7
Таблица 7
График зависимости числа линий v от интенсивности нагрузки рис.10
| №п.п. | a | Y = a*n | v |
| n = 5 | 0,5 | 2,5 | 5 |
| n = 10 | 0,5 | 5 | 9 |
| n = 20 | 0,5 | 10 | 15 |
| n = 30 | 0,5 | 15 | 22 |
| n = 40 | 0,5 | 20 | 27 |
| n = 50 | 0,5 | 25 | 33 |
| n = 70 | 0,5 | 35 | 44 |
| n = 100 | 0,5 | 45 | 61 |
| n = ∞ | 0,5 | 50 | 65 |
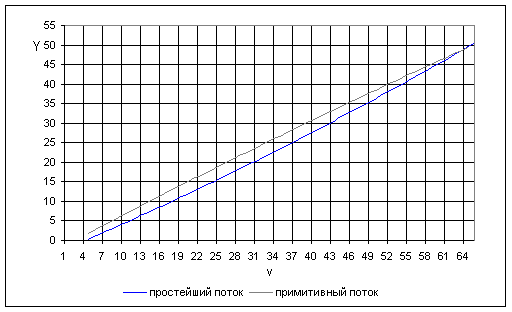
Рисунок 10 График зависимости числа линий v от интенсивности нагрузки
Характер зависимости величины поступающей нагрузки Y от емкости пучка линий, который обслуживает вызовы примитивного потока, поступающие от фиксированного числа источников n такой же, как и при обслуживании вызовов простейшего потока. Однако на пропускную способность пучка влияет число источников вызовов n: в области малых потерь с уменьшением n увеличивается пропускная способность пучка. Из выше приведенного графика видно, что при данном качестве обслуживания поступающая на v линий пучка нагрузка создаваемого вызовами примитивного потока от любого числа источников имеет большую величину по сравнению с нагрузкой Y, создаваемой вызовами простейшего потока.
Таким образом, с точки зрения величины обслуживаемой нагрузки примитивный поток всегда «лучше» простейшего потока вызовов.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Корнышев Ю. Н., Пшеничников А. П., Харкевич А. Д. Теория телетрафика - М.: Радиои связь, 1996. - 272 с.
2. Лившиц B.C., Пшеничников А.П., Харкевич А.Д. Теория телетрафика - М.: Связь, 1979. - 224 с.
3. Шнепс М.А. Системы распределения информации. Методы расчета. М.: Связь, 1979. -342 с.
4. Корнышев Ю.Н., Фань Г.Л. Теория распределения информации. М.: Радио и связь, 1985.-184 с.
5. Башарин Г.Л. Таблицы вероятностей и средних, квадратичных отклонений потерь на полнодоступном пучке линий. - М.: АН СССР 1962. -128 с.
6. Учебное пособие по курсовому проектировании координатных АТС / Р.А. Аваков, М.А. Подвида, В.Е. Родзянко- Л., 1961. - 102 с.
7. Лившиц B.C., Фидлин Л.В. Системы массового обслуживания с конечным числом источников. - М.: Связь, 1968. - 167 с.
8. Ионин Г.Л., Седол Я.Я. Таблицы вероятностных характеристик полнодоступного пучка при повторных вызовах. - М.: Наука, 1970. -155 с.
9. Захаров Т.П., Варакосин Н.П. Расчет количества каналов связи при обслуживании с ожиданием. - М.: Связь, 1967. - 194 с.
10. Проектирование координатных автоматических телефонных станций типа АТСК /М.Ф. Когш, З.С. Коханова, О.И. Панкратова и др. / ВЗЭЙС. - М.: 1969. -143 с.
11. Блинова Р.Д., Курносова Н.И. Методические указания для выполнения курсовой работы по курсу "Теория распределения информации". - М.: МТУСИ,'1994. - 26 с.
Похожие работы
аочник: Дударев А.Ю. Преподаватель: Абилов А.В. ИЖЕВСК 2001 Задание №1., где NN – номер варианта, =5,55. , где NN – номер варианта, . , .а) - распределение Бернулли. Среднее число занятых линий: . Дисперсия: . б) - распределение Пуассона. Среднее число занятых линий и дисперсия: .в) - распределение Эрланга. Среднее число занятых линий: . Дисперсия: Задание №2., , . 3. ...
... них 10 час. – обзорные лекции, 4 час. –практические занятия, 6 час. – лабораторные работы на ЭВМ. Рабочая программа курса «Моделирование систем радиосвязи и сетей радиовещания». СОДЕРЖАНИЕ ДИСЦИПЛИНЫ 1 Введение Цели и задачи дисциплины. Основные понятия теории моделирования систем. Использование моделирования при исследовании и проектировании сетей ...
... . Требования к сельским коммутационным станциям : Требования, предъявляемые к используемому для модернизации сельских районов коммутационному оборудованию, в значительной степени обусловлены не только географическими особенностями и исторически сложившейся структурой сельских телефонных сетей (СТС), но и принятыми алгоритмами обслуживания вызовов для обеспечения приоритета междугородных ...
... из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика. 2. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ ДВУХ ТИПОВ В 1 исследовалось стационарное распределение марковского процесса, описывающего открытую сеть с многорежимными стратегиями обслуживания и ...
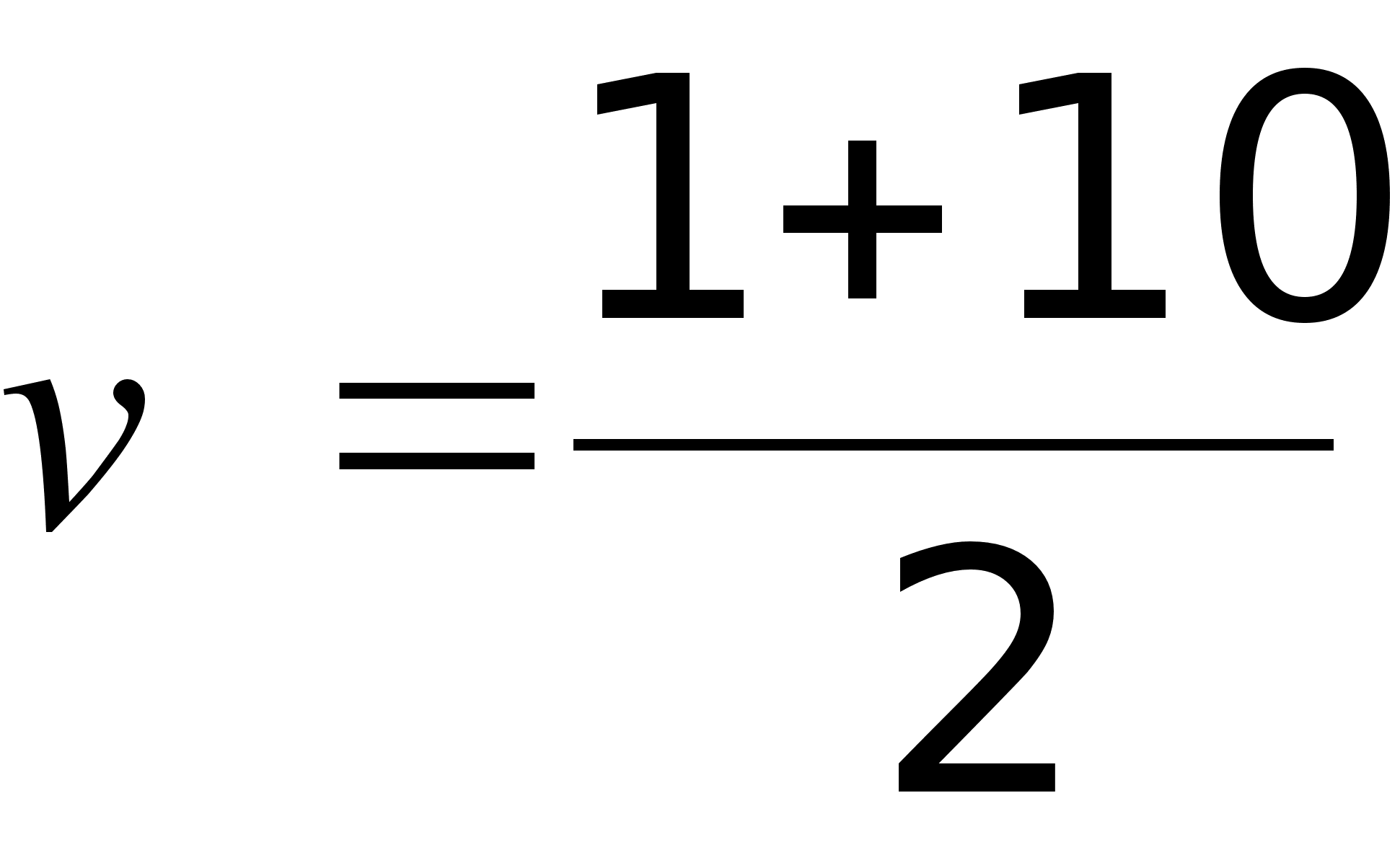
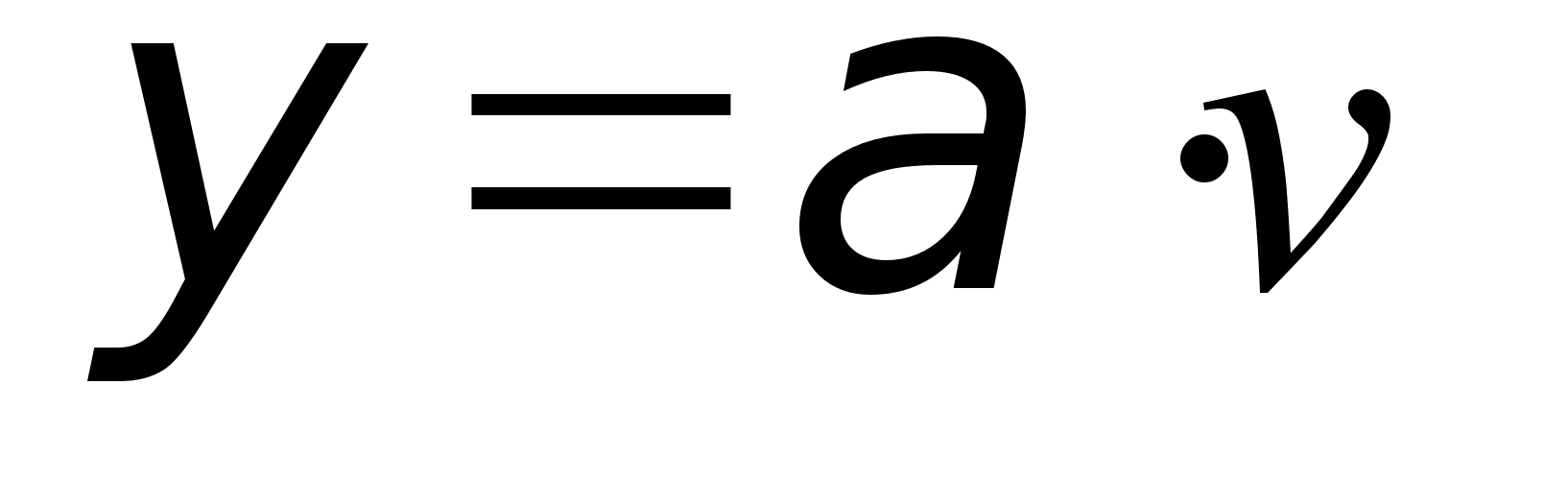
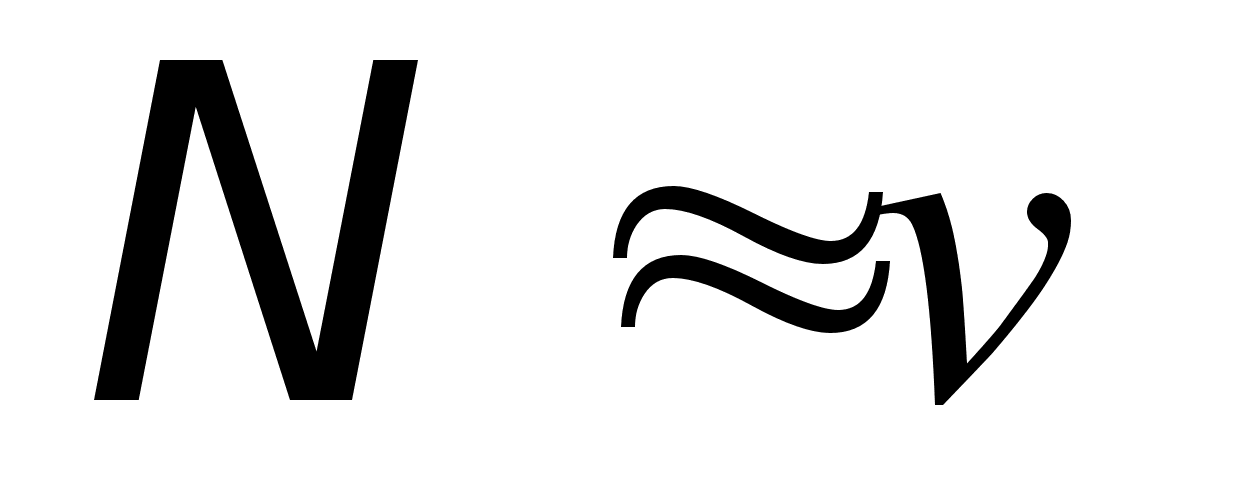
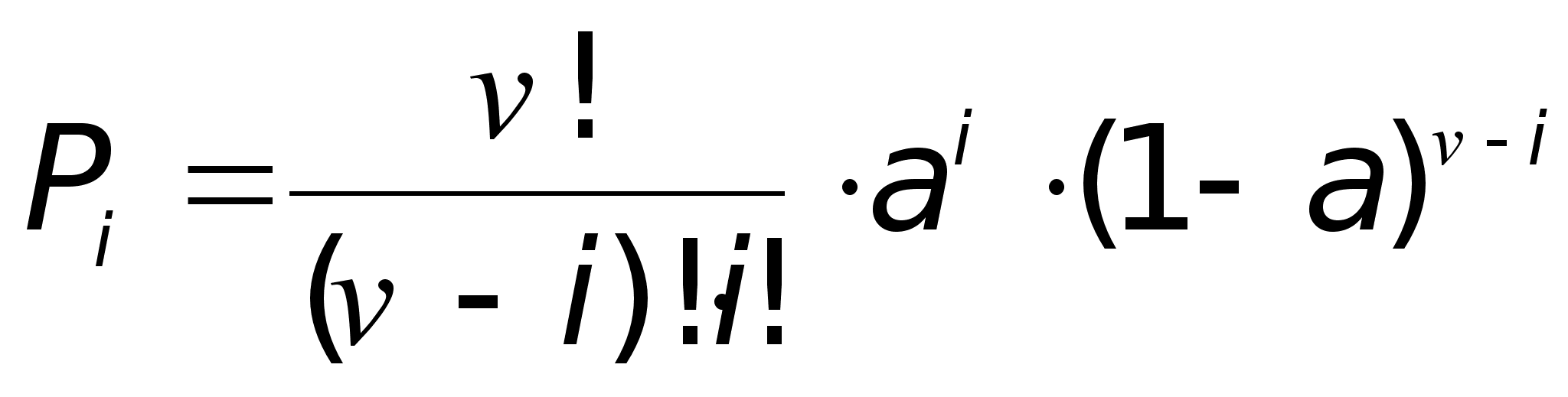

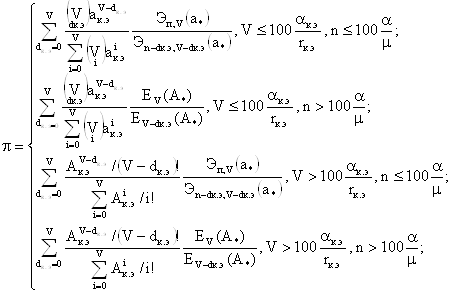

0 комментариев