Навигация
Построить функцию распределения промежутков времени между двумя последовательными моментами поступления вызовов. F(t*), где t*= 0; 0,1; 0,2;
2. Построить функцию распределения промежутков времени между двумя последовательными моментами поступления вызовов. F(t*), где t*= 0; 0,1; 0,2; ...
3. Рассчитать вероятность поступления не менее k вызовов за интервал времени [0, t*): Pi³k{t*), где t*= 1.
Примечание:
Для расчета значения Y и v взять из задания 1. Число вызовов k определить из выражения: k = [v/2] - целая часть числа.
Для построения графика, рассчитать не менее пяти значений F(t*). Результаты расчета привести в виде таблицы значений F(t*) и t*.
Расчет членов суммы Pi³k{t*) провести не менее, чем для восьми членов суммы.
Решение
1. Вероятность поступления менее k вызовов за промежуток времени [0, t*): Pk(t*), где t*= 0,5; 1,0; 1,5; 2,0; вычислим по формуле:
![]() , где k =0, 1, 2,....;
, где k =0, 1, 2,....;
Y=4,5; v=9 – из первого задания; k=v/2=9/2=4,5=5
![]()
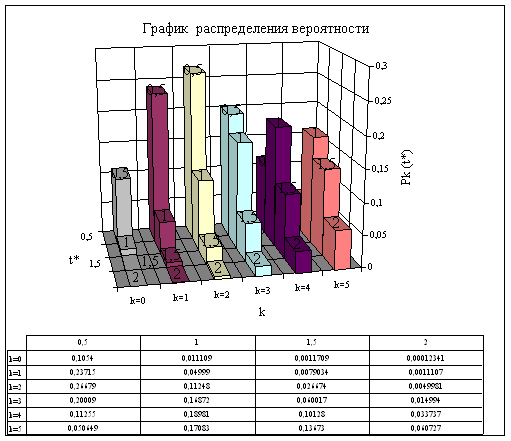
Рисунок 4 График распределения вероятности
2. Найдем и построим значения функции распределения промежутков времени между двумя последовательными моментами поступления вызовов по формуле:
![]() , где t*= 0; 0,1; 0,2; ...
, где t*= 0; 0,1; 0,2; ...
График функции распределения

Рисунок 5 График функции распределения
| t* | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| F(t*) | 0,0 | 0.362 | 0.593 | 0.741 | 0.835 | 0.895 | 0.933 | 0.957 | 0.973 | 0.983 |
Таблица 2 Результаты расчета
3. Рассчитаем вероятность поступления не менее k вызовов за интервал времени [0, t*): Pi³k{t*), где t*= 1, по формуле:
![]() ;
;
Телефонная нагрузка и ее параметры
Задание 3
1. Рассчитать интенсивность поступающей нагрузки на входы ступени 1ГИ для АТСКУ ![]() , Эрл.
, Эрл.
2. Рассчитать средние интенсивности удельных абонентских нагрузок для абонентских линии народнохозяйственного и квартирного секторов:
![]() , Эрл.;
, Эрл.;
![]() , Эрл.;
, Эрл.;
а также среднюю удельную интенсивность нагрузки на абонентскую линию АТС:
![]() , Эрл.;
, Эрл.;
Пересчитать интенсивность нагрузки на выход ступени 1ГИ.
Примечания:
Похожие работы
аочник: Дударев А.Ю. Преподаватель: Абилов А.В. ИЖЕВСК 2001 Задание №1., где NN – номер варианта, =5,55. , где NN – номер варианта, . , .а) - распределение Бернулли. Среднее число занятых линий: . Дисперсия: . б) - распределение Пуассона. Среднее число занятых линий и дисперсия: .в) - распределение Эрланга. Среднее число занятых линий: . Дисперсия: Задание №2., , . 3. ...
... них 10 час. – обзорные лекции, 4 час. –практические занятия, 6 час. – лабораторные работы на ЭВМ. Рабочая программа курса «Моделирование систем радиосвязи и сетей радиовещания». СОДЕРЖАНИЕ ДИСЦИПЛИНЫ 1 Введение Цели и задачи дисциплины. Основные понятия теории моделирования систем. Использование моделирования при исследовании и проектировании сетей ...
... . Требования к сельским коммутационным станциям : Требования, предъявляемые к используемому для модернизации сельских районов коммутационному оборудованию, в значительной степени обусловлены не только географическими особенностями и исторически сложившейся структурой сельских телефонных сетей (СТС), но и принятыми алгоритмами обслуживания вызовов для обеспечения приоритета междугородных ...
... из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика. 2. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ ДВУХ ТИПОВ В 1 исследовалось стационарное распределение марковского процесса, описывающего открытую сеть с многорежимными стратегиями обслуживания и ...
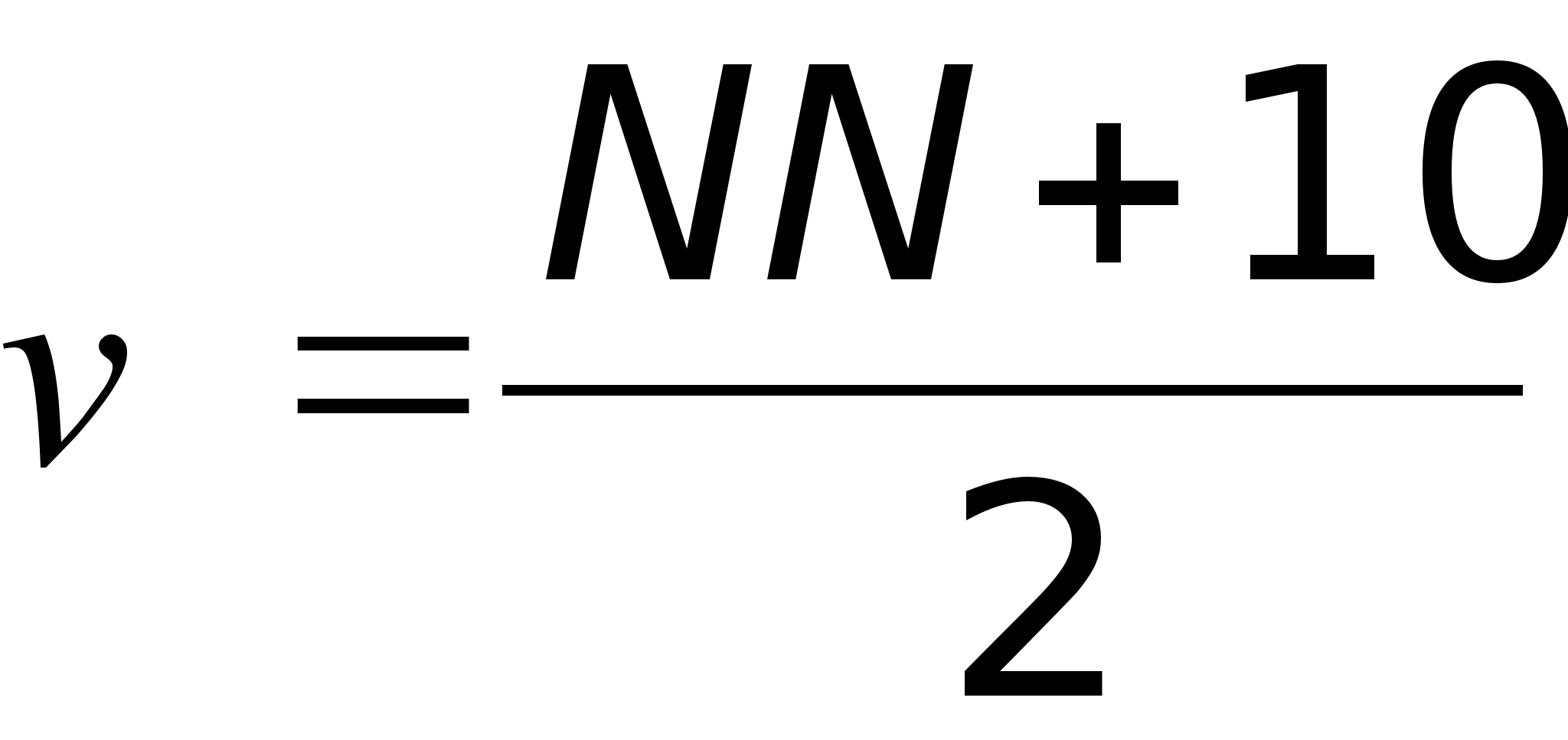
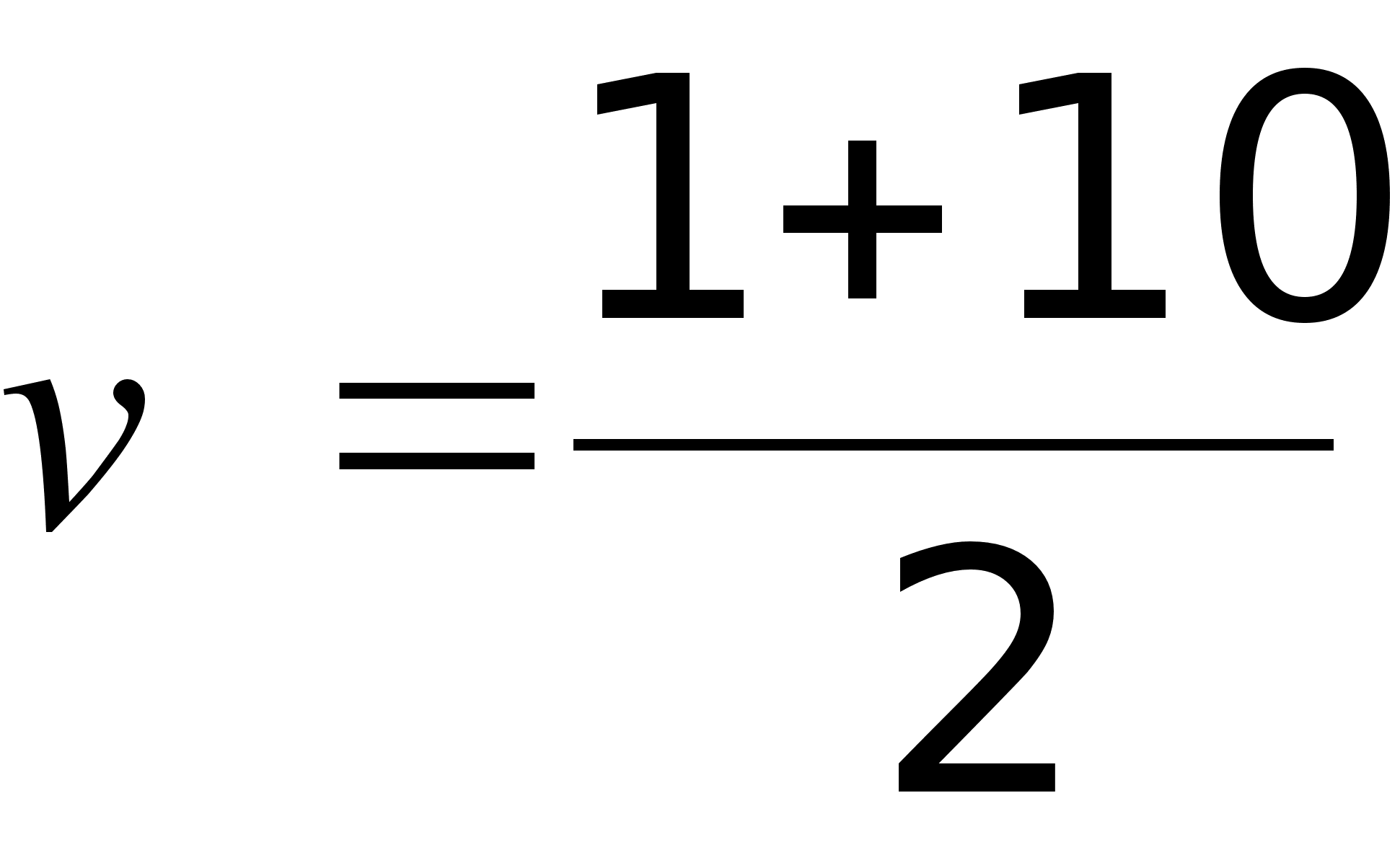
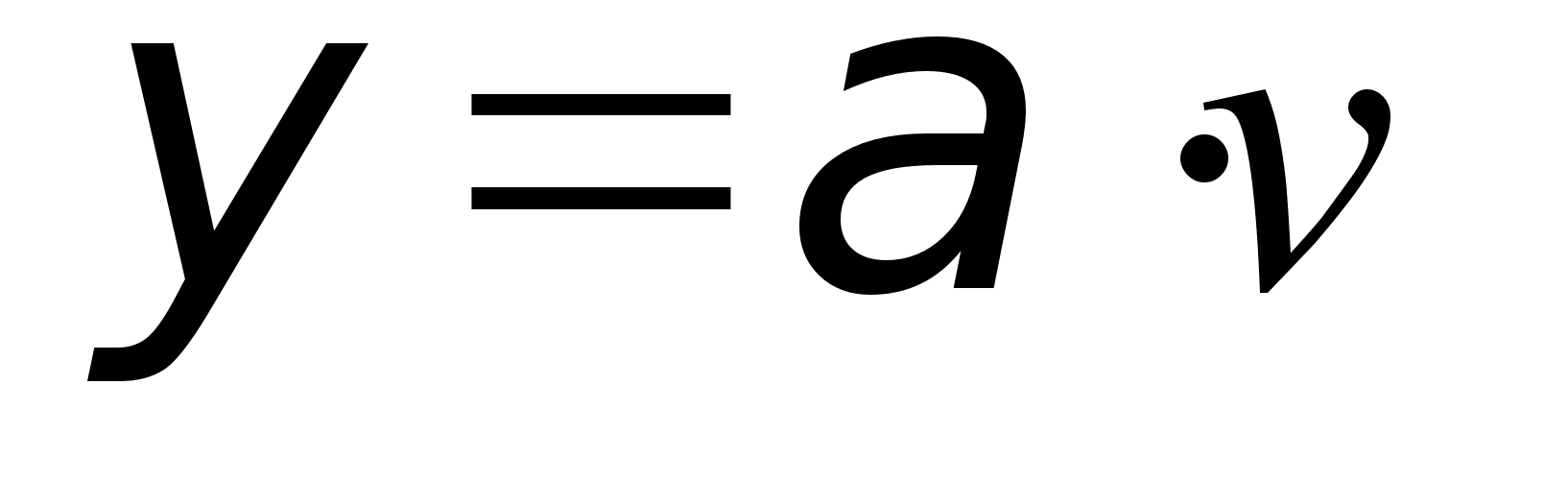
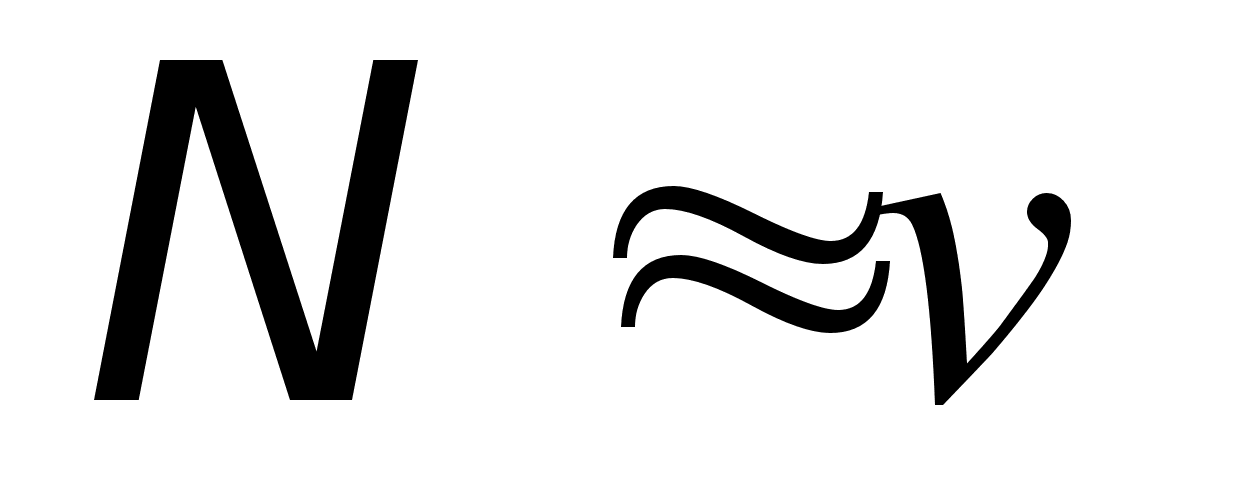
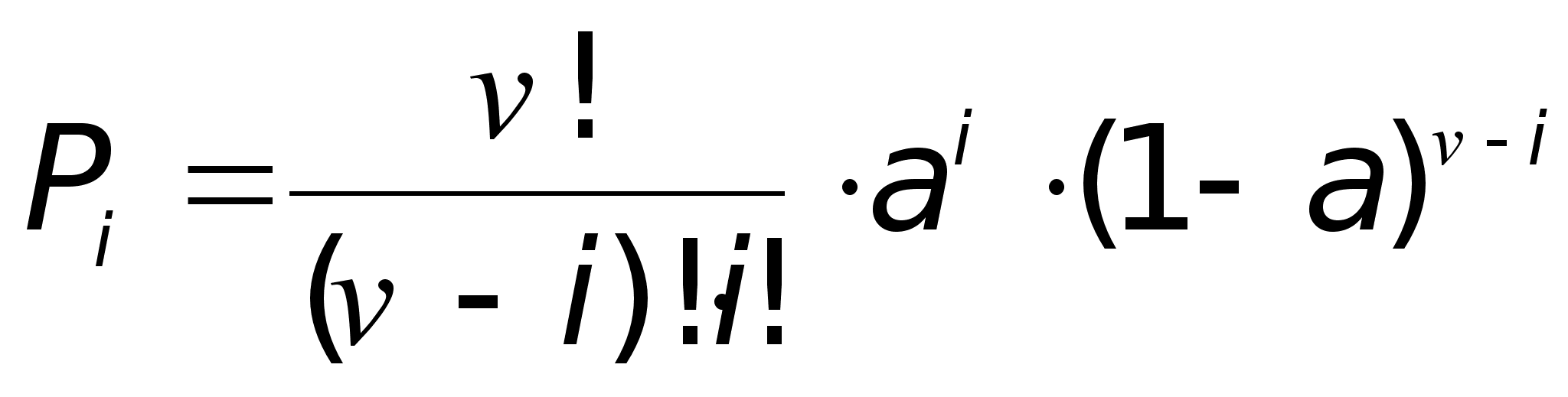

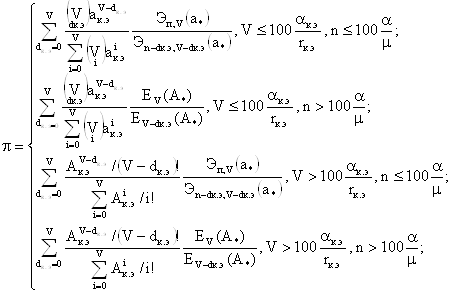

0 комментариев