Навигация
Фильтры нижних частот. Общий случай
1.5 Фильтры нижних частот. Общий случай
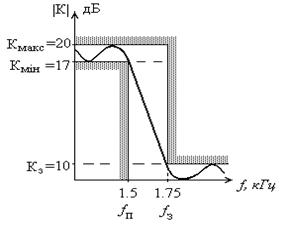
Фильтр нижних частот представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы высоких частот. В общем случае определим полосу пропускания как интервал частот 0<w<wс, полосу задерживания как частоты w>w1 переходную область как диапазон частот wc<w<w1 (wc – частота среза). Эти частоты обозначены на рис. 1.5.1, на котором приведена реальная амплитудно-частотная характеристика фильтра нижних частот, где в данном случае заштрихованные области представляют собой допустимые отклонения характеристики в полосах пропускания и задерживания.
Если минимальное затухание выбрать за нормированный уровень 0 (А =1 на рис. 2.1), то логарифмическая характеристика фильтра нижних частот имеет вид, изображенный на рис. 1.5.2. Максимальное затухание в децибелах в полосе пропускания составляет α1, а минимальное затухание в полосе задерживания α2 (А1 и А2 – соответственно значения амплитудно-частотной характеристики). Затухание α1 не может превышать 3 дБ, в то время как типовое значение α2 значительно больше и может находиться в пределах от 20 до 100 дБ.
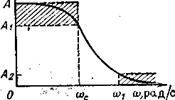
Рис. 1.5.1 Реальная амплитудно-частотная характеристика фильтра нижних частот
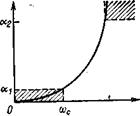
Рис. 1.5.2. Логарифмическая характеристика: фильтра нижних частот
Коэффициент усиления фильтра нижних частот представляет собой значение его передаточной функции при s=0 или, что эквивалентно, значение его амплитудно-частотной характеристики на частоте w=0. Следовательно, коэффициент усиления реального фильтра с амплитудно-частотной характеристикой, показанной на рис. 1.5.1, равен А.
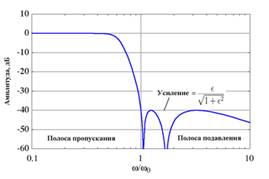
Существует много типов фильтров нижних частот, удовлетворяющих данному набору технических требований, таких, как А, А1 A2, wc и w1 обозначенных на рис. 1.5.1, или α1, α2, wcи w1 – на рис. 1.5.2. Фильтры Баттерворта, Чебышева, инверсные Чебышева и эллиптические образуют четыре наиболее известных класса. Фильтр Баттерворта обладает монотонной характеристикой, подобной характеристике на рис. 1.5.1 и 1.5.2. (Характеристика является монотонно спадающей, если она никогда не возрастает с увеличением частоты.) Характеристика фильтра Чебышева содержит пульсации (колебания передачи) в полосе пропускания и монотонна в полосе задерживания. На рис. 1.5.3 изображен вид характеристики фильтра Чебышева шестого порядка. Инверсная характеристика фильтра Чебышева монотонна в полосе пропускания и обладает пульсациями в полосе задерживания. Пример характеристики фильтра шестого порядка приведен на рис. 1.5.4.
Амплитудно-частотная характеристика оптимального фильтра нижних частот удовлетворяет обозначенным на рис. 1.5.1 (или на рис. 1.5.2) условиям для данного порядка п и допустимого отклонения в полосах пропускания и задерживания при минимальной ширине переходной области. Таким образом, если заданы значения A, A1, А2, n и wc, то значение частоты w1 минимально. Для полиномиальной характеристики оптимальной является характеристика фильтра Чебышева. Однако в общем случае оптимальным является эллиптический фильтр, характеристики которого значительно лучше характеристик фильтра Чебышева.
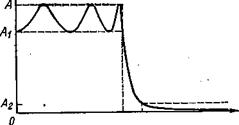
Рис. 1.5.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка
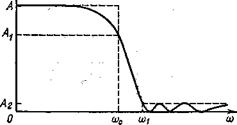
Рис. 1.5.4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка
1.6 Фильтры нижних частот на ИНУН
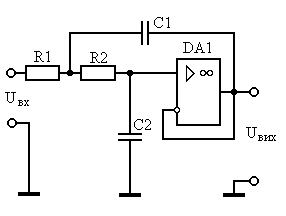
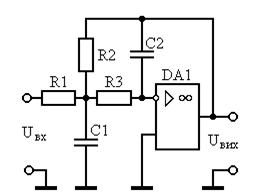
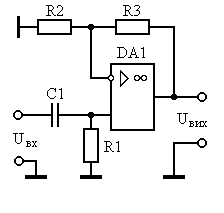
Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта или Чебышева второго порядка вида
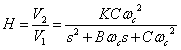
изображена на рис. 1.6. Анализируя эту схему, получаем:
![]() ;
;
![]() ; (1.4)
; (1.4)
![]() .
.
Значения сопротивлений определяются следующим образом:
![]() ;
;
![]() ;
;
![]() ; (1.5)
; (1.5)
![]() .
.
где С2 имеет предпочтительно близкое к значению 10/fс мкФ.
А С1 должно удовлетворять следующему неравенству
![]()
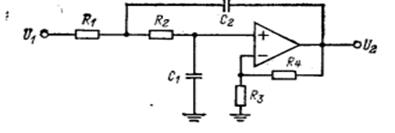
Рис. 1.6. Схема фильтра нижних частот на ИНУН
1.7 Расчет фильтра нижних частот на Инун
Для расчета фильтра нижних частот или Чебышева более высокого порядка, обладающего заданной частотой среза fс (Гц), или wс =2πfс и коэффициентом усиления К = 1, необходимо выполнить следующие шаги.
1. Найти нормированные значения коэффициентов нижних частот В и С из соответствующей таблицы в приложении А.
2. Выбрать номинальное значение емкости С2 (предпочтительно близкое к значению 10/f мкФ) и вычислить значения сопротивлений по (1.5)
3. Выбрать номинальные значения, наиболее близкие к вычисленным значениям, и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 1.6.
2. Техническое задание
1. Фильтр Чебышева верхних частот на ИНУН;
2. Порядок N = 6;
3. Коэффициент усиления К = 8;
4. Частота среза fc = 100 Гц;
5. Неравномерность передачи в полосе пропускания PRW = 1.0 дБ;
6. Использование резисторов и конденсаторов ряда Е96.
3. Расчеты
Один из популярных способов построения фильтра заключается в том, чтобы представить передаточную функцию в виде произведения сомножителей H1, H2,…, Нm и создать схемы или звенья, или каскады N1, N2,…, Nm, соответствующие каждому сомножителю. Эти звенья соединяются между собой каскадно, выход первого является входом второго и т.д. Если эти звенья не будут влиять друг на друга и не будут изменять собственные передаточные функции, то общая схема обладает требуемой передаточной функцией n-го порядка.
Разобьем фильтр 6-ого порядка на 3 звена 2-ого порядка. Так как общий коэффициент усиления должен быть равен 8, то все наши звенья будут одинаковы с коэффициентом усиления 2 каждое.
Каждое звено будет иметь передаточную функцию вида
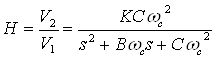
Нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам») для параметров: общий порядок N = 6, неравномерности передачи, в полосе пропускания PRW = 1,0 дБ.
| В | С | |
| I звено | 0.124362 | 0.990732 |
| II звено | 0.339763 | 0.55772 |
| III звено | 0.464125 | 0.124707 |
Порядок звена равен N = 2. Коэффициент усиления К1 = 2.
1) Найдем нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам»).
| В | С | |
| I звено | 0.124362 | 0.990732 |
2) Вычисляем значение элементов C1, C2, R1, R2, R3, R4, по формулам:
Находим значение емкости С2 близкое к величине ![]() , т.е. С2 = 0.1 мкФ.
, т.е. С2 = 0.1 мкФ.
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Откуда получаем теоретические значение элементов для первого звена
| С1, нФ | R1, кОм | R2, кОм | R3, кОм | R4, кОм | |
| Теоретические значения элементов для I звена | 100 | 256 | 0.995 | 514 | 514 |
Из уравнений
![]() ;
;
![]() ;
;
![]() .
.
Находим коэффициенты для передаточной функции
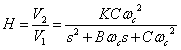
|
|
|
| |
| I звена | 2 | 78.137 | 391100 |
С учетом того, что ![]() определяем передаточную функцию первого звена
определяем передаточную функцию первого звена
![]()
Таким образом, ![]() – модуль передаточной функции – АЧХ первого звена, а
– модуль передаточной функции – АЧХ первого звена, а ![]() – аргумент передаточной функции – ФЧХ первого звена.
– аргумент передаточной функции – ФЧХ первого звена.
АЧХ первого звена
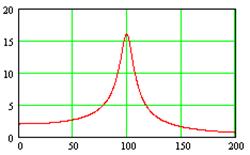
ФЧХ первого звена
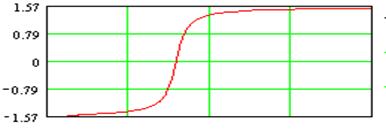
Порядок звена равен N = 2. Коэффициент усиления К2 = 2
1) Найдем нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам»).
| В | С | |
| II звено | 0.339763 | 0.55772 |
2) Вычисляем значение элементов C1, C2, R1, R2, R3, R4, по формулам:
| С1, нФ | R1, кОм | R2, кОм | R3, кОм | R4, кОм | |
| Теоретические значения элементов для II звена | 105 | 93.69 | 4.6 | 196.6 | 196.6 |
Из уравнений находим коэффициенты для передаточной функции
|
|
|
| |
| II звена | 2 | 213.473 | 220200 |
Подставляя данные коэффициенты в получаем передаточную функцию для второго звена
![]()
Таким образом, ![]() – модуль передаточной функции – АЧХ второго звена, а
– модуль передаточной функции – АЧХ второго звена, а ![]() – аргумент передаточной функции – ФЧХ второго звена.
– аргумент передаточной функции – ФЧХ второго звена.
АЧХ второго звена
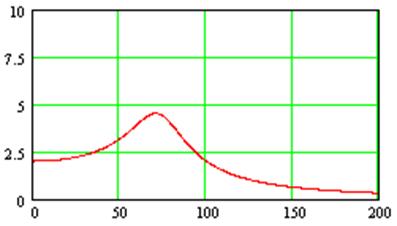
ФЧХ второго звена
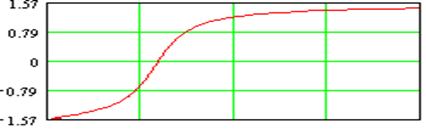
Порядок звена равен N = 2. Коэффициент усиления К3 = 2
2) Найдем нормированные значения коэффициентов В, С из приложения А (в книге Д. Джонсон, Дж. Джонсон «Справочник по активным фильтрам»).
| В | С | |
| III звено | 0.464125 | 0.124707 |
2) Вычисляем значение элементов C1, C2, R1, R2, R3, R4, по формулам:
| С1, нФ | R1, кОм | R2, кОм | R3, кОм | R4, кОм | |
| Теоретические значения элементов для III звена | 143 | 68.58 | 20.68 | 178.5 | 178.5 |
Из уравнений находим коэффициенты для передаточной функции
|
|
|
| |
| III звена | 2 | 291.61 | 49230 |
Подставляя данные коэффициенты в получаем передаточную функцию для второго звена
![]()
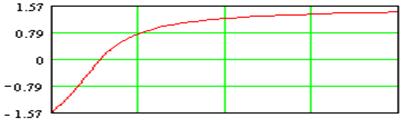
Таким образом, ![]() – модуль передаточной функции – АЧХ второго звена, а
– модуль передаточной функции – АЧХ второго звена, а ![]() – аргумент передаточной функции – ФЧХ второго звена.
– аргумент передаточной функции – ФЧХ второго звена.
АЧХ третьего звена
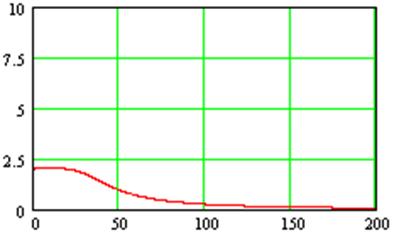
ФЧХ третьего звена
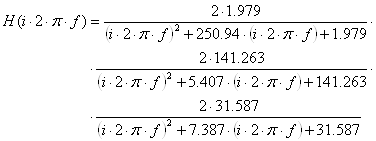
Итоговая передаточная характеристика будет представлять собой произведение сомножителей H1, H2, Н3:
![]()
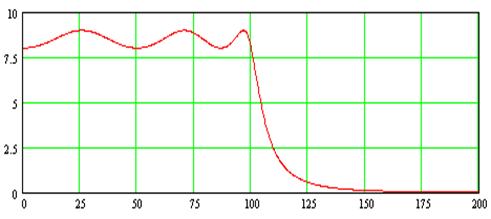
АЧХ фильтра (теоретическая)
Выберем номинальные значения элементов из ряда Е96, наиболее близкие к вычисленным значениям
I звено
| С1, нФ | R1, кОм | R2, кОм | R3, кОм | R4, кОм | |
| Номинальные Значения элементов для I звена | 100 | 255 | 1.0 | 511 | 511 |
II звено
| С1, нФ | R1, кОм | R2, кОм | R3, кОм | R4, кОм | |
| Номинальные Значения элементов для II звена | 105 | 93.1 | 4.64 | 196 | 196 |
III звено
| С1, нФ | R1, кОм | R2, кОм | R3, кОм | R4, кОм | |
| Номинальные Значения элементов для III звена | 143 | 68.1 | 20.5 | 178 | 178 |
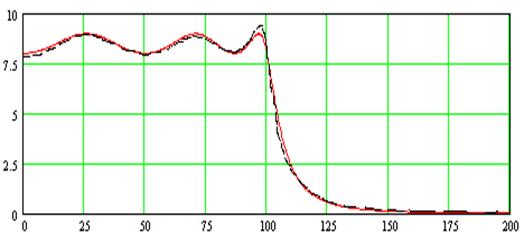
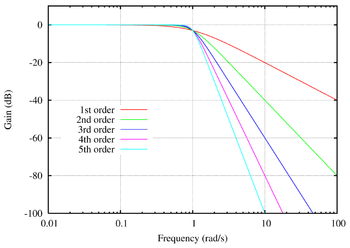
С учетом номиналов резисторов и конденсаторов из ряда Е96, получим следующую АЧХ (сплошной линией показана характеристика с учетом номиналов ряда Е96, пунктирной линией – теоретическая характеристика).
Вследствие того, значения из ряда Е96 не сильно расходятся с рассчитанными, мы получаем практически ожидаемую АЧХ. (Пунктиром обозначен АЧХ реальный)
Литература
1. Джонсон Д., Джонсон Дж., Мур Г. Справочник по активным фильтрам. Пер. с англ. – М.: Энергоатомиздат, 1983.
2. Остапенко Г.С. Усилительные устройства. Учебн. пособие для вузов. – М.: Радио и связь, 1989.
3. Альфа-Электроник. Резисторы. Обозначения и параметры. [Интернет-ресурс]
Похожие работы
... Сравнительная характеристика различных реализаций синтезируемого фильтра. 17 Литература..................................................................................................................................................................... 18 Задание 1. Представить данные на синтез частотно-избирательного фильтра в графической форме с использованием нормированной ...
... соединения ФНЧ- ІІ, как на рис. 2.2: Рисунок 2.2 – Структурная схема графа Мезона Выбор схемного решения Схемным решением для данного устройства будет фильтр низкой частоты второго порядка с многопетлевой обратной связью, т.к. он обеспечивает небольшую чувствительность к отклонению номиналов элементов. Используем 3 таких звена, соединённых последовательно. Рисунок 2.3 – ФНЧ-ІІ с ...
... случае a характеризует затухание. Например, предположим, что на рис. 2 выбрано A=1, которому соответствует a=0. Тогда если то затухание на частоте wc a1=-20´lg(1/20,5)=10´lg2=3 дБ. активный полосовой фильтр частотный В основном пропускание в полосе пропускания никогда не превышает 3 дБ. Таким образом, из приведенного примера следует, что значение АЧХ в полосе пропускания ...
... (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1МГц), за пределами частотного диапазона большинства ОУ широкого применения. Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном ...

0 комментариев