Определить потребное значение емкости, рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности

5.  Определить потребное значение емкости, рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности.

В условиях данной задачи неизвестной величиной является только емкость, которую достаточно просто можно найти из уравнения передаточной функции. Однако, в интересах общности изложения последующего материала воспользуемся передаточной функцией в параметрической форме (2.14), из которой найдем значение приведенной частоты n₂, на которой передаточная функция (2.12) принимает заданное значение H₁:

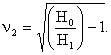
Очевидно, что (2.14) имеет смысл только при H₁<H₀.

Теперь формулу (2.11) можем записать в виде

откуда находим потребное значение емкости для построения ФНЧ-1 Рис.3.2:

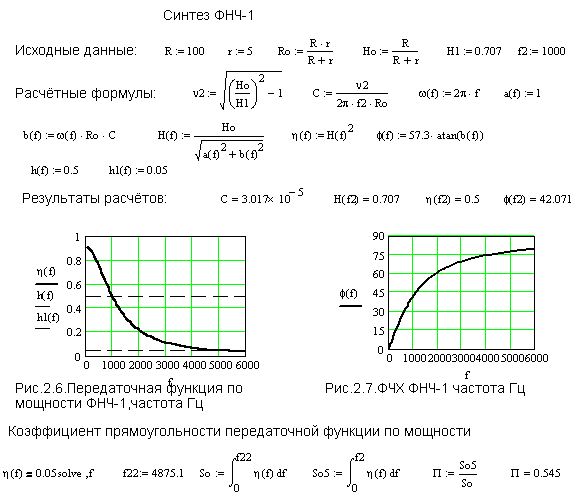
Пример 2.2. Спроектировать ФНЧ-1 Рис.2.3 при следующих исходных данных:

R=100 Ом – сопротивление нагрузки;

r=5 Ом – внутреннее сопротивление источника;

f₂=1000 Гц – верхняя граница полосы пропускания;

H₁=H(f₂)=0,707 – значение передаточной функции на верхней границе полосы пропускания;

h₁=h(f₂)=0,5 - значение передаточной функции по мощности на верхней границе полосы пропускания.

Рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности.

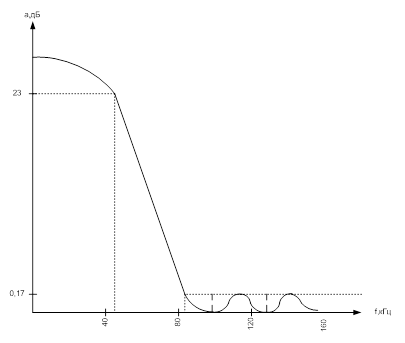
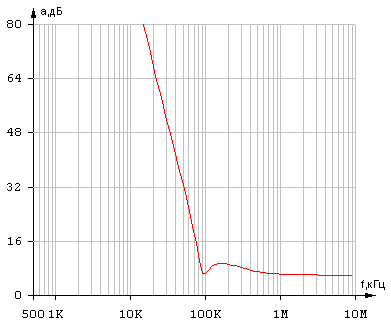
Результаты расчетов представлены на Рис.2.6 и Рис.2.7.

Из этих рисунков видно, что на верхней границе полосы пропускания f₂=1000 Гц передаточная функция по мощности h(f₂)=0,5, что соответствует требованиям технического задания.

Сдвиг фаз между входным и выходным напряжениями F(f₂)=42,071 град. Коэффициент прямоугольности передаточной функции по мощности составляет П=0,545.

Потребное значение емкости для построения ФНЧ-1 Рис.3.2 составляет С=30,17 мкФ.

2.5 Г-образный фильтр нижних частот (ФНЧ-2)

2.5.1 Частотные характеристики ФНЧ-2

В целях повышения коэффициента прямоугольности передаточной функции по мощности применяют фильтры нижних частот второго порядка, в состав которых входят два реактивных элемента: L и C.

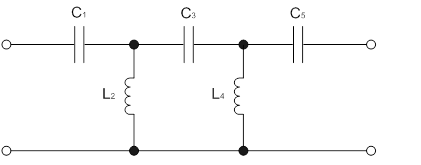
Рассмотрим Г-образный ФНЧ, схема которого представлена на Рис.2.8 (см.также Рис.1.6).

L

Z₁

Z₂ C R

Рис.2.8. Электрическая схема Г-образного ФНЧ

Работа Г-образного ФНЧ:

при

при

На малых частотах индуктивное сопротивление мало, а емкостное сопротивление велико, поэтому ток проходит в нагрузку с малым ослаблением, не ответвляясь в емкость.

На больших частотах индуктивное сопротивление велико, а емкостное сопротивление мало. Ток, прошедший через индуктивность, закорачивается емкостью. Поэтому выходное напряжение мало.

Определим АЧХ и ФЧХ Г-образного ФНЧ, рассматривая его как Г-образный 4х-П, нагруженный активным сопротивлением R.

Комплексные сопротивления плеч фильтра:

Коэффициенты формы А:

Уравнение связи входного и выходного напряжений (1.6) принимает вид:

Обозначим, как и ранее, действительную и мнимую части (2.16):

 - действительная часть;

 - мнимая часть.

Уравнение (2.16) запишем в виде:

Фазочастотная характеристика ФНЧ-2 определяется по формуле:

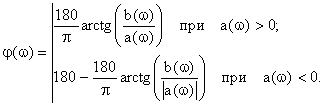
Комплексная передаточная функция по напряжению определяется из (2.17):

Модули передаточных функций по напряжению и мощности принимают вид:

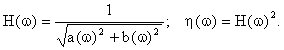
Таким образом, при известных значениях R, L, C-элементов, по формулам (2.18), (2.20) можно рассчитать и построить графики АЧХ и ФЧХ Г-образного ФНЧ.

С целью общего анализа частотных характеристик Г-образного ФНЧ представим передаточные функции (2.20) в параметрической форме, для чего обозначим:

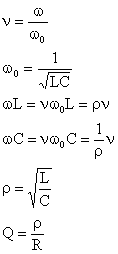
После подстановки обозначений в (2.20) получим передаточные функции в параметрической форме:

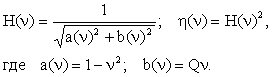
Пример 2.3. Рассчитать и построить семейство кривых передаточной функции по мощности в параметрической форме для трех значений коэффициента нагрузки:

Определить коэффициент прямоугольности передаточной функции по мощности при

Расчет передаточной функции по мощности, выполненный по формуле (2.21) приведен на Рис.2.9.

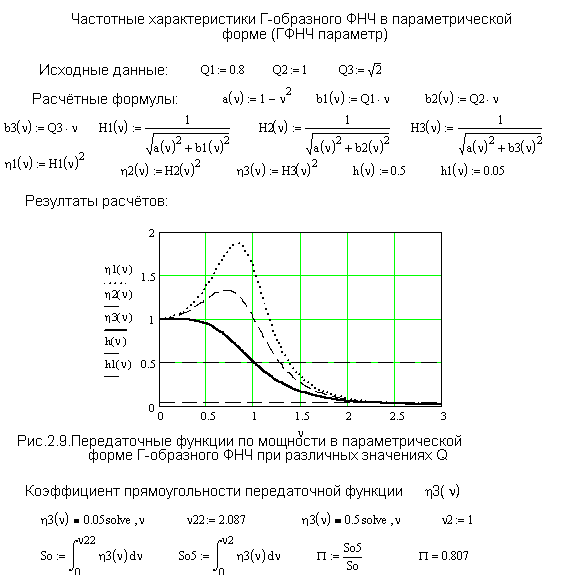
Из Рис.2.9 следует, что при Q₁=0,8 передаточная функция  достигает своего максимума, равного 1,86, а затем плавно уменьшается, Этот всплеск передаточной функции может быть желательным или нежелательным в зависимости от конкретного назначения фильтра.

При Q₂=1 всплеск передаточной функции  значительно меньше и при  он вовсе отсутствует.

Таким образом, характер изменения передаточной функции  Г-образного ФНЧ целиком определяется значением коэффициента нагрузки Q, который, в свою очередь, зависит от комбинации значений RLC-элементов. Следовательно, путем соответствующего выбора LC-элементов можно изменить форму кривой передаточной функции.

Коэффициент прямоугольности передаточной функции по мощности при  составляет П=0,807, что значительно больше, чем у ФНЧ-1.

2.5.2 Синтез Г-образного фильтра нижних частот

Техническое задание на проектирование Г-образного ФНЧ формулируется следующим образом.

1.  Спроектировать Г-образный ФНЧ, схема которого представлена на Рис.2.8.

2.  На вход фильтра подаются сигналы синусоидальной формы, частота которых изменяется от нуля до бесконечности.

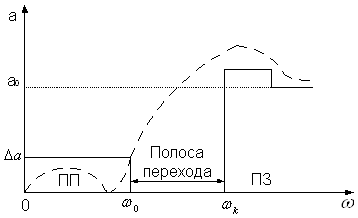
3.  Передаточные функции по напряжению и мощности в полосе пропускания (0…f₂), должны быть максимально плоскими, т.е. не иметь всплесков, превышающих единицу, и на верхней границе полосы пропускания должны принимать значения .

Похожие работы

Разработка эквивалентных и принципиальных схем электрического фильтра и усилителя напряжения

Скачать

26569

1

12

... курсовой работе, в соответствии с заданием, необходимо решить следующие задачи: - разработать (любым методом) эквивалентную, принципиальную схемы электрического фильтра на любых радиокомпонентах; - разработать усилитель напряжения на любых радиоэлементах (схему электрическую принципиальную); - любым методом рассчитать спектр сложного периодического сигнала, подаваемого с “генератора импульсов” ...

Расчет электрических фильтров

Скачать

18322

2

12

... методов синтеза электрических цепей, и в частности электрических фильтров, достигнуто в результате применения ЭВМ и разработки специальных методов расчета. В настоящее время электрические фильтры реализуются не только в виде электрических цепей с катушками индуктивности и конденсаторами, но также практическое применение получили кварцевые, электромеханические, активные RС - фильтры и другие. По ...

Условия фильтрации для реактивных лестничных четырехполюсников

Скачать

9504

0

15

... , как показано на рисунках: Г - образное Симметричное Симметричное полузвено Т - образное звено П - образное звено Рассмотрим условия фильтрации для Г- образного полузвена. Условия фильтрации для реактивных четырехполюсников   Определим условия, при которых реактивный четырехполюсник (четырехполюсник без потерь) будет электрическим ...

Расчет и анализ фильтров лестничной структуры

Скачать

11535

0

11

... AS - затухание в полосе задерживания, дБ, DА - неравномерность частотной характеристики в полосе пропускания, дБ, L – индуктивность, С – емкость, Задание на курсовую работу. Рассчитать и проанализировать пассивный фильтр лестничной структуры. Тип фильтра - ФВЧ Кауэра (эллиптический). Надо спроектировать фильтр в виде реактивного четырехполюсника лестничной структуры с нагрузкой на входе и ...