Навигация
Метод разложения случайного процесса на фазы (метод псевдосостояний)
1. Метод разложения случайного процесса на фазы (метод псевдосостояний)
2. Метод вложенных цепей Маркова
Метод псевдосостояний
Суть метода состоит в том, что состояния системы, потоки переходов из которых являются немарковскими, заменяются эквивалентной группой фиктивных состояний, потоки переходов из которых являются марковскими.
Условие статистической эквивалентности реального состояния и соответствующих ему фиктивных состояний в каждом конкретном случае выбирается по-разному. В качестве одного из критериев эквивалентности можно принять следующее условие:
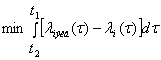
, где li экв(t) – эквивалентная интенсивность перехода в i-той группе переходов, заменяемой реальный переход обладающей интенсивностью li(t).
За счет расширения числа состояний системы, некоторые процессы удается точно свести к марковским. Созданная таким образом новая система по своим характеристикам статистически эквивалентна или близка реальной системе, но она должна быть обязательно подвергнута обычному исследованию на адекватность, с помощью хорошо проработанного математического аппарата с использованием уравнений Колмогорова.
К числу процессов, которые введением фиктивных состояний можно точно свести к марковским, относятся процессы, происходящие в системе под воздействием потока Эрланга.
В случае потока Эрланга k-го порядка интервал времени между сообщениями представляет собой сумму k независимых случайных интервалов распределенных по показательному закону. Поэтому сведение потока Эрланга k-го порядка к Пуассоновскому осуществляется введением k псевдосостояний. Интенсивности перехода между псевдосостояниями равны соответствующему параметру потока Эрланга.
Полученная таким образом эквивалентный случайный процесс является марковским, т.к. интервалы времени нахождения его в различных состояниях подчинены показательному закону распределения.
Пример.
Некоторое устройство S выходит из строя с интенсивностью l, причем поток отказов Пуассоновский. После отказа устройство восстанавливается. Время восстановления распределено по закону Эрланга 3-го порядка с функцией плотности![]() . Найти предельные вероятности возможных состояний системы.
. Найти предельные вероятности возможных состояний системы.
Система S может принимать два состояния:
S0 – устройство исправно
|

|
|
|
Представим случайное время восстановления в виде суммы 3х интервалов, распределенных по показательному закону с интенсивностью m:
![]()
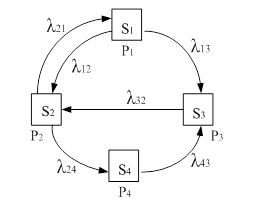
S1 заменяем эквивалентной цепочкой из трех псевдосостояний.
|

|
|
|
|
|

|

|


Последние 2 уравнения являются условием нормировки и условием эквивалентности замены состояния S1 псевдосостояниями.
Метод вложенных цепей Маркова.
Вложенные марковские цепи образуются следующим образом: в исходном случайном процессе выбираются такие моменты времени tk, в которых значения характеристик процесса образует марковскую цепь. Моменты времени tk обычно являются случайными и зависят от свойств самого процесса. Исходный процесс исследуется в выбранные моменты времени с помощью стандартных методов теории массового обслуживания.
Частным случаем вложенных цепей Маркова, являются полумарковские случайные процессы. Случайный процесс с конечным или счетным множеством состояний называется полумарковским, если заданны вероятности перехода системы из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t))
Классификация систем массового обслуживания
В общем случае СМО классифицируется по следующим признакам:
· закону распределения входного потока
· числу обслуживающих приборов
· закону распределения времени обслуживания в обслуживающих приборах
· числу мест в очереди
· дисциплине обслуживания
При определении любой системы обслуживания для сокращенной записи используется следующая система кодировки, в которой на месте букв ставится соответствующая характеристика СМО:
A | B | C | D | E| A | Закон распределения интервалов времени между поступлением заявок. | M – экспоненциальный E – Эрланга H – гиперэкспоненциальный Г – гамма-распределение D – детерминированное распределение G – произвольное распределение |
| B | Закон распределения времени обслуживания в приборах СМО. | |
| C | Число обслуживающих приборов. | 1 – для одноканальных систем l – для многоканальных систем |
| D | Число мест в очереди. Если число мест не ограничено, то поле можно опустить. | r либо n – для конечного числа мест |
| E | Дисциплина обслуживания. По умолчанию LIFO – в этом случае поле может опускаться. | FIFO, LIFO, RANDOM |
Примеры.
M | M | 1
СМО с одним обслуживающим прибором, бесконечной очередью, экспоненциальным законом распределения интервалов времени между поступлением заявок и временем обслуживания и дисциплиной обслуживания FIFO.
E | H | l | r | LIFO
CМО с несколькими обслуживающими приборами, конечной очередью, законом распределения Эрланга интервалов между поступлением заявок, гиперэкспоненциальным законом распределения времени обслуживания заявок в приборах и дисциплиной обслуживания LIFO.
G | G | lСМО с несколькими приборами, бесконечной очередью, произвольными законами распределения времени между поступлением заявок и времени обслуживания, FIFO.
Для моделирования вычислительной системы наиболее часто используются следующие типы СМО:
1. Одноканальная СМО с ожиданием.
· один обслуживающий прибор с бесконечной очередью
· является наиболее распространенной при моделировании
· может заменить практически любой узел вычислительной системы или ЛВС
2. Одноканальная СМО с потерями.
· один обслуживающий прибор с конечным числом мест в очереди
· если число заявок превышает число мест в очереди, то лишние заявки теряются
· используется при моделировании каналов передач данных в ВС и ЛВС
3. Многоканальная СМО с ожиданием.
· несколько параллельно работающих обслуживающих приборов с общей бесконечной очередью
· используется при моделировании групп абонентских терминалов, работающих в диалоговом режиме
4. Многоканальная СМО с потерями.
· несколько параллельно работающих обслуживающих приборов с общей очередью, число мест в которой ограничено
· часто используется, как и (2), при исследовании каналов связи
5. Одноканальная СМО с групповым поступлением заявок
· один обслуживающий прибор с бесконечной очередью
· перед обслуживанием заявки группируются в пакеты по определенном признаку или правилам
· используется для моделирования центров коммутации
Похожие работы
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
... 6. Петухов О.А. , Морозов А.В. , Петухова Е.О. Моделирование системное, имитационное, аналитическое. Учебное пособие – Санкт-Петербург 2008 7. Норенков И.П., Федорук Е.В.Имитационное моделирование систем массового обслуживания. Методические указания – Москва 1999 8. Кутузов О.И., Татарникова Т.М., Петров К.О. Распределенные информационные системы управления. Учебное пособие – Санкт-Петербург ...
... *0,1*25 – 1*,09 = 2148,2 ден.ед. Таким образом, максимальная прибыль достигается при установлении трех телефонных линий. Программа имитационного моделирования для оптимального режима работы примет вид: имитационный моделирование массовый обслуживание Результаты расчетов функциональных характеристик СМО: Характеристика Значение l 1/0,67 = 1,5 зв./мин. m 60/2=30 зв./мин. ...
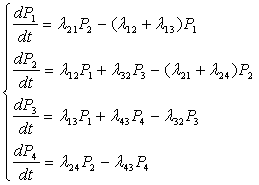

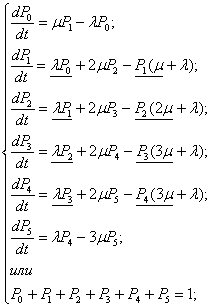




0 комментариев