Расчет длины регенерационного участка

8.3 Расчет длины регенерационного участка

8.3.1 Расчет количества и помехоустойчивости линейных регенераторов

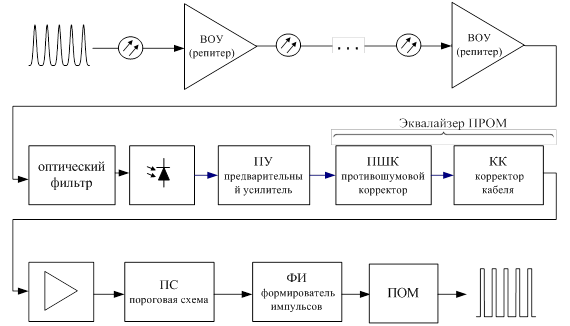
Рис.8.4 Блок схема линейного регенератора (РЛ)

Характеристики линейного регенератора:

·  Энергетический бюджет:

, (1)

где a[дБ/км], L - затухание и длина ОВ, P_ПОМ, P_min – пиковая мощность световых импульсов на выходе ПОМ и чувствительность ПРОМ соответственно.

·  Скоростной бюджет ВОСП

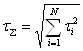(2)

где τ_i – быстродействие отдельных компонент ВОСП;   - общее быстродействие системы.

В случае NRZ – кода допустимое время нарастания и спада  может достигать 70% от периода, т.е.:

, (3)

где B – битовая скорость. Для бифазных кодов:

. (4)

Составляющими суммы в (2) являются:

- быстродействие ПОМ и его контроллера τ_пом;

- быстродействие ПРОМ τ_пром; - быстродействие ОК:

; , (5)

где D- коэффициент хроматической дисперсии ОВ;  - уширение оптического сигнала, связанное с межмодовой дисперсией в многомодовом ОВ; - полоса частот ОВ длиной 1км., которая является справочной величиной.

·  В условиях, когда чувствительность РЛ определяется тепловым шумом с гауссовой статистикой его коэффициент битовых ошибок p_ош определяется формулой:

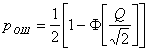, (6)

где Ф(х)- табулированная функция ошибок

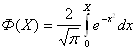(7)

·  Распространенная аппроксимация функции ошибок:

, (8)

·  Величина p_ош полностью определяется Q-фактором помехоустойчивости ЦСП:

, (9)

где U₁, U₀ - средние уровни напряжений на выходе фотоприемника на тактовых интервалах (ТИ) длительностью  при передаче 1 и 0 соответственно; s₁ и s₀ - среднеквадратичные уровни шумовых напряжений на указанных ТИ.

·  Выражение (9) справедливо, если пороговый уровень U_пор решающего устройства ПРОМ установлен равным:

. (10)

·  Параметры U₁, U_0, s₁ и s₀ в выражении для Q-фактора шумящего ПУ можно выразить через соотношение чисел сигнальных и шумовых фотоэлектронов на анализируемом ТИ:

(11)

где n_c- среднее число сигнальных фотоэлектронов на ТИ:

(12)

, M, F(M)- квантовая эффективность коэффициент лавинного умножения и коэффициент шума лавинного ФД; Для p-i-n диода F(M)=1. Для ЛФД: , где:

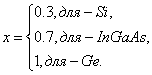(13)

- мощность оптического сигнала;  Дж/Гц – постоянная Планка;

(14)

- среднее число фотоэлектронов темнового тока ФД на ТИ, определяющее его дробовой шум;

Кл – заряд электрона; T – длительность ТИ;

G- суммарный коэффициент шума репитеров (ВОУ) регенерационного участка длиной L,

(15)

где - расстояние между репитерами (ВОУ); - коэффициент затухания сигнала в ОВ;

- коэффициент инверсии ВОУ, определяющий его шумовые свойства.

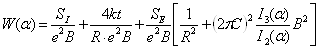(16)

безразмерный температурный параметр, определяющий уровень шумов входной цепи и усилителя ПРОМ;

t – температура в градусах Кельвина;  Дж/К – постоянная Больцмана; где ,- шумовые параметры транзисторов (см. ниже).

Величина R в (16) определяет номинал нагрузочного резистора интегрирующего ПУ или сопротивления обратной связи ТИУ. Емкость же C складывается из выходной емкости фотодиода, входной емкости ПУ и емкости монтажа.

В формуле (16) коэффициенты I₂,I₃ в, называемые интегралами Персоника, устанавливают соотношение между эффективной шумовой полосой частот ПУ В_эф и битовой скоростью B:

. (17)

При этом второе слагаемое (17) определяет уширение В_эф, связанное с воздействием на помехоустойчивость ПРОМ внутреннего источника шумового напряжения  предварительного усилителя ПРОМ (см.рис.6). Коэффициенты I₂,I₃ выражается через отношение спектров огибающей оптического сигнала на выходе () и входе () ПУ. Аргументом этих зависимостей является безразмерная нормированная частота :

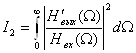, (18)

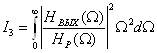 (19)

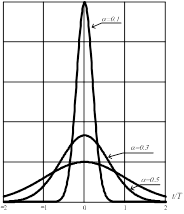
·  Спектр  в (18),(19) определяется формой оптического сигнала на входе ПРОМ Р_с(t), которая чаще всего близка к гауссовой кривой:

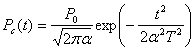. (20)

где a- параметр формы сигнала (см. рис.2). Вследствие частотных ограничений АЧХ линейного тракта H(f) сигнал Р_с(t) на выходе ПРОМ отличается от (20). Обычно указанные отклонения используют для минимизации межсимвольной интерференции. Именно этим условием и регламентируется форма АЧХ H(f) цифрового ПРОМ.

·  Таким свойством, например, обладает тракт с характеристикой H(f) вида «приподнятого косинуса»:

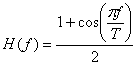, (21)

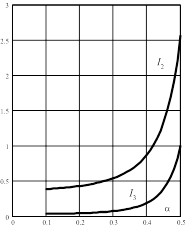
которая получила широкое распространение на практике. Для сигналов гауссовой формы и АЧХ вида (3) зависимость интегралов Персоника I₂,I₃ от параметра формы гауссового сигнала a изображена на рис.8.6.

·  Важной характеристикой ЛР является входящий в формулу (10) коэффициент уширения сигнала g относительно длительности ТИ. Он описывает дисперсионные искажения цифрового сигнала в ОВ и численно равен доле сигнальных фотоэлектронов рассеянных за пределы «своего» ТИ. Эта доля и определяет дисперсионное уширение импульса на величину :

. (22)

Для сигналов гауссовой формы рассчитанная по зависимость параметра g от a изображена на рис.8.8.

·  В одномодовых оптических волокнах (ОВ):

, (23)

где  - дисперсионный коэффициент ОВ; L – длина линии связи;  - ширина спектра оптического сигнала.

Значения коэффициента D стандартизировано требованиями МСЭ-Т (ITU-T) и соответствует данным рисунка 4. Здесь используются обозначения: DSF (Dispersion Shift Fiber)- ОВ со смещенной дисперсией; NDSF (Non Dispersion Shift Fiber) – стандартное волокно с несмещенной дисперсией; NZ-DSF (Non Zero Dispersion Shift Fiber) – волокно с ненулевой смещенной дисперсией.

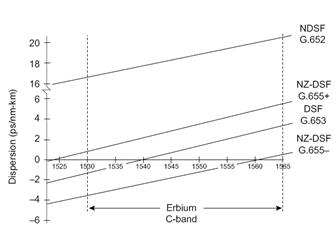
Рис.8.7 Требования на уровень дисперсии в ОВ различного типа

·  Для многомодового ОВ со ступенчатым профилем:

, (24)

где - разность показателей преломления сердцевины и оболочки  ОВ:

 , (25)

NA – числовая апертура ОВ; - параметр связи мод (если связи нет, то; полная связь- ).

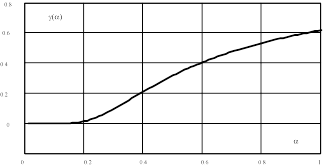
Рис.8.8. Зависимость коэффициента уширения g от параметра a сигнала гауссовой формы

·  Для многомодового градиентного ОВ:

. (26)

·  Теоретическое ограничение на минимальную ширину линии излучения лазера  в (23). Если излучение идеального лазера () модулируется со высокой скоростью B, то линия излучения уширяется на величину:

.

Откуда, учитывая, что , получим:

. (27)

Из (27) следует, что уширение линии излучения, связанное с модуляцией ЛД, при скорости B~10 Гбит/с превышает ширину спектра немодулированного излучения DBF – лазера и этот эффект следует учитывать при расчете МСИ-1.